几千年来，人类就使用纽结。比如世界著名的中国结，起源于唐宋时期（公元 960-1279 年），在明代就得到普及。

纽结理论，或结理论，是研究纽结的代数拓扑特性一个数学分支，它不只是一种抽象的数学形式，它推动了数学和其他领域的许多发现。科学家们利用结理论来研究流体力学、电动力学，它们的特性可以帮助解开隐藏在DNA中的生物化学、新材料的合成、三维空间几何，等广泛课题中的奥秘。

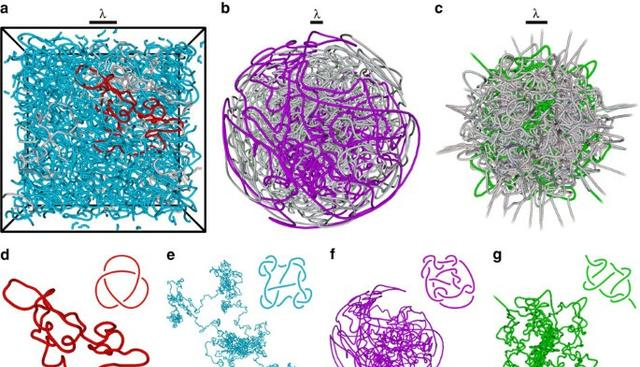
但人类并不是唯一一种认知纽结的，有些生物在纽结方面做的更好，而且在解纽结方面也更胜一筹，解纽结速度相当的快。科学家们一直在研究为什么它们具有这样的特异功能。

譬如，科学家们在实验室研究了一种加州蠕虫 (学名：Lumbriculus variegatus)，一种可以长到10 公分长的细线虫。成千上万的蠕虫可以错综复杂地纠缠在一起，以适应自然环境的需要。了不起的是，这些蠕虫可以在几分钟内紧紧缠绕抱成一团，但它们又可以在短短的几个毫秒的“一眨眼”时间里，“瞬间”快速解开缠结疏散开来，以摆脱捕食者的威胁。

现在，麻省理工学院和佐治亚理工学院的数学家们开发出了一种新型的数学模型，解决了这种快速纽结与快速解结的数学与力学的机理问题。该研究结果发表在最近一期的《科学》杂志上。

科学家们想认知这些蠕虫是如何组成纽结与改变纽结的动力学机制及其背后的具体机理。重要的是，这些缠结不是典型的、静态的纽结，譬如我们通常所熟悉的绳结，它们使我们的鞋穿在脚上，使船固定在码头上，使登山者避开危险。科学家们现在想要探索的是非平衡状态的、活生生的、动态的缠结，这为纽结问题更增添了一层迷人的色彩。而且我们知道，纽结容易解结难。加州蠕虫的这种超快速的解结能力更使科学家着迷。

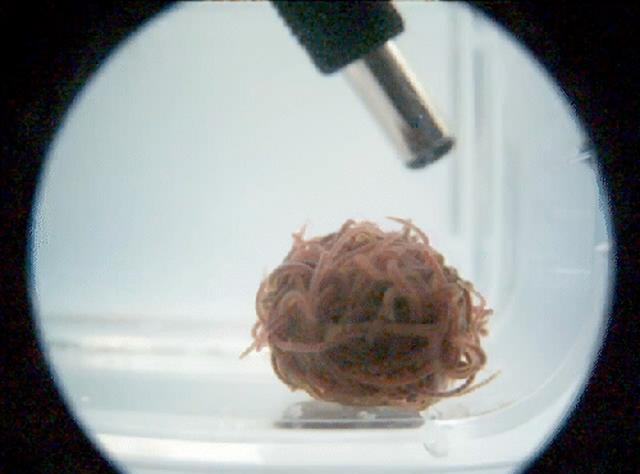
为了激发蠕虫的这种逃避反应，研究人员用紫外线照射蠕虫团群，导致它们“爆炸性地”散开来。但仍然了解不了球团中心所发生的机制。为此，他们将一团活的蠕虫放入无毒的果冻中，用超声波机从内部观察这种现象。将这些超声波图像组合成电影，绘制了近5万个数据点以了解“运动背后的数学原理”，并创建了一个数学模型，可以帮助预测每条蠕虫的确切逃生路径。

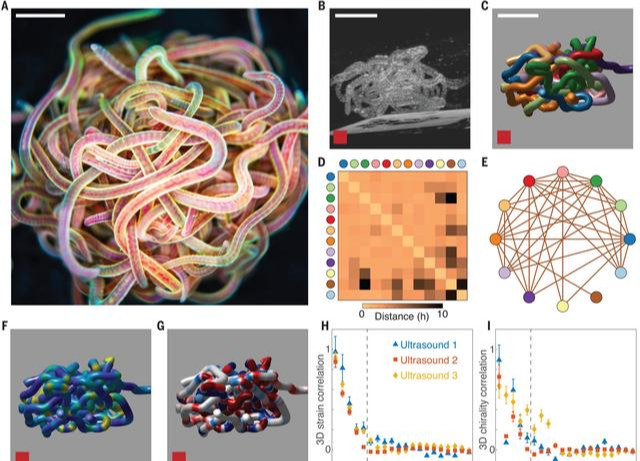
回答蠕虫如何快速解开缠结的问题需要结合力学和拓扑学。研究表明，这是一种相当无序与复杂的结构，但这些活的蠕虫结构能够操纵这些结以实现所需要的关键功能。

该模型预测，每条蠕虫都会与至少两条其他蠕虫交织在一起，然后它们会在需要解开时使用“螺旋波动运动”，就像开瓶器一样旋转它们的身体。科学家们不仅认知了蠕虫以这种方式移动，该研究还表明了它们为何使用这些快速移动的方式，首次建立起一种主动纽结和解开纽结的数学理论，研究人员认为这种理论将可以应用于其他许多领域。