八
下

八下数学 | 期中必考题型
【构造中位线】5种常用方法
方法一
倍长法构造三角形的中位线
如图,在△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M为AF的中点,求证:ME=1/2CF.

证明:如图,延长FE至N,使EN=EF,连接BN,AN.易得ME=1/2AN.
∵EF=EN,∠BEF=90°,
∴BE垂直平分FN.∴BF=BN.
∴∠BNF=∠BFN.
∵△BEF为等腰直角三角形,∠BEF=90°,
∴∠BFN=45°.∴∠BNF=45°,
∴∠FBN=90°,即∠FBA+∠ABN=90°.
又∵∠FBA+∠CBF=90°,
∴∠CBF=∠ABN.
在△BCF和△BAN中,

∴△BCF≌△BAN.
∴CF=AN. ∴ME=1/2AN=1/2CF.
方法二
已知一边中点,取另一边中点构造三角形中位线
如图,在△ABC中,∠C=90°,CA=CB,E,F分别为CA,CB上一点,CE=CF,M,N分别为AF,BE的中点,求证:AE=MN.

证明:如图,取AB的中点H,连接MH,NH,则MH=1/2BF,NH=1/2AE.
∵CE=CF,CA=CB,
∴AE=BF.
∴MH=NH.
∵点M,H,N分别为AF,AB,BE的中点,
∴MH∥BF,NH∥AE.
∴∠AHM=∠ABC,∠BHN=∠BAC.
∴∠MHN=180°-(∠AHM+∠BHN)
=180°-(∠ABC+∠BAC)=90°.
∴NH=√2/2MN.
∴AE=2NH=2×√2/2MN=√2MN.
方法三
利用角平分线+垂直构造中位线
如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,点E为BC的中点,求DE的长.

解:如图,延长BD交AC于点F,
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵BD⊥AD,∴∠ADB=∠ADF,
又∵AD=AD,∴△ADB≌△ADF(ASA).
∴AF=AB=6,BD=FD.
∵AC=10,∴CF=AC-AF=10-6=4.
∵E为BC的中点,∴DE是△BCF的中位线.
∴DE=1/2CF=1/2×4=2.
方法四
连接两点构造三角形的中位线
如图,点B为AC上一点,分别以AB,BC为边在AC同侧作等边三角形ABD和等边三角形BCE,点P,M,N分别为AC,AD,CE的中点.
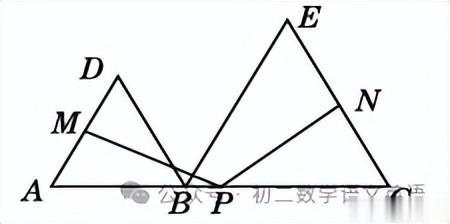
(1)求证:PM=PN;
证明:如图,连接CD,AE.
由三角形中位线定理可得PM綊1/2CD,PN綊1/2AE.
∵△ABD和△BCE是等边三角形,
∴AB=DB,BE=BC,∠ABD=∠CBE=60°,
∴∠ABE=∠DBC.
∴△ABE≌△DBC,∴AE=DC.
∴PM=PN.

(2)求∠MPN的度数.
解:如图,设PM交AE于F,PN交CD于G,AE交CD于H.由(1)知△ABE≌△DBC,
∴∠BAE=∠BDC.
∴∠AHD=∠ABD=60°,
∴∠FHG=120°.
易证四边形PFHG为平行四边形,
∴∠MPN=120°.
方法五
已知两边中点取第三边中点构造三角形的中位线
如图,在△ABC中,AB=AC,AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N,求证:AN=1/3AC.

证明:如图,取NC的中点H,连接DH,
过点H作HE∥AD,交BN的延长线于E.
∵AB=AC,AD⊥BC,
∴D为BC的中点.
又∵H为NC的中点,
∴DH∥BN.
又∵PD∥EH,∴四边形PDHE是平行四边形.
∴HE=PD.又∵P为AD的中点,
∴AP=PD.∴AP=EH,
易证△APN≌△HEN,∴AN=NH.
∴AN=NH=HC,
∴AN=1/3AC.

