问题:
计算:sin²3°+cos²27°-sin3°*cos27°的值。
主要内容:
通过三角函数的诱导公式、30°角和60°角三角函数特殊值、倍角公式,以及三角函数和差化积公式、积化和差公式和图形分析计算法,介绍计算三角代数式sin²3°+cos²27°-sin3°*cos27°值的主要步骤。
主要公式:
和差化积:sina-sinb=2cos[(a+b)/2]*sin[(a-b)/2];
积化和差:cosa*cosb=(1/2)*[cos(a+b)+cos(a-b)]。
※.三角函数计算法:
sin²3°+cos²27°-sin3°*cos27°
=sin²3°+cos27°*(cos27°-sin3°),提取公因式cosa12;
=sin²3°+cos27°*(sin63°-sin3°),
诱导公式应用sina=cos(90º-a);
=sin²3°+cos27°*2cos33°sin30°,
使用和差化积公式sina-sinb=2cos[(a+b)/2]*sin[(a-b)/2];
=sin²3°+cos27°*cos33°,代入三角函数值sin30°=1/2;
=sin²3°+(1/2)[cos(27°+33°,)+cos(33°-27°),
使用积化和差公式cosa*cosb=(1/2)*[cos(a+b)+cos(a-b)];
=sin²3°+(1/2)(cos60°+cos6°),
=sin²3°+1/4+(1/2)cos6°,
=sin²3°+1/4+(1/2)(2cos²3°-1),使用倍角公式cos2a=2cos²a-1,
=sin²3°+cos²3°+1/4-1/2,使用平方和公式sin²a+cos²a=1,
=1-1/4=3/4.
※.图形结合计算法
如下图,构建直角三角形ABC,D是直角边BC上的一点,且∠ADB=30°,设∠DAB=z=3°,则∠ABC=30°-z=27°角。设斜边的长度为单位长度1,BD的长度为x。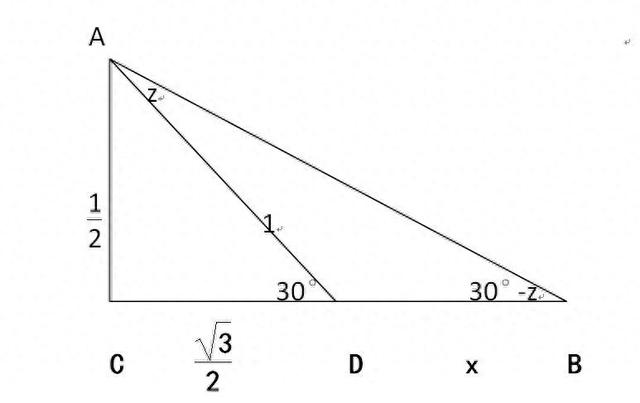
在Rt△ACD中:∠ADC=30°,所以AC=1/2,CD=√3/2,
在Rt△ACB中:由勾股定理可知AB的长为:
AB=√[(1/2)²+(√3/2+x)²]=√(x²+√3x+1)。
在△ADB中,由正弦定理可知:
BD/sinz=AB/sin∠ADB,即:
sinz=sin7°=xsin150°/AB=x/2AB,
在Rt△ABC中,有:
cos(30°-z)=cos23°=BC/AB=(√3+2 x)/2AB,所以:
sin²7°+cos²23°-sin7°*cos23°
=(x/2AB)²+ [(√3+2x)/2AB]²- (x/2AB)* [(√3+2 x)/2AB],
=[x²+ (√3+2x)²- x (√3+2x)]/4AB²,
=[x²+ (√3+2x)²- x (√3+2 x)]/4AB²,
=3(x²+√3x+1)/[4*(x²+√3x+1)]
=3/4.
※.问题小结:
本题可以推广计算:
sin²z°+cos²(30-z°)-sinz°*cos(30°-z°)=3/4.
