
引用
Kalhauge, Christian Gram and J. Palsberg. “Logical bytecode reduction.” Proceedings of the 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation (2021): n. pag.
摘要
将导致错误的输入转换成更小的输入对于具有内部依赖性的输入是有挑战性的,因为大部分子输入是无效的。Kalhauge 和 Palsberg 在这个问题上取得了进展,他们将任务映射为依赖图的约减问题,完全避免了无效输入。他们的工具 J-Reduce 有效地将 Java 字节码减少到原来大小的 24%,这使得它成为迄今为止最有效的工具。然而,由 J-Reduce 约减得到的输出结果的体量通常还是过大,无法有效地辅助 Bug(缺陷)报告的生成。对错误报告没有帮助。在本文中,我们展示了更细粒度的依赖建模,该方法带来了更多的约减。具体来说,我们使用命题逻辑来指定依赖关系,并展示了这如何适用于 Java 字节码。一旦我们有了指定所有有效子输入的命题公式,我们就运行一个算法来找到一个小的、有效的、导致失败的输入。我们的算法交错运行有问题的程序,并调用找到最小满意赋值的程序。我们的实验表明,我们可以将 Java 字节码减少到其原始大小的 4.6%,这比 J-Reduce 实现的 24.3%要好 5.3 倍。小得多的输出更适合 bug 报告。
1.介绍
假设我们现在有一组可能导致目标程序失败的输入,该输入是有效的,因此目标程序会执行这一组输入;然而,输入的数据以及数据的类型是是众多的,以至于在出现错误时我们无法准确的确定 bug 的性质。由 Zeller 和 Hildebrandt 首先提出输入约减过程,通过找到一个重现故障的小输入来解决这个问题。他们的算法 ddmin 产生一个子输入来重现失败。他们发现在子输入上运行会有三种结果:失败仍然发生,失败已经消失和不知道。“不知道”结果发生在子输入无效时,尽管原始输入有效。正如 Regehr 等人所指出的,无效的子输入对发现错误没有任何帮助。
Java 字节码在约减方面存在着一定的难度。对于 C 来说,测试用例有效性问题中最具挑战性的部分是动态无效的程序。C-Reduce 通过使用语义检查 C 解释器来动态检测无效输入来解决这个问题。对于 Java 字节码来说,最大的挑战是许多内部依赖。J-Reduce 通过创建一个完全避免静态无效输入的依赖图来解决这个问题。因此,C 和 Java 的约减问题是不同的。我们将展示,对内部依赖关系进行更详细的建模可以使 Java 字节码约减更加有效。

图 1 当 M.x()、M.main()和 A.m()同时出现时,在工具中产生错误的示例输入程序。第二个子图是保留 bug 的最优优化。为了简洁起见,我们将代码以…省略。
2.依赖关系建模
我们将阐述我们如何进行依赖关系建模,我们将讨论我们的实现中超出传统模型的方面。
使用接口的轻量级 Java。带有接口的轻量级 Java(FJI)是轻量级 Java 的适度扩展:每个类实现一个单一接口。接口由一组签名组成。虽然我们可以用图约束来建模轻量级 Java 的依赖关系,但是我们需要 FJI 命题逻辑的全部能力。
我们将为 FJI 定义语法和类型系统,以及一个约减器。从一个程序中,我们生成对内部依赖关系建模的约束,然后我们解决约束,最后我们将解决方案反馈给一个约减器。其思想是,对于任何解决方案,约减程序类型检查。

图 2 包含语法(实线、黑色)和引用(虚线、灰色)依赖关系的依赖关系图。我们已经将代码变量缩写为[code]。我们从 M 开始给最小闭包的变量部分涂上阴影。

图 3:使用接口的轻量级 Java 的语法(FJI)
语法。图 3 显示了 FJI 的语法。具体细节参照 Atsushi Igarashi, Benjamin Pierce, and Philip Wadler. 1999. Featherweight Java: A Minimal Core Calculus for Java and GJ. In Proceedings of the Conference on Object-Oriented Programming, Systems, Languages,and Applications. 132–146.
图 5 和图 6 显示了 FJI 的帮助规则和类型规则。在类型规则中,我们使用 Γ 来覆盖类型环境,即从标识符到类型的映射。我们使用 π,σ 来覆盖逻辑公式。我们用缩写 π = π1 ∧...∧πn。我们用 P(C)来表示 P 中名为 C 的类,用 P(I)来表示 P 中名为 I 的接口。对于每个 P,我们假设:


图 4:FJI 帮助规则 图 5:FJI 类型改规则
类型规则规定了程序类型检查的条件。当 p 满足这些条件时,我们写出 ⊢ P | π。下面我们解释 π 的作用。
布尔变量和程序约减器。对于一个给定的程序,我们定义了一组将被约束使用的布尔变量。然后我们定义一个约减器,给定一个解决约束的约减器,将一个程序映射到一个约减的程序。
从程序 P 中,我们导出了一组布尔变量,我们称之为 V(P)。我们使用 ϕ 作为变量的真值赋值,以在 V(P)→Bool 范围内。想法是,ϕ([C])=1,那么约减器应该保持 C 类,否则将其移除。我们有六种变量:[C]切换 C 类,[I]切换接口 I,[C.m()]切换 C 中的方法 C.m,[I.m()]切换 I 中的签名 I.m。变量[C◁I]表示我们是否应该保持 C 实现 I 或者我们可以将 C 实现空接口(EmptyInterface)。最后,变量[C.m()!code]表示我们是否应该保留 C.m()方法的主体。否则,我们可以用一个微不足道的部分来代替它。
图 6 中的约减器实现了上面解释的布尔变量的思想。这个约减器构成了我们实现 Java 字节码的核心。对于任何映射 ϕ : V(P) →Bool ,我们构造一个约减程序 reduce(P,ϕ)。

图 6:FJI 的约减函数
生成类型检查约束。图 4 和 5 显示了类型规则。对于程序 p,我们编写 ⊢P|π 来表示我们同时键入 check P 并生成使用 V(P)中变量的命题公式 π。我们用符号 ϕ|=来表示 ϕ 满足 π。
图 4 中 FJI 的帮助规则很像轻量级 Java,但是有两个不同之处。第一个是我们扩展了方法类型查找来应用于接口,现在子类型规则生成了对类及其接口之间的连接进行建模的约束。第二个是一组新的方法选择规则。对于程序 P 中的类 C 和方法 m,约束 mAny(p,m,C)是变量的分离,所有变量的形式都是[C.m()]。如果我们需要 C 类在约减程序中实现一个方法 m,那么我们可以要求 mAny(p,m,c)为真。这将确保约减器至少保留一种这样的方法 m。
图 5 中 FJI 的类型规则类似于轻量级 Java 的类型规则,除了与接口和签名相关,以及约束生成的新规则。
定理 2.1。

Java字节码。我们已经为 Java 字节码实现了一个约减器和一个约束生成器,其中我们的 FJI 模型是核心。我们总共有 11 项可以移除,包括构造函数、字段和超类关系。在约束生成过程中需要特别注意的构造包括抽象类、扩展其他接口的接口、实现多个接口的类以及类型转换。此外,我们必须对 Java 泛型和类型推理进行建模。使用 Java 泛型的类型检查是不可判定 的,我们的方法将类型检查问题近似为约束的一部分,因此不可判定性是我们的一个限制因素。我们设计了一个在实验中运行良好的近似值。特别是,到目前为止,Java 泛型模型从未导致我们的工具产生无效的子输入。
3.逻辑约减
在本节中,我们将使用逻辑重述“输入约减问题”,并展示广义二元约减算法如何使我们能够有效地减少输入。
3.1 注释
我们用小写字母表示变量 v,大写字母表示集合 L。D,L 表示集合的集合。2X 表示集合 X 的幂集。在列表中,我们可以用下标 Dn 访问第 n 个元素。
解 M 是对逻辑语句 R 的一个成功的赋值,我们把它写成 R(M)。我们把解写成真实变量的集合。例如(x∧ ¬ y)({x})为真,(x∧ ¬ y)({x,y})为假。我们还可以得到逻辑语句的变量 VARS(R)。我们还可以调节或更新逻辑表达式(R|x=1,y=1),这有效地替代了 R 中的 x=1 和 y=1。这也适用于集合(R|X=1)。
合取范式(CNF)是使用子句的合取来表示逻辑表达式。子句是文字的析取,术语是文字的合取。文字是一个普通的或否定的变量。我们定义了以下简记法:

3.2 问题形式化
首先,我们将输入表示为一组变量 I,将子输入表示为 I 的子集。在第 2 节中,这个集合 I 被称为 V(P),每个子输入由定义在 V(P)上的真值赋值 ϕ 表示。我们将可能有 bug 的程序表示为黑盒谓词 P,当且仅当子输入导致工具中出现 bug 时,该谓词在子输入上为真。黑盒的概念意味着我们可以在 I 的子集上调用 P,但是我们不能以任何其他方式检查 P。黑盒谓词模型的概念是,我们必须运行工具来了解它。最后,我们得到了 I 上的命题布尔公式 RI。在第 3 节中,这个由输入生成公式 RI 被称为 σ。
定义 3.1(输入约减问题)。实例:(I,P,RI,k),其中 I 是一组变量,P 是 I 子集上的黑盒谓词,RI 是 CNF 在 I 中的布尔公式,k 是表示最大成本的整数。
假设:p 可以在多项式时间内计算,P(I)和 RI(I)都为真,p 在有效子区间上是单调的:如果 X⊆Y 并且 RI(X)和 RI(Y)为真,那么 p(x)=>p(y)。
问题:决定 ∃S⊆I:P(S)∧RI(S)∧|S|<k。
我们对输入有效性进行建模,并且我们要求 P 在有效子输入上是单调的,并且在子输出上没有代价函数。然而,三个输入约减问题因不能用多项式算法而使问题无法解决的,出于同样的原因:我们可以很容易地将命中集问题(因不能用多项式算法而使问题无法解决的)约减为每个输入约减问题。
定义 3.2:输入约减问题时因不能用多项式算法而使问题无法解决的。
在本节的剩余部分,我们将重点关注输入约减问题的优化版本。具体来说,我们将提出多项式时间算法,每个算法都找到(I,P,RI)的小解。
3.3 广义二元约减法
广义二元约减法(GBR,算法 1)在多项式时间内近似解决输入约减问题。GBR 使用两个构造块:评估黑盒谓词 P 和计算近似最小满意赋值(MSA)。我们定义最小意味着 MSA 给尽可能少的变量赋值为真,这是一个因不能用多项式算法而使问题无法解决的问题,所以我们解决了一个近似解。GBR 学习 P 和 MSA 的调用结果,这使它能够为以后的调用选择好的输入。
主要算法。GBR 用产生一系列有效输入的子程序 PROGRESSION 来扩展二元约减。progression 是一个列表,其中每个前缀代表一个有效的输入。GBR 只将黑盒谓词 P 应用于列表的前缀,因此只应用于有效的输入。
GBR 维护三个数据结构。首先,变量 order⪯(I 内的 order 总数),这有助于主循环在多项式时间内终止;它也有助于我们设计 MSA 在多项式时间内终止。第二,当前的列表 D 代表当前的搜索空间。搜索空间满足黑盒谓词 P,D 将搜索空间划分为非空的不相交的列表子集。第三,L 中学习到的集合是关于 p 增长的知识。主循环保持每个学习集既与满足 P 的每个有效子输入重叠,又与列表的每个前缀重叠。

引理 3.3(不变性)GBR 在(I,P,RI)上的主循环具有不变的 Inv(L, D):
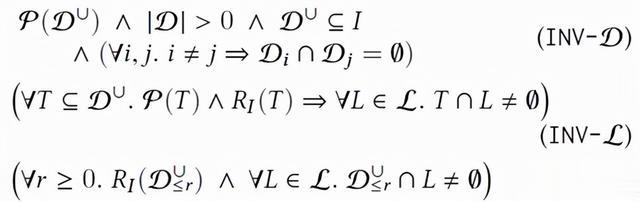
主循环的思想是我们对 P 学习的越多,那么我们找到满足 p 的有效输入的可能性就越大。主循环检查列表中的第一个集合 D0 是否满足 P。如果 D0 确实满足 P,那么主循环返回它,否则,主循环执行一下三个步骤。
首先,主循环找到满足 P 的列表的最小前缀
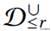
。这样的前缀之所以存在,是因为整个列表满足 P,我们可以通过二分搜索法有效地找到它。
第二,主循环将前缀的最后一组 Dr 集合添加到 L。由于 P 是单调的,Dr 是满足 P 的 D 的最短前缀,因此 Dr 中至少有一个元素必须是当前搜索空间内任何解的一部分。所以,添加 Dr 到 L 中。这个集合 Dr 对 L 来说是新的,经过几个步骤的推理后我们可以看到。之后,D0 与 L 中的所有集合重叠,Dr 必须在 L 中的每个集合中至少缺少一个元素。
第三,我们用 L 和
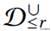
建立一个新的列表。
引理 3.4 GBR 可以在多项式时间内找到输入约减问题的近似解。
4.实验评估
本节将回答以下实验问题:在实践中,使用命题逻辑来建模内部依赖关系是否会有效地减少复杂的输入?
答案:是的!我们的工具将 Java 字节码减少到原来大小的 4.6%,比 J-Reduce 实现的 24.3%好 5.3 倍。
实现:我们的实现和评估是作为 J-Reduce 的扩展而写的。我们的逻辑模型建立在一个 Haskell eDSL 中,大约有 800 行代码。
基准:我们使用来自 J-Reduce 的基准,它是来自 NJR 项目的 100 个程序的集合,以及三个反编译程序。我们已经从基准集中删除了四个基准。其中三个是因为他们没有进行类型检测。这在 J-Reduce 论文中不是问题,因为它没有检查程序的类型。第四个是标准库的副本,这给我们带来了问题。
分析:我们首先将 J-Reduce 与我们的约减器进行比较。我们绘制了三个指标中每一个的累积频率图:减少所花费的时间,以及数字类和剩余字节的最终相对大小,见图 7a。通过检查第一个图,我们可以看到 J-Reduce 在一个小时内完成了所有基准的运行,而对于一些基准,我们的约减器需要长达 10 个小时。然而,我们可以看到它在两个小时内完成了大多数(超过 95%)的基准测试。对于这额外的运行时间,我们得到了更多的约减。我们可以看到,在类中,我们将基准测试的一半减少到 10%以下,在字节中减少到 5%,其中 J-Reduce 只减少到 40%左右。
最长的执行时间源于反编译程序需要时间来执行,并且某些情况下有许多明显的错误。每一个 bug 都需要 GBR 进行单独搜索。我们的一个长时间运行的案例导致了许多不同的 bug 和 9207 个变量的约束,我们最终用 13 个步骤做了 73 次搜索。总的来说,这个案例让我们在 8 小时内运行了 951 次反编译和编译,平均每次耗时 33 秒。
我们可以看到,J-Reduce 和我们的约减器几何平均运行时间分别为 218.6s 和 680.7s,这意味着我们的约减器比 J-Reduce 慢 3.1 倍。我们 约减器的约减效果要更好:对于类的数量,我们可以减少到 8.4%,而 J-Reduce 得到 22.8%,对于字节,我们减少到 4.6%,而 J-Reduce 得到 24.3%。我们在类上的性能提高了 2.7 倍,在字节上提高了 5.3 倍。
然而,当我们有 10 个小时用来约减,这种比较才是公平的。更有可能的场景是,我们有一个固定的时间窗口,我们希望算法在该时间范围内尽可能约减。我们可以在执行过程中的任何时刻停止这两种算法,并使用最小的输入,直到错误产生。为了说明这一点,在图 7b,我们绘制了一段时间内的平均减少量。

a: 根据类的数量和字节的数量,花费的时间和相对最终大小的累积频率图。总的来说,数字越陡越好。圆点代表几何平均值。

b: 约减时间。显示线性次数上的优化,目标变小。
图 7:实验结果
5.结论
我们已经表明,使用命题逻辑来建模内部依赖关系可以有效地约减复杂的输入。我们通过用接口对轻量级 Java 的类型系统建模,证明约减的程序类型检查来做到这一点。此外,我们已经通过实验表明,该模型扩展到了完整的 Java,并且比以前的工作更接近 Java 模型。我们的多项式时间算法,广义二元约减方法,使得这个模型得到了 5.3 倍的更好的结果。这种改进很大程度上可以通过简单的有损编码来实现,然而我们发现完成“最后一英里”需要强大的算法。
致谢
本文由南京大学软件学院 2021 级硕士研究生张啸翻译转述。
