2.有界函数和无界函数

函数y=x²的图象总是在x轴的上方，就是说，函数值总不小于0.我们把具有这种特征的函数叫做有下界的函数。同样，y=-x²的图象总是在x轴的下方，就是说，函数值总不大于0.我们把具有这种特征的函数，叫做有上界的函数。

又如函数 y=x²-x+2的图象上各点都在直线 y=7/4的上方（图4.10)，它是一个有下界的函数；函数 y=3-4x-2x²的图象上各点都在直线 y=5的下方（图4.11)，它是一个有上界的函数。

一个既有上界又有下界的函数叫做有界函数．例如．图5.5是函数 y =√(25-x²)的图象。图象上各点都在直线 y=0和直线 y=5之间，它是一个有界函数．

图5.5

但是对于函数y=x³来说，我们就不能找到任何一条平行于x轴的直线，使函数y=x³的图象只在这条直线的上方或者下方。这个函数既不是有上界的函数，也不是有下界的函数．

一般地说，对于函数 f(x)，在它定义域里自变量x的每一个值，如果存在这样的数 M ，能够使不等式

f(x)< M （或者 f ( x )≤ M) (1)

成立，那末函数 f(x)叫做有上界的函数；如果存在这样的数 m ，能够使不等式

f(x)> m （或者 f(x)≥ m ) (2)

成立，那末函数 f(x）叫做有下界的函数；如果这两个不等式都能成立，就是

m<f(x)<M (或者m≤f(x)≤M) (3)

都成立，那么函数f(x)叫做有界函数；如果不存在这样的数M或m，能使不等式(1)或(2)成立，那么函数f(x)叫做无界函数。

注 这里可以看到，一个有界函数一定既是有上界的函数，又是有下界的函数，但是一个有上界(或者下界)的函数却不一定是有界函数。

例2. 证明函数

是有界函数。

【证明】函数的定义域是区间-5≤x≤5.

当x取这个区间里的任何一个值的时候，

0≤25-x²≤25.

∴ 0≤√(25-x²)≤5.

即

0≤y≤5.

所以这个函数是有界函数。

注 考察一个函数是不是有界函数，叫做研究函数的有界性。了解了一个函数是有界函数，或者是有下界(有上界)的函数，那么作函数的图象时，就知道它的图象一定在某两条平行于x轴的直线之间或者某一条平行于x轴的直线的上方(下方)。

习题 5.2(2)

1.证明：

(1)函数

是有下界的函数，但没有上界；［提示：只需证明y≥0］

(2)函数

是有上界的函数，但没有下界。

2.已知函数

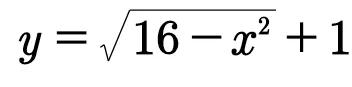
(1)求函数的定义域；

(2)求函数的值域；

(3)确定这个函数是不是奇函数或者偶函数；

(4)确定这个函数是不是有界函数。

初等函数的有界性

幂函数，指数函数，对数函数，三角函数和反三角函数这五类函数称为基本初等函数。

能用一个解析式表示，而且这个解析式是由常数和基本初等函数经过有限次的四则运算及有限次的复合所形成的函数，称为初等函数。

注意：由于分段函数不是用一个解析式表示的，所以它不是初等函数。

有界函数的符号定义

如果函数f(x)在它的定义域上，其绝对值|f(x)|的一切值都不大于某一个正数M时，就称这个函数为有界函数。即若|f(x)|≤M，则称函数f(x)为有界函数。

如果不论M是多么大的正数，总有函数定义域中的x值，使得|f(x)|>M成立，则称函数f(x)为无界函数。

例如，函数f(x)=sinx在它的定义域上有|sinx|≤1成立 所以，正弦函数在整个定义域上为有界函数。而函数f(x)=lnx，因为找不到一个正数M，使|lnx|≤M在(0，+∞)上成立，所以f(x)=㏑x在(0，+∞)上是无界函数。

应该注意的是：

(1)绝对值不等式|f(x)|≤M，等价于不等式-M≤f(x)≤M，即函数f(x)应同时保证：

f(x)≤M，且-M≤f(x).

我们把M称为函数的上界，把-M称为函数的下界。

例如，y=sinx的上界为1，下界为-1.所以，如果函数f(x)是有界的，它就必须是既有上界又有下界。

在平面直角坐标系中，如果函数f(x)是有界函数，则函数的图象夹在平行于x轴的两条直线y=M和y=-M之间。当然，这两条直线未必是函数图象的切线。

(2)如果函数f(x)在某一范围内有f(x)≤M，则称这个函数在这个范围内有上界。例如，函数f(x)=-x²在整个定义域上有上界，且上界M=0。

(3)如果函数f(x)在某一范围内有f(x)≥-M，则称这个函数在这个范围内有下界。例如，函数y=x²-1在整个定义域上有下界，且下界为-M=-1。

(4)函数的有界性既可以在函数的整个定义域上讨论，也可以在定义域的部分子区间上讨论。例如函数y=1/x在整个定义域x≠0上既无上界又无下界，但在(-∞，0)上有上界，在(0，+∞)上有下界，在区间[1，+∞)上则是有界的，这是因为在这个区间上有不等式|1/x|≤1成立。

注 区间的一部分叫做该区间的子区间。

所以，在研究函数的有界性时，一方面要注意函数本身的性质，另一方面要明确研究的范围，只有在整个定义域有界的函数才能一般的称为有界函数。

上期链接：

https://m.toutiao.com/is/ircUvN7c/ - 百科漫谈：名师彻底讲透初等函数(20)利用二次函数的图象解一元二次方程 - 今日头条https://m.toutiao.com/is/ihH465QY/ - 百科漫谈：名师彻底讲透初等函数(21)利用二次函数的图象解一元二次不等式 - 今日头条https://m.toutiao.com/is/iB73HhUu/ - 百科漫谈：名师彻底讲透初等函数(22)一元二次不等式的解的讨论 - 今日头条https://m.toutiao.com/is/iSvegpUC/ - 百科漫谈：名师彻底讲透初等函数(23)有理指数的幂函数y=x³ - 今日头条

https://m.toutiao.com/is/iAosA6S7/ - 百科漫谈：名师彻底讲透初等函数(24)函数的奇偶性 - 今日头条

下期预告：

名师彻底讲透初等函数(26)函数的增减性

3. 增函数和减函数

函数y=x³的图象是从左到右逐渐上升的，我们把具有这种特征的函数，叫做增函数。同样，我们把图象从左到右逐步下降的函数，叫做减函数。例如函数y=-x就是一个减函数。

......