当今科学的某些领域离不开一种强大而复杂的数学工具——张量。尽管它听起来很抽象，但它却是如此重要和有趣。在我们开始探索这个神奇的数学结构之前，让我以一种更口语化的方式给你介绍它。

想象一下，你正在踢足球。每个球员都有自己的位置和角色，他们需要通过传球和移动来配合。现在，把每个球员看作一个向量，他们不仅有空间位置，还有速度和方向。当球员传球时，我们可以使用张量来描述这个过程。张量可以告诉我们球的速度、传球的力量以及球员之间的关系。

那么，张量到底是什么呢？你可以将其视为一个多维数组。就像一个普通的数字代表一个点，一个向量代表一个方向，一个矩阵代表一组数据，一个张量则是一个包含更多信息的数据结构。它可以有任意数量的维度，并且每个维度都可以有任意大小。

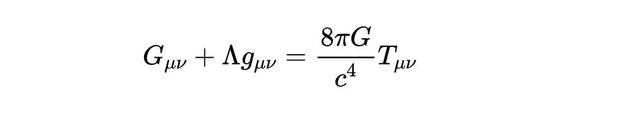
张量的魅力在于它的灵活性和表达能力。无论是描述宇宙大爆炸的起源，还是研究神经网络中的信息传递，张量都可以派上用场。它们能够帮助我们理解复杂系统之间的关系，甚至是在微观和宏观层面进行建模。

让我举一个例子来说明。假设你正在研究一种新型材料的弹性特性。你想知道在不同的应变下，材料会如何响应。这就涉及到张量的运算了。通过测量应变和应力的变化，你可以建立一个描述材料性质的张量模型。

张量还可以帮助我们理解相对论和时空结构。爱因斯坦的广义相对论是描述引力的一种理论。在这个理论中，时空被视为一个四维的张量结构，描述物体如何弯曲并影响其周围的空间。

尽管张量在数学和物理领域扮演着重要角色，但它们也可以在其他领域发挥作用。例如，在计算机科学中，张量被广泛用于图像处理和机器学习中。它们允许我们从复杂的数据中提取有用的信息，并进行高级分析和预测。

正是因为张量的抽象性和灵活性，它们成为了一种无处不在的工具。无论是探索宇宙的奥秘，还是解决实际问题，张量都扮演着关键的角色。所以，下次当你听到张量这个词时，不要被它的复杂性吓到，而是想象一下它背后的丰富内涵和无限可能性。