之前,在铜牛角高考群里有家长提到一种社会现象:
最近几年,很多家长正在打算重新参加高考,以社会考生的名义报名,跟自己的孩子一起“竞争”!
这种神奇操作到底为哪般呢?
据说,目的是通过家长垫底的成绩,来推高自己孩子的高考分数。
不过由于各地考生人数众多,而实际参加考试的家长人数有限,这种操作没有任何实际意义,只会浪费社会资源。
铜牛角也倾向于认为:此种操作不具有可行性,坊间传闻罢了。
但通过详细分析此种行为之所以不可为,可使各位家长对高考赋分,以及高考省位次有更深层次的了解。故寻根查据,以山东省2022年高考一分一段表做依据,推测并证明之。
铜牛角将这一证明题称之为:“家长高考之猜想”。
如果某市或某校的家长比较团结,通过报考物化生史地政中特定的一科,尤其是选科报名人数较少的科目,通过增加报考人数,用家长们的低分,来托高自家孩子的单科分数,那么这么做是否会取得一定竞争优势?
假设大量家长集中参加某一科考试,请问对正常考生分数会有什么样的影响?
铜牛角经过测算,发现结果令人吃惊,居然真的有考生可以增加分数!
那么至少需要多少家长参加考试?经过这么一番操作,有多少考生能获益呢?且听铜牛角娓娓道来。
一、赋分公式

附图1
山东高考赋分制:
山东采用的是3+3模式,语文、数学、英语采用卷面分,政治、历史、地理、物理、化学、生物六科中任选三科采取“赋分制”。山东采用的5等8级赋分制。等级考试科目原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级。
附图2
处于A到E某个等级区间的考生,要按区间进行赋分根据等级赋分公式,考生分数转换需要求一元一次方程, 看上去复杂无比。

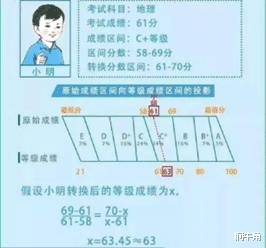
其实大可不必如此麻烦,根据赋分的本质,就是根据原始分,将考生按比例划分出来;先确定属于A到E的哪个等级(例如小明61分属于C+),等级上限按上限分计算(70分),等级下限按下限分计算(61分),处于区间的中间,需要做转换,一个等式即可完成。
小明的原始成绩61分,属于C+等级,比例27%-50%的区间。
那么他的赋分成绩用下述公式换算即可:
X=T1+(Y- Y1)x9/( Y2- Y1)
X=61+(61-58)x9/(69-58) =61+2.45=63.45≈63
请注意此处红色61是考生原始成绩。蓝色61是赋分下限指定的分数。结果中有0.4545的转换后分数,被四舍五入了。
该计算的核心,就是考生原始成绩61减去原始区间下限58,除以原始区间分数跨度(69-58),然后按9分的比例转换赋分,得到2.45分,加上指定的赋分下限分数61,从而得到转换后的单科赋分,四舍五入后约等于63。
根据上面所举的例子,可以了解到,所有考生单科成绩确定后,按照人数比例的赋分区间也就划定了,每名考生根据自己的原始成绩,被划定到特定的区间。然后使用公式强制转换到61至70这个10分的赋分区间中。同一区间中,考生通过公式转换得到赋分,上限70和下限61也可以直接赋分得到。
二、赋分分值对应
一般的关于赋分的分析讲解,到此步就停止了,其实仍有不少问题未曾提及。
铜牛角要提醒大家注意,由于原始分与赋分区间不能正好一一对应,这样就存在两个原始分数对应一个赋分,或者原始分连续但赋分跳分的情况存在。
例如附图2中,小明所处的区间原始分为58—69,赋分后61—70,这样明显是12个分数对应10个赋分。从表中可以看出,由于计算值需要四舍五入,这样60和61两个分数对应63分的赋分,66和67两个分数对应68分的赋分。

附图3
同理附图2中,如果C等级区间原始分为52—57,赋分后51—60,这样明显是6个分数对应10个赋分。从表中可以看出,赋分后分数不连续,有些分数被跳过。

附图4
三、赋分区间人数
由于原始分是0分到100分的可能性,赋分区间却限制在21分到100分,这样就是101个分值对应到80个分值上,这样必然有不能完全对应,存在2个原始分对应1个赋分的情况。
A等级、E等级的人数占比都是3%,这两个区间是人数最少,变化最大的区间。由于赋分是按原始分区间划分,然后强制转换赋分,假如100人考试,前3%里1个最高分100分赋分100分,2个次高分80分赋分91分;后3%里2个次低分20分赋分30分,1个最低分0分赋分21分。最低分0分的看上去好像获利较大。

附图5
这是由于样本人数太少导致的,高考中单科人数至少24万人以上,此种情况就基本不会出现了。
由此看出,分界点的确定,是根据赋分区间人数决定的,那么同一场考试中,大多数考生的成绩密集度,决定了赋分分界点。而分界点确定以后,赋分区间内,每名考生各自对应公式赋分,反而与成绩密集度无关。
实际出题时,由于题目倾向于增加难度和区分度,那么实际得分中,0--10分和91—100分人数较少,人数分布应该绝大多数分布于跨度等于或小于80分的区间,基本上原始分与赋分的对应,也能实现1比1对应。
四、赋分区间分界点调整
原始分区间划分,是按人数划分的,理论人数和实际人数肯定不对应,那么划分依据就是按最接近的原则。
假如E和D区域,因为人数需要调整,那么如果分界点的原始分变动1分,变化趋势如下:
附图6附图7

可以见到原始分分界点下移一分,只能影响到大约10分赋分区间的分数变化,均增加1分。
这个结果和公式计算是一致的。
D和E区间的分界点下移,使得D区Y1减小,E区Y2减小。
根据公式可知:
T1+(Y-Y1)/( Y2-Y1)X9=X
处于分界点的考生,由于分界点向下变动,必然有1分的增加。
D区间,Y1减小后,会使整个分式的数值增大,如果小数点后数值变化达到四舍五入的临界点,那么X的值就会加1。
E区间,Y2减小,也会使整个分式的数值增大,如果小数点后达到四舍五入的临界点,那么X的值就会加1。
整体上看临近分界点的区域,赋分变化增加;由于变化导致的四舍五入越来越小,故远离分界点的区域趋向于赋分不变化。
假设大量家长集中参加某一科考试,请问对正常考生分数会有什么样的影响?
请见本文下篇,且听下回分解。
