他们用尺子测量出来的π和我们并没有区别，就是 3.1415926……

然而他们观测（或者说用光测量的）到的π，则随着空间曲率的不同，在不同的地方有着完全不同的值。

黑洞周围的空间，其实就是一个黎曼空间（内部曲率大，外部曲率小）：

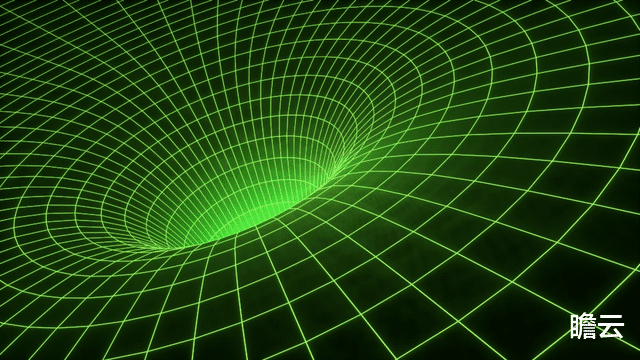
这个黑洞文明用尺子（或者用脚步丈量），无论居住在哪里，它们所画的圆，π都会和我们一样。

不过，作为外部观测者来说，我们看到他们所画的圆应该是这样：

如果在黑洞边缘画圆，圆就会是一个靠近黑洞部分收缩，远离黑洞部分放大的形状。这是因为内部曲率更大，空间更加压缩。外部曲率更小，空间更加膨胀。

那么对于外部观测者看来，它就不会是一个正常的圆，计算出来的π值自然可能和我们不一样（当圆心不在黑洞中心时，甚至半径也在变化，只能求平均半径和π值）。

但如果我们把视野放在足够小的局部，用尺子去测量它的圆弧时，又会发现它是一个标准的圆，π的大小也完全符合数学逻辑。

这是因为，无论人还是尺子都是空间的一部分，大小都是随着空间曲率变化而变化的。在圆靠近黑洞的部分，尺子会变得更短（相对于外部观测者）。而远离黑洞的一部分，则变得更长。

这样，就造成最终用介质测量出来的数据，依旧是一个标准的圆。

因此，对于这个文明，会发现这样的奇怪的现象：

当它们画一个足够小的圆时，会发现整体观测这个圆是很标准的，π值和我们没区别。

当他们用尺子，根据标准的弧度画出一个巨大的圆时，它们观测这个圆的局部时，它总是可以接近完美（局部空间接近平直）。然而，当他们逐渐远离这个圆，同时观测这个圆的整体时，会发现这个圆，变得不规整了。

而且他们还发现，把圆画在不同的位置。在外部观测时，圆的形状都截然不同，而且测出来π也完全不同。

鼠标画的圆不标准，不要介意

虽然为了日常生活计算方便，它们依旧会使用那个尺子测量出来的，固定不变的π 。

然而，为什么不同位置的观测尺度和 π 总是在不断变化呢？

这个现象，会让这个文明在发展出高等数学前极其的困惑。

不过高等数学发展以后，这个世界的黑洞文明黎曼很容易根据观测到的数据，发现了自己所在的世界是一个非平直的空间，于是发展出了黎曼空间。

而这个世界的黑洞文明爱因斯坦，也很容易判断出光速不变原理，提出了相对论。

所以，对于黑洞附近的文明来说，它们所用的π，其实和我们不会有任何的差异。

然而因为观测数据和介质测量数据的差异，这会让他们很快发现相对论效应，极有可能成为这个世界的基本常识。

PS：

当讨论黎曼空间的时候，我们一般会认为黎曼空间的π比平直空间的更小。

但其实，这个结果是站在外部观察者的视角得出来的。

对于生活在这个空间上的人来说，它们的尺度和速度都是随着曲率的不同而变化的。因此，用尺子或脚步丈量的数据结果，和我们这个世界并不会有任何的不同，自然π也一样。