原创 李天王 公子镔 2024-06-04 18:49 福建

甲辰年 己巳月 己亥日

後學 李天王

目錄

天地設位

天圓 1 數

地方 2 數

天有十二次。地有十二辰

次之於辰。上下相值

雜而成文謂之爻

上文天 X

下文干 Y

Y ǖ 不可思議

ye = the

yat = that

葉。業

口上為腒

口下為函

兌為羊

八卦象符號 ☰

八卦數符號 1

八卦文符號 乾

英特爾 4004, 8008

數據壓縮和解壓縮

八卦九宮

易经的象学，首先建立天地的空间结构，这个叫天地设位

天地设位之后，空间结构一般设为两种，天圆结构，地方结构

天圆或地方结构设置好后，我们就划分空间

对于空间的划分单位，在天为次，在地为辰

二十八宿，划分为十二次

二十四气，划分为十二辰

太极既判之后，从天数一，地数二开始，阴阳气数不断变化

接着，日月星辰，从一重天到十二重天，不断跃迁或者降级，从而有辰次的不断变化

我们翻译为西方数学语言，是这样理解的

首先是天圆算法的基本结构图

举例来说

x1 - x12

这就是十二次的一种算法

算法一般分，天圆算法，地方算法

举例计算，天圆算法的表示式

sin²θ + cos²θ = 1

这个 1 数，是指天数 1

这里不是指数字，而是指天一的整个空间范围

明白了天数一，我们开始认识地数二

一是天数的开始

二是地数的开始

阴爻是这样表示的：

象是表达空间概念的，转换如下

圆是径一围三

方是径一围四

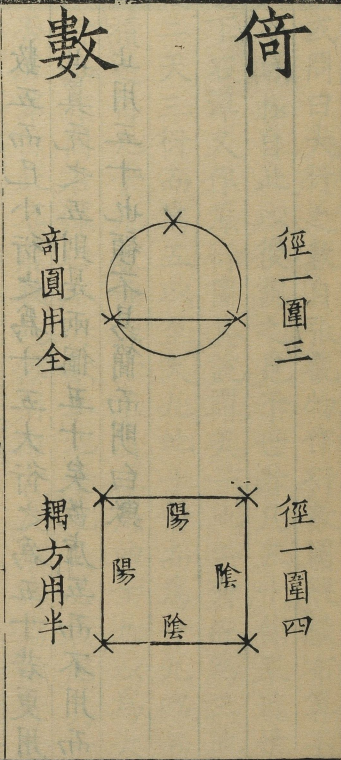
所以这里是一个正方形结构

于是，地方算法的表达式

a² + b² = 1

当我们这样写的时候，表示的是地数二的空间范围

天圆一数，地方二数，他们处在同一个空间范围，所以

天圆算法跟地方算法，构成互相转换的关系

这就是古人说的

天圆为上值，地方为下值，上下值相等

那么，在天地空间的辰次，层次划分好之后，我们就把日月星辰按照时间函数排列

易经的数学计算，就是计算，一个设定空间内，星数的顺序，次序，如何合理安排

简单的说，给定一个有限空间，如何合理安排星数，最大程度利用空间，就是易经数学的任务

那么，我们首先对数量进行分级

古人一般划分为三级计算

在科举中

童生计算万级数

举人计算垓级数

进士计算万垓级数

七八不变，六九究变

文字的上部为六九，下部为七八

杂而成文谓之爻

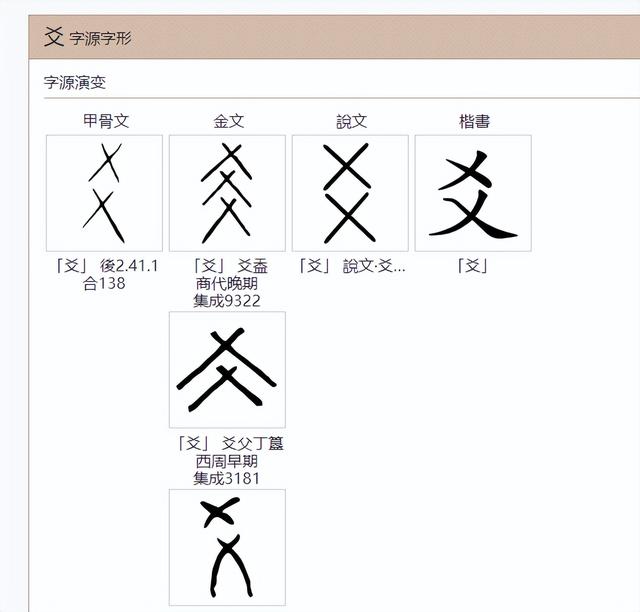
甲骨文，文的写法，可以拆解

所以早期字母 Y，是干的写法，起笔有一个点

字母 Y 是罗马字母表第 23 位

在 Y 出现之前，使用 i, U, V 字母表示，发音为 ǖ

古人认为，天象如下图所示

天象的符号表示方式有

∩ ∪ ∧ ∨ ⌒

所以，在英语词汇中

用 up 表示天，un 表示正反，不可思议等概念

西方数学有一个非常重要的符号表达方式，就是字母以上标下标，字号缩小的形式书写

这是为了弥补字母语言字库天生不足的问题

例如，字母 y，变成上下标形式

具体来说

当然，最关键的，就是西方数学的符号

根据上面的解释，还有符号是

写到这里，我们就知道，x2, xy，是怎么来的，意思是什么

所以，从牛顿时代起两百多年，西方数学是作为拉丁语英语字典的补充而出现的

易经的象学，是设计一个空间结构

易经的数学，则是在这个空间进行点数，数数计算

我们以坤作成物图为例

我们首先给出一个坤的空间

其次，二，是地数的开始，所以坤从二开始作功

翻译为西方数学语言是

注意地数 2 的排列，首先跟坤的空间位置一致

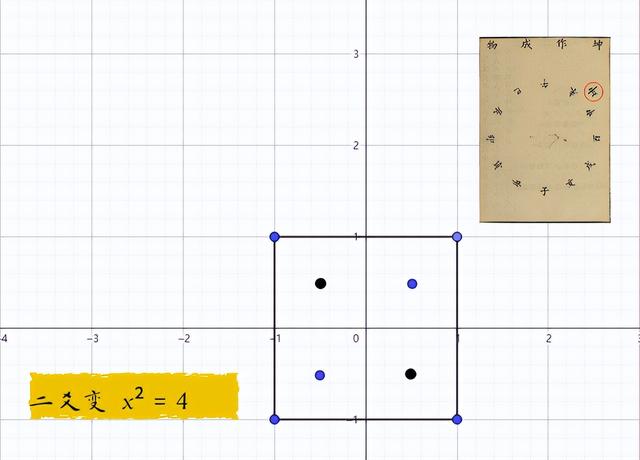
我们可以给八数进行编号

最后我们可以赋予 x 变量属性，变量区间范围，正负属性

注意，葉，業，是兩個字

約克意思是葉家

紐約意思是新葉家

揲，諜，在易經數學中，就是矩陣變換，正負變換

伏羲揲筮求卦之法

函，第一意思是容，函含同字

函又指舌

口的上面为腒

口的下面为函

函的易经写法，兑为羊

易

兌為羊 ☱

說掛

商羊，水吉祥，南方火，所以，羊舌即函

天地相函，坎离相交

就是图中的天数和地数相函，简称，函数

八卦有三种符号表示形式，我们以乾一为例

我们把易经的结构和算法，翻译转换为计算机语言

第一步，是划分处理器，内存等的空间，然后进行地址编号，编码

这在易经中，属于空间结构，方位的问题

所以我们看，伏羲八卦方位之图

三爻计算是三元计算，我们首先进行拆分，降元

我们分割八卦空间结构为 x2, y2

从而将三元降为二元，然后进行空间分割，如图所示

八卦的数字部分，表示空间地址编号，编码

八卦的文字部分，表示存储空间的格式，容量大小，信息内容

比喻的话

八卦数字表示你的小区居住地址单元号

八卦文字表示你的户主信息表示方式

所以我们可以这样翻译

上面是八卦象学的分析过程，接下来，我们进行八卦的数学规律计算

易经象学主要是观察，收集数据

而易经数学的任务，则是数据整理，排列，规律计算

最后，易经文学将理想数据，编译为人类语言

所以我们先进行有序排列的工作

那么，在计算机的设计实现方面，我们需要对八卦的三爻，进行拆分

我们首先将三爻拆分为初爻单独一组，二爻上爻另外一组

一根爻有两种形式，一长线，两短线

初爻就是看最下面的一条线，然后我们按照初爻一长两短，分成两组

计算机处理器，就是严格按照八卦原理设计的

例如，英特尔 4004，1971 年版本

首先拆分的初爻

阳爻正，为输入端，阴爻负，为输出端

数据总线 data bus输入输出 I/O阳爻为正，输入 in 阴爻为负，输出 out

然后我们看二爻上爻组合，分成乾组四数，坤组四数

4004，就是指乾组四数，坤组四数

初爻删除之后，乾组坤组是一样的，只是地址不同，只要做一个地址指针对应即可

如下所示，针脚第一位到第四位，为数据总线出入部分

后续扩展为英特尔 8008, 1973 年版等系列

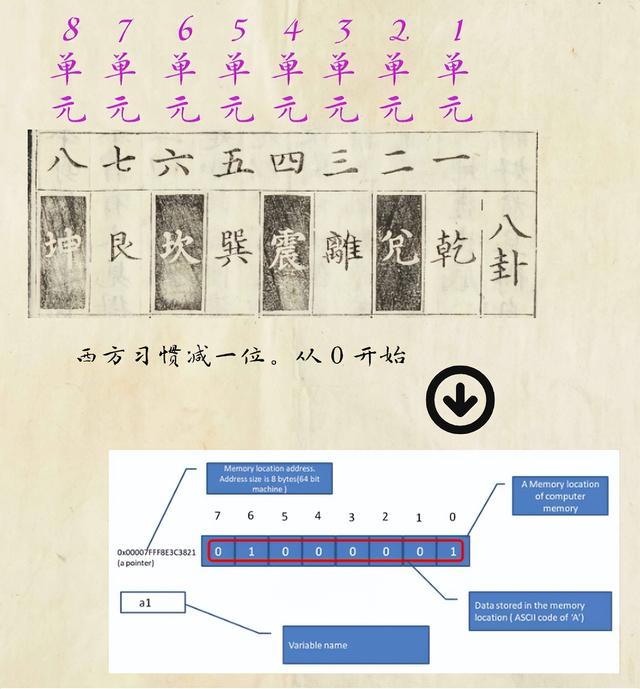
现在，我们将易经设计原理，翻译为西方计算机语言格式

首先是将八卦横排，然后初爻一组，二爻上爻一组

按照西方语言习惯，地数 2，要改为符号 0

这里只是方便大家理解现有的计算机教材

以后我们一定要将计算机的 0 符号表示，修改为地数 2 数，否则就跟易经原理产生矛盾

我们将八卦的完整信息，用计算机设计实现，整个结构如下

在具体的硬件设计方面，则只要照搬易经象图的设计稿

首先是八卦成列，按照

天 4 单元，天 2 单元，天 1 单元

地 4 单元，地 2 单元，地 1 单元

中间大业 1 单元

易经的致用图，就是计算机的硬件设计原理

我们重点看，芯片针脚，然后对比六十四卦致用之图

初爻阴阳，表示正极，负极

然后五卦一组，三组一合

地址 address 缩写为 A

数据总线 data bus 缩写为 D

乾坤八卦，对应数据总线指针针脚

第一针脚到第八针脚，D0-D7

其他针脚分别为地址总线，处理器控制等等

为什么有易经数学呢？易经数学产生的第一个目的，是数据压缩

计算机所有的硬件设计，最终是一个加法器

数学所有的计算，最终是一加一

由于资源和科技条件的限制，古代的书写工具，书写载体，是非常稀有的

所以读书写字，是少数阶级才拥有的

对书写载体空间的有效利用，就成为长期，重大的研究课题

在这种历史情况下，就诞生了易经数学

就是说，数学作为书写工具，用来帮助数据压缩，最大程度利用书写空间

全象拥有最完整的信息，属于全息性质，但是占用资源，空间太大

但是我们排列整齐之后，空间就得到很大的利用

我们可以将空间进一步压缩

我们翻译为西方数学，笛卡尔坐标系，就是这样的

我们把图片旋转一下

所以，当我们看到数学的等号，第一步理解，是数据的压缩和解压缩的互逆过程

我们依旧以多项式因式分解为例

现在我们看多项式因式分解

等号一边是加法项，一边是乘法项

在八卦图上，是这样理解的

加法项就是八卦次序排列

在乘法项中，括号表示空间的分割

八卦方位，就是空间划分，单位为宫

八卦共分割为九个空间，称为九宫

翻译为西方数学语言，可以用笛卡尔坐标系简单表示

中学数学代数，多项式，因式分解，主要目的是计算一万以内的数

符号函数的主要目的，是将数据进行压缩

括号表示空间的划分，我们设一个纵行空间，一个衡行空间

行，读五行的行

纵行衡行，五行相乘，就产生九宫数

将乘法转换为加法，就是数据解压缩

可以看出，目前的现代汉语数学教材，是让学生在走迷宫，猜谜语，这不是好的教学方法

数学不是真理

数学仅仅是工具，永远都是工具