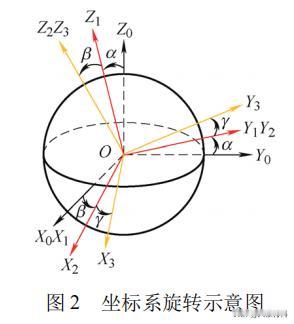
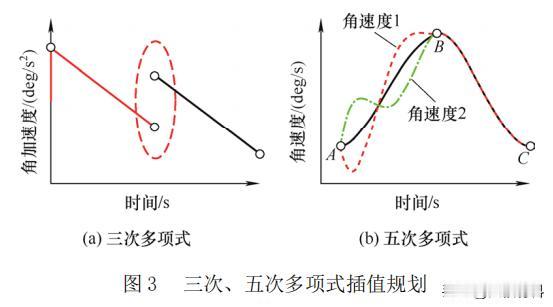
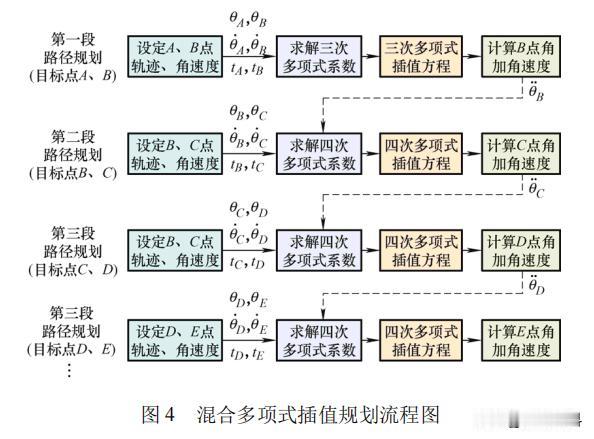
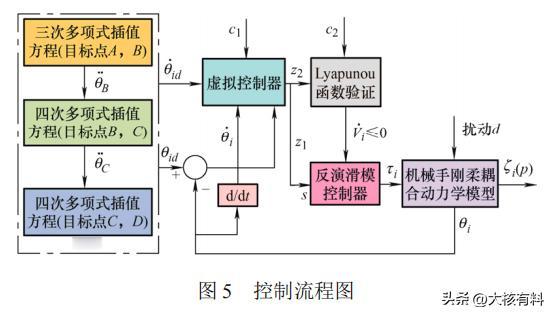
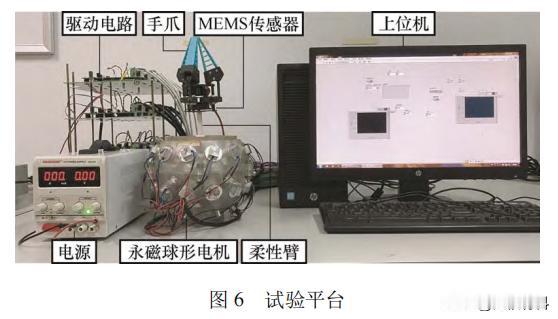
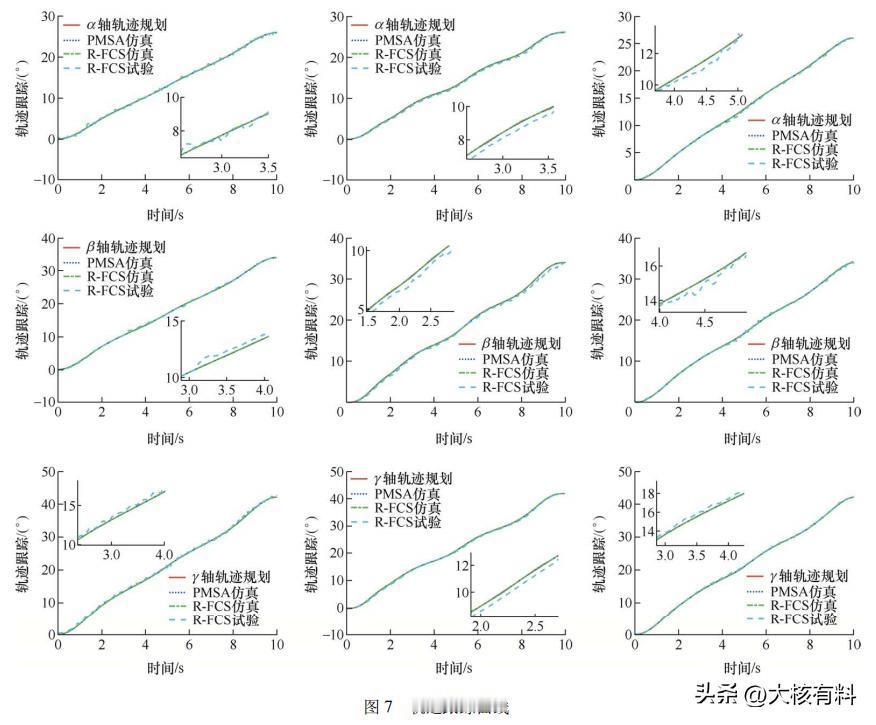
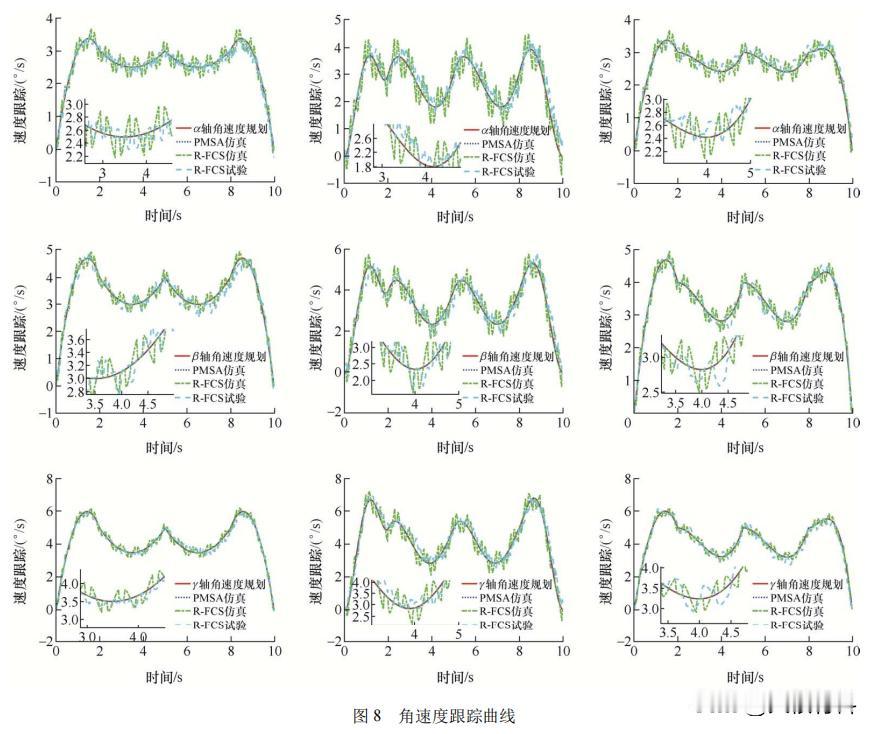
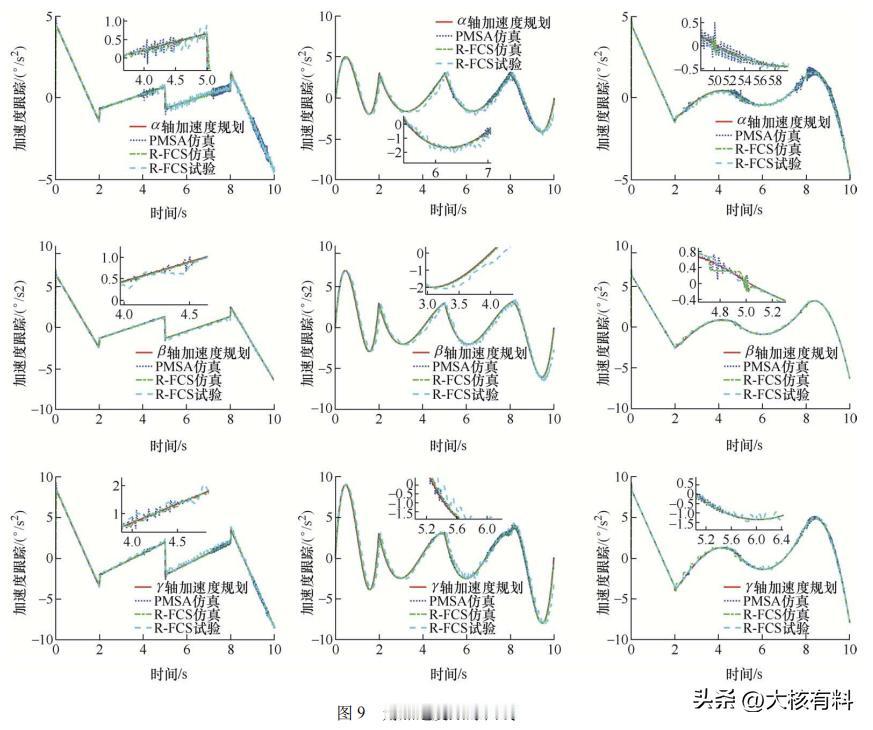
基于混合插值规划的，机械手腕关节用球形电机，能实现高精度轨迹规划？ 现代工业科学技术的日益发达，执行多自由度精密运动的设备在机器人关节、卫星姿态控制等方面获得了应用，球形电机作为一种可以实现多自由度定向运动的新型特种电机，无需额外的机械传动机构，是解决多维运动的重要方案。 2018年，某科研小组开发了一种软体机器人腕关节机构，用于恶劣的深海环境中进行精密操作，为远程控制操作提供方便。 2021年，技术人员将智能手腕机器人应用在外科手术领域，配合操作人员视线跟踪，可大大增强协同操作能力，提高手术安全性。 但随着机器人技术的不断更新换代，传统单机械机器人因其刚性结构导致其运动缺乏一定的平滑性，不适用于一些柔顺环境，同时高精度、自适应性强的机器人，已经成为未来的发展趋势。 本篇文章依据Hamilton原理对柔性臂进行分布式有限维逼近，推导了机械手关节用球形电机刚柔耦合系统的动力学方程，提出一种改进的混合插值规划方法，最后搭建机械手关节用球形电机刚柔耦合系统试验平台，通过仿真和试验证实了所提方法的有效性、准确性。 机械手腕关节用球形电机刚柔耦合系统的三维模型如下图1所示，它由球形电机、柔性臂和手爪组成。 为描述球形转子与定子间的相对运动，分别定义固定的定子坐标系O-X0Y0Z0和随动的转子坐标系O-XiYiZi，如下图2所示，转子的每次运动可以分解为，相对于定子坐标系的三次坐标旋转。 已知刚柔耦合系统工作空间的路径点，通过逆运动学可以得到一系列关节角度，然后由插值算法进行轨迹规划，其中轨迹规划中最常用的方法有三次多项式、五次多项式。 三次多项式插值算法因其原理简单，运算量小，因此广泛应用于离散点之间的插值运动规划。但当处理速度约束的点对点运动时，多段规划连接点处会出现角加速度不连续、出现断点的情况，引起振动和冲击，从而影响机器人的工作性能和使用寿命，如下图3所示。 为了降低轨迹规划给控制系统带来的计算冗余，增加整个刚柔耦合系统的反应时间，我们将三次多项式和四次多项式插值算法相结合，进行速度约束的点到点关节运动规划。 这样使得四次多项式轨迹路径获得较为平滑的角加速度，有效解决了单一多项式插值路径规划方法的不足，其原理和过程如下图4所示。 根据上面所推导过程，为了获得系统较为理想的位姿跟踪曲线，采用反演滑模控制策略，使整个闭环系统满足期望的动静态性能指标，系统控制框图如下图5所示。 为了证实所提轨迹规划算法的有效性，对机械手腕关节用刚柔耦合系统，进行速度约束的点对点指向试验，试验系统如下图6所示。 以运动规划轨迹作为系统的输入，设置三组试验进行验证，三组试验均在反演滑模控制策略下进行。第一组采用三次多项式路径规划方法，第二组采用五次多项式路径规划方法，第三组采用本文提出的“3-4-4-4”混合多项式路径规划方法。 下图7为三个轴向欧拉角的轨迹跟踪试验，3种路径规划方法下角位移曲线都能满足系统三个轴向目标点要求，能够按照给定目标点完成点对点运动规划，且没有太大差别。 相较于单一的多项式插值运动规划，“3-4-4-4”混合多项式路径规划方法在相同控制策略下，试验均方误差值均小于其他两个路径规划方法，因此试验结果验证了所提控制器在外部负载扰动下轨迹跟踪的准确性和鲁棒性。 由下图8可以看出，球形电机刚性输出轴由于不受柔性变形的影响，其偏转角速度较为平滑，而刚柔耦合系统的偏转角速度是沿着给定轨迹曲线发生上下抖动式的变化，试验结果也验证了这一现象。 图9是三种规划方法的角加速度曲线，从图中可以明显看出，球形电机刚性输出轴由于机械振动的原因，导致角加速度会随着运行时间逐渐抖动明显，而机械手刚柔耦合系统角加速度曲线变化较为平滑，抖动较弱。 另外三次多项式插值在规划点处有明显的间断点，会对刚柔耦合系统产生冲击，大大减小电机线圈的使用寿命。而五次多项式插值规划方法虽然在连接点处是连续的，但是可以看出波动较大，不利于刚柔耦合系统的工作性能。 本篇文章提出了一种具有多自由度、柔顺平稳的球形电机刚柔耦合系统，以实现灵活的机械手关节空耦合系统的动力学模型，基于Harmilton法建立了机械手腕关节用球形刚柔“3-4-4-4”混合多项式路径规划，并结合反演滑模控制策略，实现了较为准确的跟踪控制。