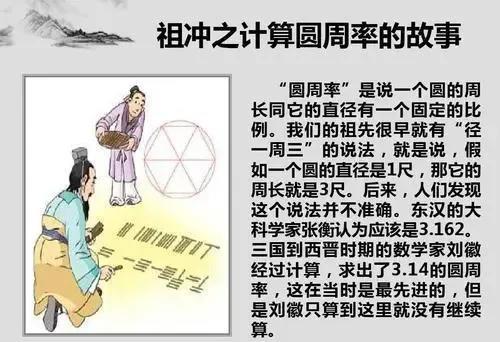
祖冲之（429-500年）将π值精确到小数点后第七位，表明中国当时的古代数学水平已经大大领先世界超过一千年。 问题在于，哪个时候他是怎么计算出来的呢？原来是他将刘辉的“割圆术”推至24576边形。可以想象，这在近两千年前的古代得需要多大的计算量。 核心思想：用内接正多边形逼近圆的周长。多边形边数越多，其周长就越接近圆的周长。 1. 从圆内接正六边形开始（六边形的边长=半径）。 2. 不断倍增边数（12边→24边→48边→96边→……），计算新多边形的周长。 3. 当边数足够多时，多边形周长几乎等于圆周长，从而得到π的近似值。 他计算到了正12288边形（6×212），甚至可能推至正24576边形，远超刘徽的3072边形。而每次倍增边数时，需用勾股定理计算新边长。 所有运算依赖算筹，12288边形的迭代需数十次开方、乘方，极易出错。祖冲之父子（其子祖暅协助）耗费巨大心力完成计算，载于《缀术》（已失传）。 祖冲之通过割圆术的极限逼近和超人的计算毅，将π值精确到小数点后七位，并给出355/113这一精妙分数，展现了古代中国数学的巅峰智慧，祖冲之的π值保持世界纪录近1000年。相比之下，欧洲直到15世纪才由阿尔·卡西算到小数点后14位，而355/113在16世纪才被欧洲知晓。