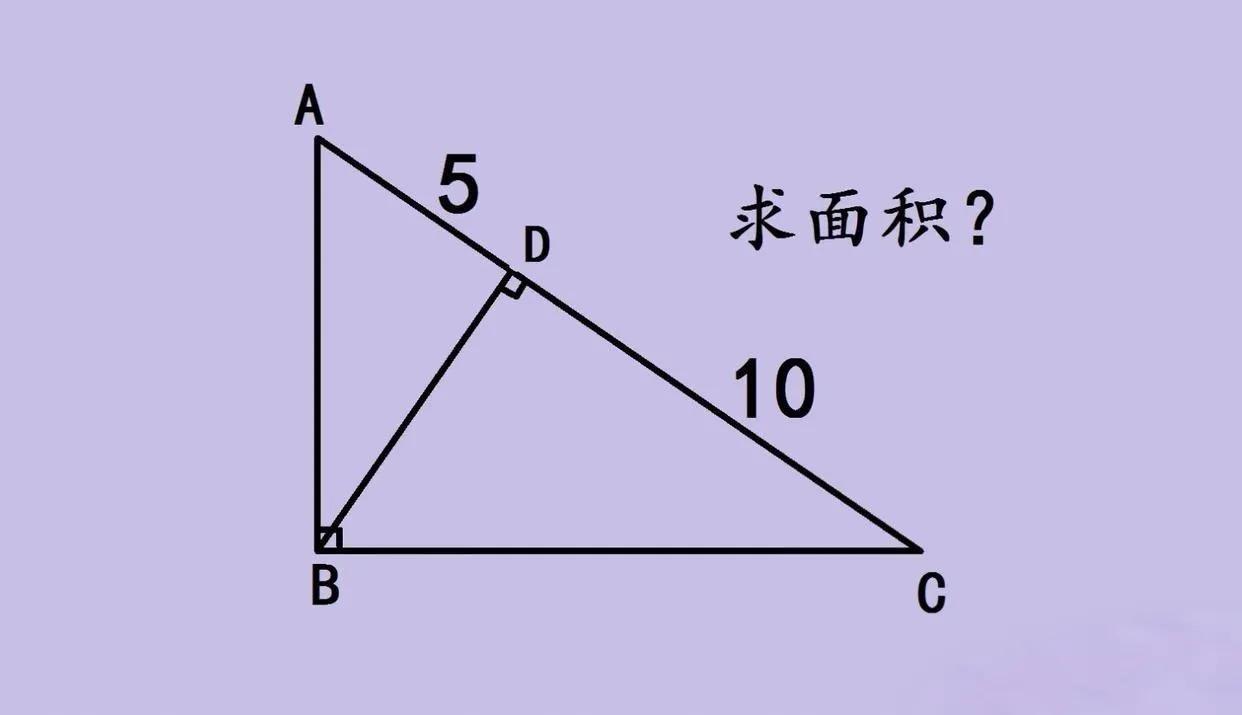
来看这道中考几何求面积题，图形是直角三角形 ABC，∠B 直角，D 在 AC 上，BD⊥AC，AD = 5，DC = 10 。 这题关键是发现隐藏关系，直角三角形里，BD 是斜边上的高，不过还有更妙的！其实可利用 “射影定理” 相关思路（虽初中不直接叫这名，但原理好用 ），或者观察三角形面积的不同表示。 这里有个超巧的点：因为∠ABC 和∠BDC 都是直角，∠C 公共，能推出三角形 ABC 和 BDC 相似，同理和 ABD 也相似 。不过更直接的是，把 AC 当底，BD 当高算面积，但 BD 未知咋办？ 悄悄说，其实这题有个隐藏的等量，直角三角形中，BD 是斜边上的高时，有个特性（可通过面积或相似推导），能发现这题里的面积计算有更简洁的方式，利用已知的 AD 和 DC 长度，结合直角关系，就能快速算出整个大三角形 ABC 的面积，是不是很神奇？中考几何就爱这样，藏着巧妙的几何关系，找到就秒解，你悟到没？