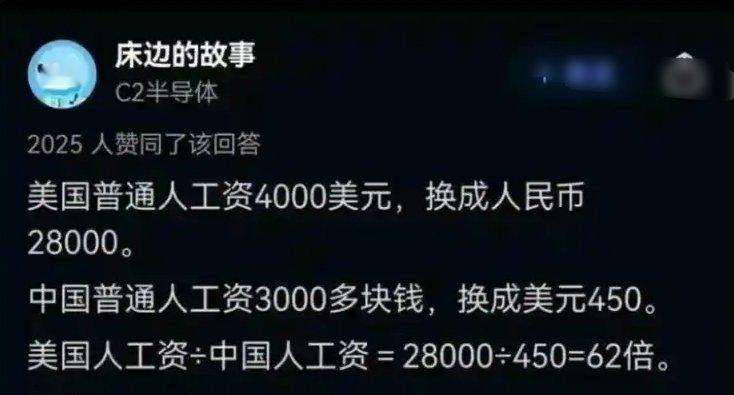
是的,我知道为什么0.999…(无限循环的9)等于1。这是一个常见的数学问题,涉及无限小数的概念和极限思想。下面我会用几种简单的方式来解释,希望能帮助您理解。 我们设 x = 0.999.... (这里省略号表示9无限循环)。 然后,将两边乘以10: 10x = 9.999.... 现在,用第二个方程减去第一个方程 10x - x = 9.999.... - 0.999....= 9 所以, x = 1 。 因此, 0.999....= 1 。 换言之,如果0.999…不等于1,那么它们之间应该存在一个正数差。 但实际上,无论你取多少位9,比如0.999...9(有限个9),它总是略小于1;但当9无限循环时,这个差值会无限趋近于0。 换句话说,1和0.999…之间的差是无穷小,而在实数体系中,无穷小等于0。因此,0.999…和1表示同一个实数。 类似地,1/3 = 0.333…,那么3 × 1/3 = 3 × 0.333… = 0.999…,但3 × 1/3 = 1,所以0.999… = 1。 总之,在数学上,0.999…和1是等价的,只是同一种数的不同表示方式。如果您对细节还有疑问,我很乐意进一步解释!