问题图

如图所示，∠A=60°，BD=31，CD=20，BC=21，求AC.

本文提供两种解法：常规解法和巧解。

常规解法的解题思路：首先考虑在△BCD中，由余弦定理求出cos∠BCD，从∠BCD+∠BCA=180°，求出cos∠BCA，进而求出sin∠BCA，又在△ABC中，由正弦定理求AB，再由∠A=60°用余弦定理求出AC.

解：在△BCD中，由余弦定理，得

∵∠BCD+∠BCA=180°，

∴cos∠BCA=1/7，

由sin²α+cos²α=1可得

在△ABC中，由正弦定理得

在△ABC中，由余弦定理得

BC²=AC²+AB²-2AC·ABcos∠A

(cos60°=sin30°=½)

即21²=AC²+24²-24AC

也就是AC²-24AC+135=0

解之得，AC=15或AC=9，但但AC=9不合题意，舍去.

∴AC=15

巧解

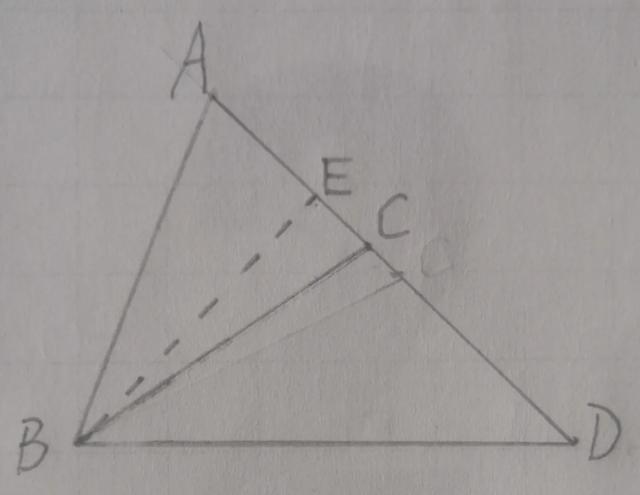
巧解

过B点作BE⊥AD于E，在△BCD中，由余弦定理得

又在Rt△BDE中，

CE=DE-DC=3.

在Rt△ABE中，

∴AC=AE+EC=15

总结：本题所给出的解法是常规思路，即使用正弦定理，余弦定理将已知的边和角构成一定的关系，当然这种关系的建立不一定局限在同一个三角形，时常是两个或两个以上的三角形。

第二种解法(巧解)是利用已知条件中的特殊角，构造含特殊角的直角三角形，从而突出了几何手段。