1989年,一位不知名的编辑在《数学通报》中发表了一篇文章,题目也非常引人入胜——“一维问题的三维呈现”。
虽然现在这篇文章已经不那么出名了,但对于喜欢将空间与平面相结合的数学爱好者来说,这就像是一颗新星出现在天空中。
这篇小文章介绍了一个有趣的问题,并给出了一个独特的证明过程,这引起了不少数学家的关注。
那么,这到底是什么问题呢?
 一维问题引出三维模型。
一维问题引出三维模型。文章的开头提到三个物体,它们被放置在一个边长为n的正六边形盒子中,地面是水平的,每个物体都是物体的一种变体。
它们分别是:
1.
可利颂糖果(以下称为糖果),形状是菱形;
2.
三种不同朝向的糖果摆放着:水平放、左倾放、右倾放。
这个描述乍一看令人感到困惑,但是其中蕴含着一个有趣的一维(组合)数学问题。
我们可以把这个问题抽象为定理:定理1、在一个边长为n的正六边形盒子中摆放可利颂糖果,我们总能以三种不同的方式摆放这些糖果,其中任意两种方式之间没有交集,且这三种方式构成一个分割关系。
具体来说,这三种方式是:
1.
水平摆放,即糖果的边与正六边形盒子的边平行;
2.
左倾摆放,即糖果的尖端朝向正六边形盒子的一角;
3.
右倾摆放,即糖果的另一侧尖端朝向另一个角。

这三种不同的摆放方法,并不是随意选择的,而是显然是完全不同且不重合的。
如果在实际环境中,将这些有不同形状的糖果摆放在六边形盒子里,就会发现格外冲突,甚至完全无法放入。

这就引出了定理2:在一个边长为n的正六边形盒子中摆放可利颂糖果,这些糖果总数为N,水平摆放的糖果总数、左倾摆放的糖果总数和右倾摆放的糖果总数分别记为H、L和R。
定理2:我们始终能够以一种特定的方法摆放这些糖果,使得H=L=R=N/3。

这个定理在直观上是非常令人惊讶和引人思考的,因为我们可以想象,在一个有限的空间和固定数量的糖果上,似乎不太可能出现这样均匀分布的结果。
然而,从定理1来看,这个定理正是要探索这种现象所造成的影响和复杂性。
我们可以进一步探讨这个问题,从多个方面进行分析:
1.
实验验证:尝试在实际环境中进行实验,看看能否得到水平、左倾和右倾摆放三种数量相同的结果,这样可以更好地理解这个定理并加深印象。
2.
数字化建模:利用计算机建模技术,将这些过程数字化呈现,可以更直观地观察和分析,同时也可以进行更多实验。

3.
理论推导:深入探讨这个定理背后的理论基础,分析这种现象产生的原因,可以更好地理解和掌握组合数学领域。
通过这些方法,我们既可以实证检验这一定理,也可以深入理解背后的理论,同时也为进一步研究提供了实践基础。
 “无字证明”是什么?
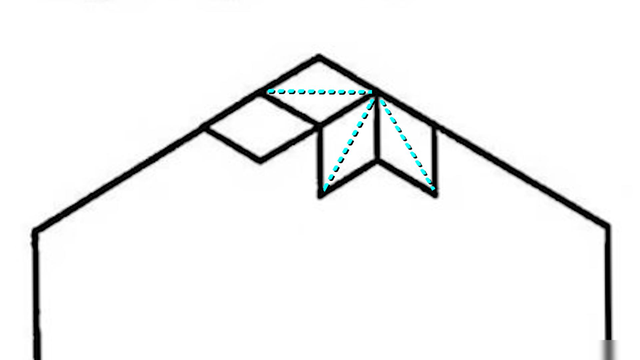
“无字证明”是什么?原文中只是附上了一张图,并没有更多说明。
想起好几年前也看到过一张类似于图中的没写字母证明,只是单纯地把空间想象和数学图形结合在一起展示出解题结果,不得不说,这真是一种非常巧妙而又富有创意的呈现方式!
为了更好地了解这份无字证明,我们可以想象将图片展现在三维空间中,然后将视角从另一方向观看,会移除视图中的部分信息,从而使我们不会看到完整的图像。
但出奇的是,如果我们从不同角度观察,可能会看到完全不同的图案,且每个图案都是完整的,并且以不同方式展示了相同的信息!

那么这些图案是什么呢?
我们可以想象以下数字化建模过程:
首先,我们将正六边形盒子的六个面以平面形式展开,然后每个面上会出现与糖果之间交互相关的信息。
然后,我们从不同角度观察展开后的结果,可以看到:

1.
第一个角度:未见之前,这六个面是不重叠的,但展开后,它们观察到的是平面模型;
2.
第二个角度:在另一个方向观察时,会看到另外一种图案,其中包含其他信息;
3.
第三个角度:继续观察不同方向,又会得到第三种信息模式。
这些不同观察下所得到的信息模式,每一种之间都包含着相同的信息,而这些信息正是说明无字证明所需要表达的重要内容。
因此,无字证明并未留下文字,却以其巧妙和美丽吸引着我们的注意,同时也引发了我们对空间与平面关系的思考。

数学是如此神奇,不仅因为它本身富有逻辑和规律,更因为它能够通过各种方式展现出美丽与奇妙,而这些呈现方式又能够使我们的理解更加深刻和全面。
当然,如果现在不清楚这几个各代表着什么的话,也没有关系,因为无论如何,这都只是个例子,只要贴合实际进行思考,就可以得到通用答案。
 类似的“暴力证明”。
类似的“暴力证明”。这并不是唯一一条能够用这种方式证明的定理,实际上,像勾股定理就有着这样一条非常著名且经典的呈现:
证明勾股定理,只需把两个直角边放上去,再把第三条边表示地圈起来,好吧,勾股定理成立!
当然如果不成立的话,其实最后两个圈也会重叠,不然就不能叫做勾股定理了,哈哈哈。
还有也可以有人提出,把第三条边提前圈起来,然后再推出前两条边来看看能不能装下去,如果能,那么勾股定理成立,如此等等,一些著名结论都有这样的非常有趣的小证明。

这种空间与平面结合的“无字证明”,实际上就是为了展示结论如何能够成立或者不成立,而在过去,这种“无字证明”存在于几个著名结论中,但如今随着信息化时代的发展,它们已经被广泛流传并推广到更多数学领域中。
因此,将空间与平面结合起来,我们不仅能够欣赏这些“无字证明”的美丽,更能够领悟到数学结论成立背后的逻辑,同时激发我们对组合数学领域更深入探索的兴趣。
所以,如果您正在学习或者研究数学,那么一定不要错过这份奇妙而精彩的“无字证明”哦!

