“兰道尔极限和可逆计算芯片”
兰道尔极限

半导体行业一直熟知的定律是摩尔定律:芯片上的晶体管数量大约每两年翻一番。现在,这个速度正在放缓,我们正在遇到一些硬性物理极限。1961年,IBM的Rolf Landauer发现信息是有成本的,每一点信息都要消耗能量。这与物理定律息息相关,特别是热力学定律。这个发现被称为兰道尔极限。在室温下,将一个比特从0翻转到1需要消耗的能量很小,只有2.9x10^-21焦耳。这个数字非常小,通常我们不会在意。
现有计算机芯片,能量都已热浪的形式浪费了

但是当你在计算数十亿或数万亿位(例如最新的 NVIDIA GPU)时,就会消耗大量能量,得到的信息是输出,即操作的结果。在现代计算机芯片中,几乎100%的能量都以热量的形式消散了,因此本质上是浪费了。如果我们可以将这些能量存储在系统中,并回收利用以用于未来的计算,就能大量减少发热问题,并打破兰道尔极限。
半导体行业在逼近兰道尔极限
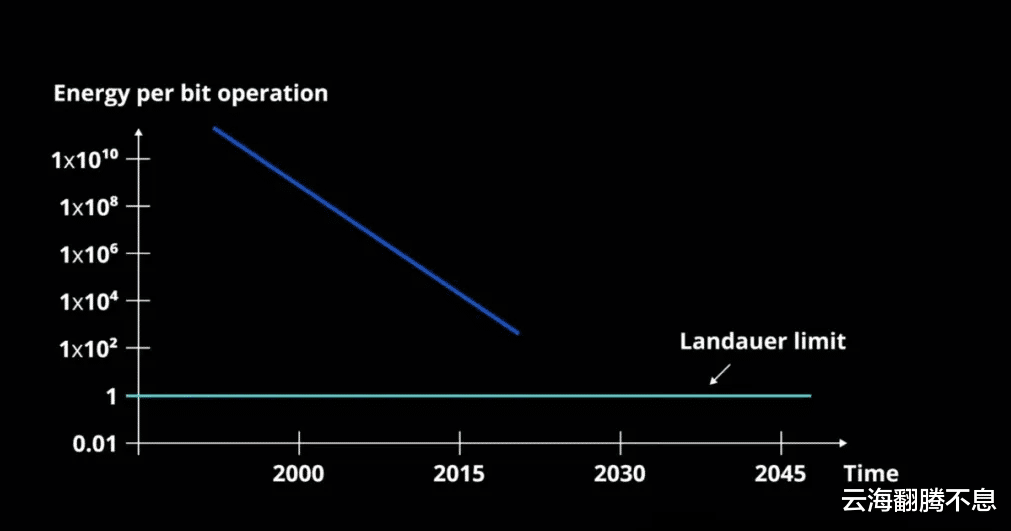
在兰道尔时代,这既不可能也不实用。在过去的60年里,晶体管越来越小、工作电压越来越低、需要充电的电容器越来越小,所以每个操作上每位所消耗的能量越来越少。但随着制程精度越来越高,尽管兰道尔极限非常小,但我们已经非常接近它了,现在我们离它只有几个数量级的差距。尤其是对于CMOS,已经接近兰道尔极限。
费曼对兰道尔极限的质疑

有趣的是,兰道尔本人发现,通过可逆性可以为能耗设定更低的限值。理查德·费曼对这个问题进行了深入探讨,质疑是否有可能超越兰道尔极限。他得出的结论是,如果我们在计算过程中不丢失信息位,即不擦除数据,那么计算所需的能量理论上没有最小值。
现代计算机都使用不可逆逻辑

但现在计算机芯片的构建方式是,当信息不再需要时,我们会擦除它。所有现代计算机都使用不可逆逻辑。以一个简单的逻辑或门为例,得到计算记过以后,输入信息会被擦除,不会保存。但有几种组合能够导致输出为零,我们知道结果的时候,并不知道输入是什么。
可逆计算机能大幅减少能量耗散

兰道尔证明了能量的损失是由于信息的破坏,而不是操作本身的执行。所以如果我们能够建造一台可逆计算机,理论上我们就可以完全不使用能量进行计算。当使用可逆计算时,可以真正将热量的产生与信息的处理分离开来。虽然很难将其转化为我们可以构建逻辑的术语,但当弄清楚了这一点,就可以显著减少信息计算产生的能量耗散。
Vaire 今年将推出首台可逆计算原型机

Vaire是一家初创公司,正在打造第一台商用可逆计算机。这种计算机芯片实现了我们刚刚讨论过的可逆逻辑。他们采用了标准逻辑门,并对其进行了调整,使其以可逆的方式工作。可逆计算需要向前和向后两个步骤,通过向前计算保存输出,然后反向计算生成所有中间和临时数据。芯片消耗的能量没有以热量的形式耗散,而是储存在晶体管中,他们就能够在解算步骤中恢复它。他们已经接近这个目标,第一台原型机将在今年问世。
可逆计算逻辑的原理

为了实现可逆计算,Vaire在可逆逻辑电路中嵌入谐振振荡器。目前它是一个由电感器和电容器组成的 LC 振荡器,电容器是逻辑的电容。当能量在逻辑电路和谐振器之间来回切换时,只有一小部分被耗散,大部分能量可以恢复和再利用。在可逆计算机芯片有一个谐振器,能量在电感器和电容器之间来回反弹,像一个摆动的钟摆。向上摆动时,执行计算步骤,能量流向逻辑电路,为电容器充电。向下摆动时,执行反计算步骤,能量返回到谐振器。
有可能突破兰道尔极限

当然,在现实中,由于寄生效应、谐振器质量、器件特性等原因,总会有一些能量损失,但能量损失要远小于现有计算芯片。采用这种方法,理论上他们可以实现比传统芯片高出三个数量级的能效提升,消除散热问题,并有可能突破兰道尔极限。Vaire仍面临诸多的挑战,既包括制造问题,也包括设计新硬件匹配的软件堆栈。但如果我们能够制造出可逆计算机,就可以解决半导体当前最大的问题,即散热问题。然后我们就可以真正垂直堆叠更多的芯片,构建真正的3D芯片,这将开启计算领域的全新时代。

















