今天一个学生问了我一道题,其实是一道非常常规的反比例函数求k的值,他说看了这道题的参考答案,太复杂,问我有没有更简单的方法。

反比例函数求k值。
这道题真的非常经典,命题方式也是传统型的,考的是纯数学素养,但其实这道题非常考学生的思维能力,找准方法相当于秒杀,非常的快捷。而我觉得这正是数学的魅力,传统的命题方式里面其实大有玄机,这样题目真的有很多种解法,我上课的时候就喜欢学生用不同解法来解同一道题,当思维的闸门一打开的时候,课堂也就充满了活力。
这是这道题的参考答案,它是一种非常常规的思路,设点的坐标,K等于坐标的乘积,思路并不复杂,但解题过程真的太复杂了,居然还出现了二次项。

参考答案
其实这道题,简单与复杂的分界点,就在于设坐标的技巧。这道题设坐标的过程当中,根本就不用一次函数的表达式,也就是根本不用a和b两个字母。

解题方法参考。
大家看一下我上面的参考答案,为了大家看的比较清楚,我写得比较多。其实对一道填空题而言,这道题30秒钟就足够了。设B点的坐标(m,n),根据反比例函数图像上所有点的横纵坐标乘积相等,加上中位线定理,就很容易知道A点坐标是(1/2m,2n)。同时很容易知道三角形OAB的面积等于直角梯形ANMB面积,所以用直角梯形面积公式,就直接算出mn的值,也就是k的值。
这就是数学,不仅仅是完成了一道题,还要去思考有没有最优解决方案,其实这道题还有其它方法,大家可以去思考一下,真的是非常好的一道题。
我们再来看下面这道题,参考答案也异常复杂,甚至出现了一元二次方程,这显然不是最优解决方案。

例2
这道题不要设点的坐标,很明显走面积这条路,求出三角形AOC也就是三角形BOC的面积,而求面积的方法 ,用到的不过是高相等的时候底边之比为面积之比。相似三角形面积比等于相似比的平方。大概也就30秒钟的时间。大家可以看下面我的参考答案。
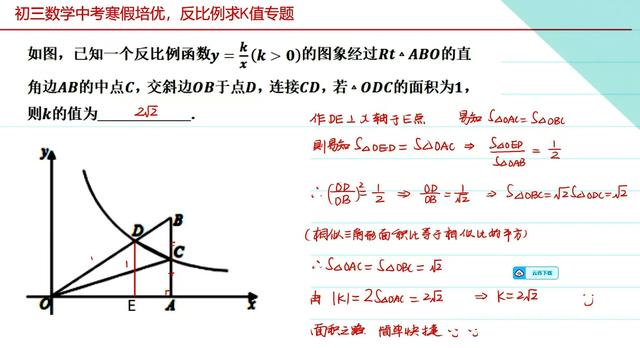
例二,参考答案。
数学要培养数学思维能力和解决方法的能力,一题多解就是一种很好的方式。下面给大家推荐两道题,给了参考答案,你还能想出更简单的方法吗?

练习1

练习2
关注我,推荐数学好题,好方法,好思想。
