全文约1500 字;
阅读时间:约4分钟;
听完时间:约8分钟;

接着昨天,我们通过主计划的工单数量来计算分解比例,然后使用VSTACK函数堆叠重复的数据项,接着利用OFFSET函数获取子件的未领用量需求。为了确保数据的有效性,我们会使用DROP函数去除无效的空行。在整个过程中,SORT函数帮助我们对数据进行多条件排序。通过这些步骤,我们最终实现了用料分析中子件的需求分拆。
 区域转单列
区域转单列通过使用 SORT 函数获得一个子件用料分析的分解数据。因为这个数据是一个区域,为了确保后续对子件库存的引用能继续使用动态数组公式自动扩展,这里采用 INDEX 函数将区域转换为单列公式。输入公式后,向右填充:
=INDEX(TAKE(SORT($AJ$3:$AO$30000,{3,5}),ROWS(AJ3#)),,COLUMN(A1))
公式解释:
SORT($AJ$3:$AO$30000, {3, 5}):首先对 $AJ$3:$AO$30000 区域内的数据按照第 3 列和第 5 列进行排序。
TAKE(…, ROWS(AJ3#)):从排序后的结果中取出与 AJ3# 动态数组同样数量的行。
INDEX(…, , COLUMN(A1)):从上述取出的数据中选取对应于 A1 列号的列作为输出结果。随着公式的横向填充,COLUMN(A1) 会相应地增加,从而选择不同的列。
效果如下图所示:
 累计未领数
累计未领数接下来需要计算子件的累计未领用量,这一步骤是为了后续与库存数据进行运算做准备。此时,工单已经按照用料分析中的子件进行了分拆,例如 WK-01 的子件 A1,在 8 月 20 日到 8 月 23 日的需求分别为 300、300、300,因此累计需求分别为:300、600、900。
录入以下公式来自动计算累计需求:
=SCAN(0,AS3#,LAMBDA(X,Y,LET(A,OFFSET(Y,,3),IF(Y=OFFSET(Y,-1,),X+A,A))))
公式解释:
初始值:0
数组:AS3#,这里代表子件标识符,如 A1/A1/A1 等;也就是后续的 Y 值。
OFFSET(Y, , 3):Y 值向右偏移 3 列,对应的是子件的未领数量,例如 300、300、300 等。
IF(...):如果 Y 值与其前一行相同(即不是新的子件),则返回 X 加上 A(即未领数量累加),否则直接返回 A。这样可以实现未领数量的累加,形成累计需求的序列。
 引用现存量
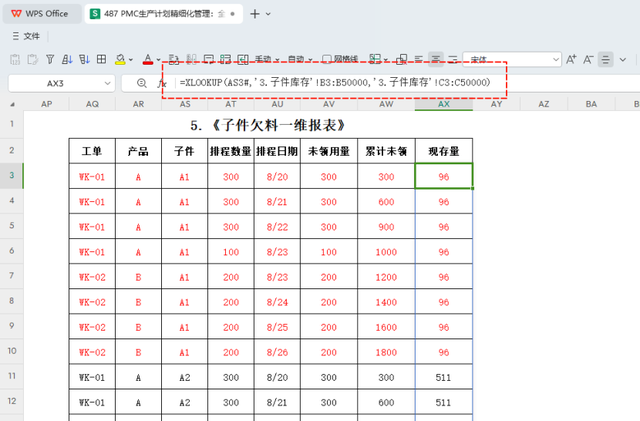
引用现存量累计未领数计算出来后,就需要把子件的现存量引用过来了,在边上新建一列,并命名为“现存量”,这里的现存量确保没有重复项的情况下,可以录入以下公式:
=XLOOKUP(AS3#,'3.子件库存'!B3:B50000,'3.子件库存'!C3:C50000)
公式解释:
此公式用于查找 AS3# 中的每个子件在其对应的库存列 '3.子件库存'!B3:B50000 中,并返回该子件在 '3.子件库存'!C3:C50000 列中的库存量。
如果有重复项,也就是一个子件在多个库位都有库存的情况下,需要更改公式为SUMIFS
=SUMIFS('3.子件库存'!C3:C50000,'3.子件库存'!B3:B50000,AS3#)
公式解释:
此公式用于计算 '3.子件库存'!C3:C50000 列中所有与 AS3# 相匹配的子件库存值之和。其中 '3.子件库存'!B3:B50000 列用于指定查找条件。
 今日知识点
今日知识点区域转单列
核心函数:
SORT, TAKE, INDEX
公式:
=INDEX(TAKE(SORT($AJ$3:$AO$30000, {3, 5}), ROWS(AJ3#)), , COLUMN(A1))
简单介绍:
SORT 函数用于按照指定列对数据进行排序。
TAKE 函数用于从排序后的数据中提取指定数量的行。
INDEX 函数用于从提取的数据中选取特定列的内容,形成单列输出。
累计未领数
核心函数:
SCAN, OFFSET, LAMBDA
公式:
=SCAN(0, AS3#, LAMBDA(X, Y, LET(A, OFFSET(Y, , 3), IF(Y = OFFSET(Y, -1, ), X + A, A))))
简单介绍:
SCAN 函数用于累积计算数组中的值。
OFFSET 函数用于获取单元格相对于起始位置的偏移值。
LAMBDA 函数定义了一个匿名函数,用于迭代数组中的每个元素。
引用现存量
核心函数:
XLOOKUP, SUMIFS
无重复项公式:
=XLOOKUP(AS3#, '3.子件库存'!B3:B50000, '3.子件库存'!C3:C50000)
有重复项公式:
=SUMIFS('3.子件库存'!C3:C50000, '3.子件库存'!B3:B50000, AS3#)
简单介绍:
XLOOKUP 函数用于在一个范围内查找并返回匹配项的值。
SUMIFS 函数用于基于一个或多个条件求和。

