在高维空间中,距离度量逐渐失效的原因主要归因于“维度诅咒”(Curse of Dimensionality)。具体来说,随着数据维度的增加,样本之间的距离趋于相等,这使得传统的距离度量(如欧氏距离、曼哈顿距离等)失去了区分样本的能力,从而导致距离度量失效。
在低维空间中,距离度量能够很好地反映数据点之间的相似性。然而,在高维空间中,由于维度的增加,数据点之间的距离变得非常接近,甚至趋于一致。这意味着即使两个样本在某些特征上存在显著差异,其整体距离也可能非常接近,从而无法有效区分这些样本。这种现象被称为“距离集中”,即所有样本之间的距离趋于相等。
高维空间下距离度量失效的主要原因是维度诅咒导致的距离集中现象,以及计算复杂度和存储需求的急剧增加。这使得传统的基于距离的算法(如KNN、聚类算法)在高维数据上的表现变得不可靠。
高维空间中距离度量失效的数学原理主要涉及以下几个方面:
维度灾难:随着维度的增加,数据点之间的距离变得越来越相似或无法区分。在高维空间中,数据点之间的距离变得非常稀疏,大多数数据点之间的距离相差不大,导致距离度量的有效性下降。例如,在三维空间中,两个点之间的欧氏距离可以很好地表示它们之间的差异,但在高维空间中,两个点之间的欧氏距离可能非常接近,无法准确地反映它们之间的相似度。
数据稀疏性:在高维空间中,数据变得非常稀疏,即使在大数据集上也是如此。这使得计算出的距离值不准确,因为它们不能反映真实的数据分布。例如,高维超球体的绝大部分体积都在球表面的一层薄壳中,这意味着大多数点位于球体表面的很薄的薄壳里,半径为0.999的球体内点的数量随着维数变大趋近于零。
计算复杂度增加:随着维度的增加,计算复杂度呈指数级增长,导致计算变得困难。
非线性关系:欧氏距离只考虑了各个维度之间的线性关系,而忽略了它们之间的非线性关系。但在高维空间中,数据之间的非线性关系可能更加重要。
投影效应:在高维空间中,数据投影到低维空间时可能会失去很多信息,导致距离计算不准确。
几何理论差异:高维向量空间的几何理论与低维是完全不同的。例如,无穷维空间中的球非紧,说明了维度过高会导致度量失效。
大数定理:在高维数据中,大数定理可以帮助我们理解独立随机变量的和如何收敛到其期望的和,即收敛到一个常数。这意味着数据点之间的距离会趋于一致。
高维空间中距离度量失效的数学原理主要涉及维度灾难、数据稀疏性、计算复杂度增加、非线性关系、投影效应、几何理论差异以及大数定理等因素。
如何有效降低高维数据的计算复杂度和存储需求?有效降低高维数据的计算复杂度和存储需求的方法主要包括以下几种:
降维技术:
主成分分析(PCA) :通过选择数据中最具方差的主成分,去除噪声并保留最有用的信息,从而显著减少数据的存储和计算成本。
线性判别分析(LDA) :通过最大化类内散度和类间散度的比值来实现数据的降维,适用于多类数据的处理。
奇异值分解(SVD) :通过将高维矩阵分解为两个或多个低维矩阵的乘积,减少数据的维度,同时降低计算复杂度和存储需求。
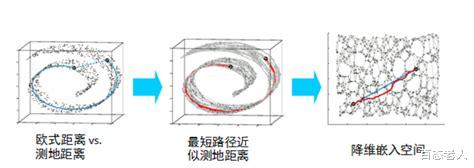
局部线性嵌入(LLE) 和Isomap:这些基于流形学习的降维算法通过最小化重构误差或利用KNN算法来确定相邻点,从而实现数据的降维。
数据压缩技术:
损失表示空间:通过压缩或丢弃部分信息来降低数据维度或复杂度,例如在图像压缩中使用DCT或小波变换将图像转换为低维度表示,丢弃高频部分实现有损压缩。
TF-IDF和Word2Vec:在自然语言处理中,通过将词向量降到200维或更低,可以大大提高计算效率。
分布式存储和计算技术:
通过将数据存储和计算任务分配到多个节点上,提高数据存储和传输的效率,从而降低单个节点的计算和存储压力。
深度学习框架:
深度自编码器网络(Deep Autoencoder Networks) :通过构建全连接神经网络来学习数据的低维表示,从而降低计算复杂度和存储需求。
矩估计:
矩估计是一种将高维数据映射到低维空间的方法,通过保留核心特征,降低计算复杂度和存储需求。
主成分分析(PCA)和线性判别分析(LDA)在高维空间降维中的具体应用和效果如何?主成分分析(PCA)和线性判别分析(LDA)是两种常用的降维技术,它们在高维空间中的应用和效果各有特点。
主成分分析(PCA)原理与实现:PCA是一种无监督的降维方法,其目标是通过寻找数据中的主成分(即方差最大的方向)来降低数据的维度。具体步骤包括:
数据预处理:对原始数据进行标准化处理,使得每个特征的均值为0,方差为1。
计算协方差矩阵:通过计算数据的协方差矩阵来评估特征之间的相关性。
求解特征值和特征向量:通过特征值分解找到协方差矩阵的特征值和特征向量。
选择主成分:选择前k个最大的特征值对应的特征向量作为主成分。
数据重构:将数据投影到新的低维空间中。
应用与效果:PCA广泛应用于数据可视化、预处理、建模和压缩等领域。它能够有效地减少数据的计算复杂度,避免过拟合,并提高模型的泛化能力。例如,在图像处理中,PCA可以用于降噪和特征提取。
线性判别分析(LDA)原理与实现:LDA是一种有监督的降维方法,其目标是将高维数据投影到低维空间,同时最大化类间距离和最小化类内距离。具体步骤包括:
数据预处理:对原始数据进行标准化处理。
计算类内均值向量和类间均值向量。
构造类间散布矩阵和类内散布矩阵。
求解特征值和特征向量:通过求解类间散布矩阵和类内散布矩阵的比值,找到最优的投影方向。
数据重构:将数据投影到新的低维空间中。
应用与效果:LDA特别适用于分类问题,能够有效地保留类间的区分信息,提高分类效果。例如,在人脸识别中,LDA可以用于提取最具区分性的特征,从而提高识别率。
总结PCA和LDA在高维空间降维中各有优势:
PCA:适用于无监督学习场景,能够有效减少数据的计算复杂度和避免过拟合,广泛应用于数据预处理和特征提取。
LDA:适用于有监督学习场景,能够最大化类间距离和最小化类内距离,特别适合分类问题。
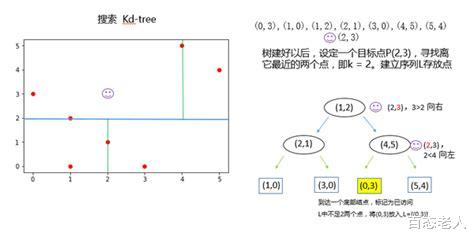
近似最近邻搜索算法(如KD树、球树、局部敏感哈希LSH)在处理高维数据时的效率和准确性比较。在处理高维数据时,近似最近邻搜索算法(如KD树、球树、局部敏感哈希LSH)的效率和准确性各有优缺点。
KD树:
效率:KD树是一种平衡二叉树,通过递归地将k维空间划分为子区域来查找最近邻。在低维空间中,KD树的效率较高,但在高维空间中,其性能会显著下降。这是因为随着维度的增加,数据点的分布变得越来越稀疏,导致搜索路径变长,查询时间复杂度增加。
准确性:KD树在低维空间中可以提供较高的准确性,但在高维空间中,由于“维数灾难”的问题,其准确性会降低。
球树:
效率:球树通过用球体代替超平面来划分空间,适用于处理高维数据。球树的构建时间复杂度较高,但查询效率相对较高,尤其是在高维空间中。
准确性:球树在高维空间中的准确性较高,但仍然存在一定的误差,尤其是在数据分布不均匀的情况下。
局部敏感哈希(LSH):
效率:LSH通过将相似的数据点映射到相同的哈希桶中,显著减少了需要检查的点的数量,从而提高了查询效率。LSH特别适用于高维空间中的近似最近邻搜索。
准确性:LSH的准确性可能较低,因为它依赖于哈希函数的设计。如果哈希函数设计不当,可能会导致相似数据点被映射到不同的桶中,从而降低查询结果的准确性。
总结来说,KD树和球树在高维空间中虽然能够提供一定的查询效率,但其准确性和效率都会随着维度的增加而下降。而局部敏感哈希(LSH)则在高维空间中表现出色,尤其是在需要快速查询的情况下,但其准确性可能会受到哈希函数设计的影响。
自适应距离度量方法在高维空间中的实现方式及其对算法性能的影响。自适应距离度量方法在高维空间中的实现方式及其对算法性能的影响可以从多个角度进行分析。以下是基于我搜索到的资料的详细回答:
实现方式自适应度量学习:自适应度量学习(Distance Metric Learning)是一种在机器学习中用于高维数据降维和相似性分析的技术。其目标是在样本上学习一个距离度量函数,以使相似数据的距离尽可能接近,不相似的数据距离尽可能疏远。通过优化问题来学习距离度量矩阵,确保其满足非负性、对称性、次可加性和不可分与同一性等公理。
相对距离自适应谱聚类(RDASC):RDASC算法基于UMAP降维技术,利用相对距离放大数据点间的差异,并结合基于相对和绝对距离的高斯核函数公式,自适应地确定尺度参数σ,以提高聚类效果。
判别自适应最近邻(DANN):DANN算法通过构造查询点的邻域,并根据邻域内类别的分布来调整邻域形状,以适应类别概率变化的方向。具体而言,DANN使用合并的类别内协方差矩阵和类别间协方差矩阵来定义查询点的度量,然后沿着类间协方差矩阵的零特征值方向拉伸邻域。
耦合自适应距离:在高维遥测数据的异常检测中,提出了一种基于耦合自适应的改进距离定义,并针对归纳监视系统(IMS)算法进行了改进。该方法利用历史数据的分布特征,在进行聚类的同时,对于参数耦合性进行动态挖掘,并将挖掘到的知识高效地投入到异常检测任务中。
对算法性能的影响提高分类准确性:在高维空间中,某些维度可能包含噪声或无关特征,这些特征可能对距离计算产生较大影响,导致距离度量对噪声敏感,降低分类准确性。通过选择更适合高维数据的度量方法,如马氏距离、余弦相似度等,可以提高分类的准确性。
提升聚类效果:RDASC算法在UCI真实数据集上的ACC、ARI、NMI指标分别比传统谱聚类算法提升4.38%、7.37%、4.25%,证明了其在高维数据聚类任务中的优越性。
降低误差率:DANN算法通过自适应度量,显著降低了误差率。在十维空间中的两类别数据生成的例子中,DANN算法与标准最近邻算法和LVQ算法相比,显著降低了误差率。
提高检测效率与准确率:基于耦合自适应距离的高维异常检测算法在与多种传统基于IMS的异常检测方法的对比实验中,检测效率与准确率分别提升了41.83%和69.03%,验证了运用该距离定义的检测方法在效率与精确率上的优越性。
结论自适应距离度量方法在高维空间中的实现方式主要包括自适应度量学习、相对距离自适应谱聚类、判别自适应最近邻和耦合自适应距离等技术。
