【题目呈现】甲乙两人同时从A地出发,步行15千米到B地,甲比乙每小时多走1千米,结果比乙早到半小时,两人每小时各走多少千米?
(解题思路)本题的关键语句是“同时出发”和“结果比乙早到半小时”,应当利用时间相等列方程。
【解】设乙每小时走x千米,则甲每小时走(x+1)千米。
根据题意列方程得

这是一个分式方程。在解题之前,我们进行相关的知识概括。
知识概括在初中阶段,我们学习过分式方程的知识。分母中含有未知数的方程叫做分式方程。
解分式方程的一般步骤:
(1)用一个适当的含未知数的整式(通常取各分式的最简公分母)乘方程的两边,使它变形为一个整式方程。
(2)解所得的整式方程。
(3)把所求得的根进行检验。如果适合的,就是原方程的根;如果使原方程失去意义(即某些分母等于0)就是增根,应该去掉 。
举个简单的例子。
一项工程甲乙两队合作能够8天完成,若乙队单独做能够12天完成,求甲队单独做多少天能够完成?
解 据题意可列方程

这是一个分式方程,各分式的最简公分母为24x,用它乘方程的两边,得
24+2x=3x
解之得 x=24
把x=24代入原方程
左边=1/24+1/12=⅛=右边
∴x=24是原方程的根。
用分式方程解应用题现在我们来解本文开头提出的行程问题。
各分式的最简公分母是2x(x+1),用它来乘方程的两边,得
2x×15=(2x+2)×15-x(x+1)
即
30x=30x+30-x(x+1)
30x=30x+30-x²-x
30x=29x+30-x²
x²+x=30
我们用配方法来解这个二次方程。
x²+x+(½)²=30+(½)²
x²+x+¼=121/4
(x+½)²=121/4
两边开平方得
x+½=±11/2
∴x₁=11/2-½=5,x₂=-11/2-½=-6.因x₂=-6不合题意,舍去。
当x=5时,x+1=6.
答:乙每小时走5千米,甲每小时走6千米。
【常见错误】根据所设未知数列出方程如下:

造成错误的原因是未弄清“早到半小时”的含义。“甲比乙早到半小时”就是“走完这段路甲比乙要少用半小时”,也就是“乙走完这段路程所用的时间减去半小时才能和甲走完这段路程所用的时间相等”。
题目做完以后【回顾和总结】列方程解应用题的首要问题是设未知数。一般有两种设法:直接法和间接法。不论哪种设法,关键是要能更好地沟通已知和未知之间的联系,即便于准确地找出等量关系。
例如,本题变换一些条件或结论后,思路就有变化。
(1)将条件中“甲比乙每小时多走1千米”变换成:
①甲速度是乙速度的两倍多0.5千米;
②开始行走5千米两人速度一样,后来甲有事需加快速度为原来的1.5倍;
③甲乙两人行相同路程所用的时间比为1:2.
根据所设,可列出相应的方程:
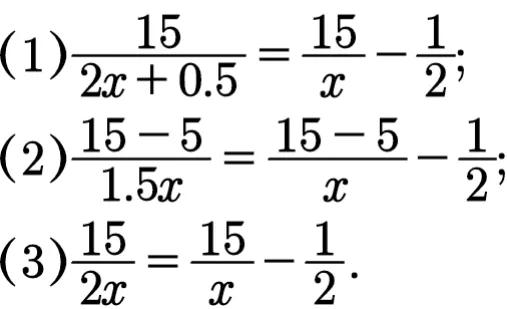
(2)我们还可以将本题转化为下列三题:
①A、B两地相距15千米,甲从A地,乙从B地同时出发,相向而行,80分钟后两人在距B地7千米处相遇,求甲、乙两人的速度比。
②甲、乙两人分别从相距15千米的A、B两地相向而行,甲从A地出发⅓小时后,乙从B地出发,用比甲快1千米每小时的速度行走,而两人在离B地7千米处相遇,求甲乙两人的速度。
③甲、乙两人分别从相距15千米的A、B两地同向而行,已知甲速度比乙速度快1.5千米每小时,若甲先走⅓小时后,乙从B地出发,问经过几小时甲可以追上乙?
(3)我们还可以将本题转化为工程问题。
例如,甲、乙两人各加工同一种零件15个,甲比乙每小时多加工1个零件,若他们同时开始加工,结果甲比乙提前半小时完成,问甲乙两人每小时各加工多少个零件?
我们可以看出,本题与工程类应用题的解题思路和所列方程是一致的,只需将路程改成工作量,速度改成工作效率,走路的时间改成工作时间即可。可谓是“百川入海,殊途同归”。

