两千多年前，中国古人就对浩瀚宇宙进行了探索，并记录于典籍《周髀算经》之中。这本书不仅记载了古人测量天高地广的方法，还计算了太阳的大小和远近。本文将带您一起探究《周髀算经》中蕴藏的古代智慧。
一、天有多高？——“立表测影”法《周髀算经》认为天与地彼此平行，太阳在正午时悬挂于天际。因此，只要测量出正午时太阳离地面的高度，就能推算出天与地之间的距离。测量方法的核心是“立表测影”。在地面上竖立一根杆子，称为“表”或“髀”。阳光照射在表上，会在地面上投射出影子。古人发现，表的位置越靠南，影子越短；越靠北，影子越长。《周髀算经》中记载：“立表八尺，勾之损益寸千里。”意为：表高八尺，影子长度（勾）的变化与表南北移动的距离成正比。具体来说，表南移一千里，影子缩短一寸；北移一千里，影子增长一寸。
通过数学方法可以证明这一结论。假设太阳光在地面的投影点为A，A点到表的距离为L，太阳到地面的距离为H，表高为h。根据相似三角形原理，可以得出比例关系：h/H = 影子长度/ (L + 影子长度)。由于太阳高度H远大于表高h，可以简化公式为：影子长度 ≈ (h/H) L。因此，影子的长度与L成正比，即表的位置变化会引起影子长度的均匀变化。根据“寸千里”的记载，当表高为八尺（h），位置变化一千里（ΔL）时，影子长度变化一寸（Δ影子长度）。由此可以计算出天高H：H = (1000里 8尺) / 1寸 = 8万里。当然，由于地球是球形而非平面，“寸千里”的结论并不准确。然而，在古代认知条件下，这种测量方法体现了古人的智慧和探索精神。
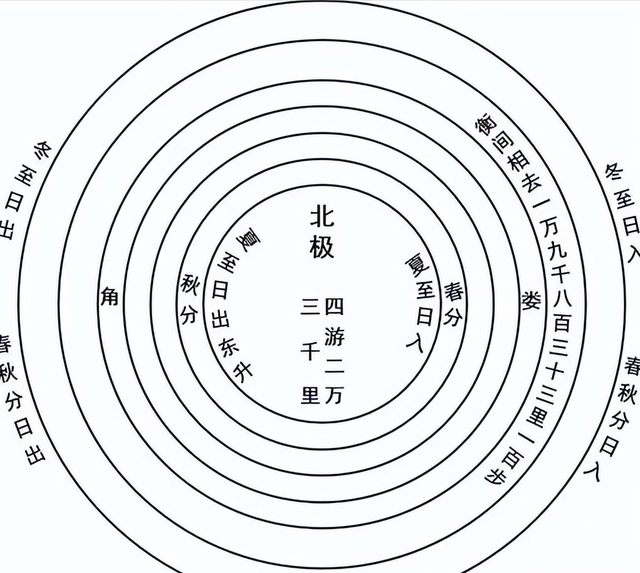二、太阳有多大？——陈子测日除了测量天高，《周髀算经》还记载了陈子测算太阳大小的方法。陈子同样利用“立表测影”的原理。他选择表高八尺，影子长度六尺的时刻进行测量。此时，根据勾股定理，表顶到影子顶端的距离（弦）为十尺。由于已知天高为八万里，根据相似三角形原理，可以推算出太阳到表的距离约为六万里，太阳到观测点的距离（S）约为十万里。
接下来，陈子用直径一寸、长八尺的竹竿观测太阳，发现太阳恰好被竹竿的两端“卡住”。这意味着竹竿的直径与太阳直径的比例，等于竹竿长度与太阳到观测点距离的比例。假设太阳直径为D，则 D/S = 1寸/8尺 = 1/80。由此可以计算出太阳直径：D = (1/80) 10万里 = 1250里。虽然由于太阳距离的测量误差，导致太阳直径的计算结果也不准确，但陈子利用相似三角形原理测量太阳大小的方法，体现了古代 astronomers 的 ingenuity.
三、盖天说：古代的宇宙模型《周髀算经》中对天高、地广以及太阳大小的测量，构成了中国古代的宇宙模型——盖天说。盖天说认为天似穹庐，地如棋盘，日月星辰在天空中运行。《周髀算经》是古代中国天文学的重要著作，它展现了古人对宇宙的探索和思考。虽然其测量方法和结论在现代科学看来存在误差，但其蕴含的科学思想和方法，对后世天文学的发展产生了深远的影响。在两千多年前，古人能够运用简单的工具和数学方法，去探索和理解宇宙，这种求知精神和智慧令人敬佩。即使他们的结论与现代科学存在差异，但这种探索精神正是科学进步的动力。从《周髀算经》中，我们不仅能看到古代的宇宙观，更能感受到古人对知识的渴望和对自然的敬畏。这或许正是这部 ancient texts 留给我们的最大价值。
