三点共线的充要条件

头条作者：冰凌花发布了一道题。

这是一道综合性非常强的几何题！难度也是相当大的！说它综合性强主要是因为它的求解过程需要用到的知识点非常多，既要画辅助线，还必须进行图形转换，还要用到一些特殊图形定理icon！非常考验同学们的综合能力！

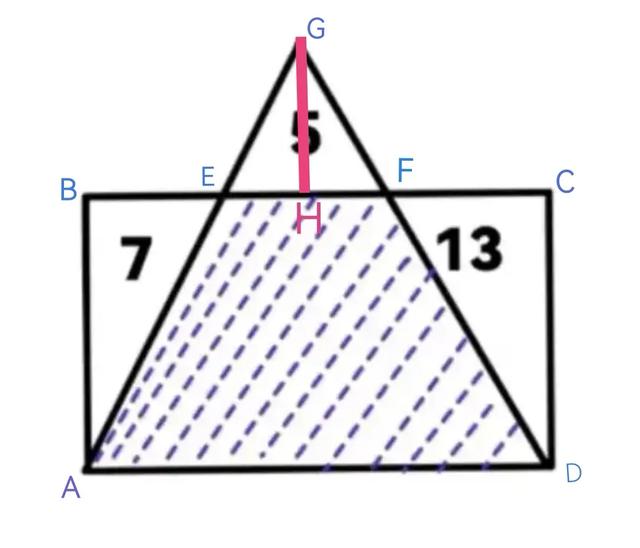
如图所示，一个长方形，从底边上两点引出线段相交于长方形外一点，已知空白三个三角形的面积分别为7、5、13，求阴影部分面积？

以上内容引自冰凌花的头条。

问题图画的比例失调，容易误导读者。我们可以通过计算求出图形顶点坐标，从而画出正确的图形。

解题思路：欧几里得的解题工具箱有两大法宝，即全等和相似。

把原文的问题图标注字母，得到下图。

解法一

从E和F分别向底边AD作垂线，就得到面积分别为7和13的三角形，它们与图中对应的三角形全等。

从G点作垂线，垂足是H，就得到两对相似三角形。

因为等高三角形面积之比等于底之比，所以有BE:FC=7:13，从而有EH:HF=7:13。已知三角形EFG面积为5，平均分为20份，那么三角形EHG分得7份，而三角形FHG分得13份。所以三角形EHG面积为5×(7/20)=7/4，同理可证三角形FHG面积为13/4。

我们发现三角形FHG∽三角形FCD，面积之比等于1:4，(相似三角形的面积之比等于相似比的平方)那么相似比为1:2。

同理可证，三角形EHG∽三角形EBA，相似比也是1:2。

阴影面积是一个梯形面积。从上底向下底作垂线，就把梯形分为两个直角三角形和一个长方形。这个长方形的高等于AB=CD，宽=EF=½(BE+FC)，所以长方形面积为7+13=20。所以阴影面积=梯形面积=三角形+三角形+长方形=7+13+20=40。

解法二

我们现在来求A，B，C，D，E，F，G，H这八个点的坐标。

建立平面直角坐标系，设A点与坐标原点重合，坐标是(0,0)

,那么其余点的坐标为B(0,2)，C(30,2)，D(30,0)，E(7,2)，F(17,2)，G(10.5,3)，H(10.5,2)

。这是设BE=7,EH=3.5,EF=10,FC=13,AB=2,GH=1得到的坐标。

以上假设是否与题目已知条件有矛盾呢？我们来验证AEG是否三点共线，再验证DFG是否三点共线。如果两次验证都得到三点共线，那么就证明计算出的坐标符合题意，无矛盾。

三点共线的充要条件是把三点坐标代入三角形坐标面积公式，得到行列式的值为0。

首先，把AEG的坐标代入下图所示的行列式，得到行列式的值为0。这证明了三点共线。

如果三点不共线，行列式的值等于三角形面积的两倍

行列式的展开按照下图所示的对角线法则进行。

图源《数学辞海》

接下来，把DFG的坐标代入下图所示的行列式，得到行列式的值为0。结果同样证明了三点共线。这证明了我们计算出的坐标符合题意。

现在我们用三角形坐标面积公式计算三角形ADG的面积。把ADG的坐标代入公式计算得到：

S=½×(-90)=-45，取绝对值得到三角形面积为45，减去已知的三角形EFG的面积5，得到阴影面积为45-5=40。

本题的答案解析完了，总结一下。构造相似三角形是解题关键。常用的构造相似三角形的方法是平行和垂直。用解析几何的建系法解题比较明快。根据面积不能确定直角三角形的形状。既然题目不告诉你形状，说明形状不重要，出题老师不在意，那么无妨随意假设两条直角边的比例，即长宽比，就可以用建系法解题了。

科学尚未普及，媒体还需努力。感谢阅读，再见。