大家好，我是科学羊，这里是数学篇第五季第41篇。

庄子曰：“夏虫不可以语于冰者，笃于时也。” 这句话的意思是说，夏天的虫子永远无法理解冰雪的存在，因为它们的生命过于短暂，根本等不到冬天的到来。

庄子用这个比喻，暗示了人类生命的短暂以及认知的局限性。

他进一步指出：“吾生也有涯，而知也无涯。” 用有限的生命去理解无限的知识，这本身就是一件极其困难甚至不可能的事。

然而，人类的独特之处在于我们拥有超越感官世界的想象力。

虽然我们无法直接感知无限，但可以通过逻辑和推理去理解无限的某些规律。那些能做到这一点的人，其认知水平就远远超越了常人。

今天，我们再从无穷大出发，聊聊如何突破认知的局限，实现认知升级。

首先我们要知道，如果你想要把大数的模式套用在无穷大，本来就是一个错误。

想象一下，你日以夜继数数从0开始一直到无穷大。

你不停的数啊...不停的数，旁边再放一个进度条，它显示出你从0%到100%的实时进度。

你觉得会像上面这个动图一样，从0到100会如实填满吗？

答案是：不可能！

那你这个进度条会呈现怎样的状态呢？

是这样，即使你已经数到了一百万，这个进度条仍然会让人沮丧地停留在0%。为什么会这样呢？

因为相比无穷大，你数到的一百万几乎微不足道。

无论你数到了多大的数字，结果都不会改变。即使是数到十亿，数到古戈尔，数到“asamkhyeya”，甚至是数到古戈尔普勒克斯，进度条依然固执地停留在0%。

在无穷大的面前，所有的数字都显得渺小。任何一个数字，放在与其后续无尽的数字相比，都是微不足道的。

简单来说，在这个进度条上，所有的数字都集中在零的起点。

在0%和100%之间完全没有任何实质性进展，没有一个数字会出现在进度条的1%、50%或者95%的位置。

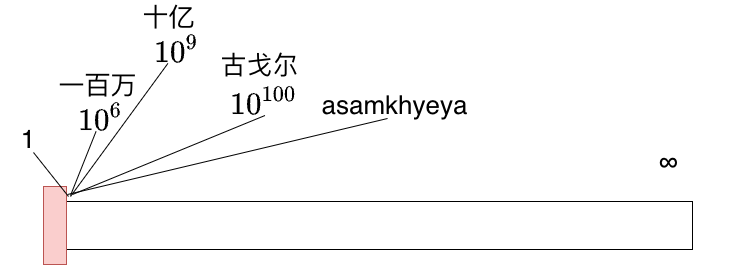
归根结底，这其实是合情合理的，因为无穷大的一半依然是无穷大。如果你的进度条走到了所谓的“中间”，那实际上已经意味着它到达了终点。

好，既然知道了基本概念，我们来看看实际的应用问题。

01 数字的较量：从儿童的游戏到无穷大的世界

小孩子们喜欢比谁说出的数字更大，一个孩子说一百，另一个孩子马上说一万，接着又有人问：“一万到底有多大？”

这个问题的答案很简单：“一万就是一百个一百。”

于是，一百说不过一万，比赛结束。

然而，过不了几天，输了的孩子回去问家长，得到一个新的答案：一亿。

他回到伙伴们面前，又赢回了胜利。

但游戏并不会就此结束。如果孩子们继续追问，最终，他们会接触到“无穷大”这个概念。

这个概念会让任何想继续较量的大数字游戏戛然而止。无穷大似乎打破了所有的规则——这是一个没有尽头的数字，谁也无法超越。

但无穷大到底是什么？

它真的是一个数吗？

它在数学上可以和其他大数字相比较吗？

02 无穷大的哲学与数学思考

在大多数人心中，无穷大是一个非常非常大的数字，只不过比我们能想到的任何数字都要大得多。

然而，这种理解其实非常片面。

无穷大的世界和我们日常认知的世界有着本质的区别。

1924年，德国数学家大卫·希尔伯特提出了一个著名的“旅馆悖论”，帮助人们重新思考无穷大的本质。

他假设有一家拥有无限房间的旅馆，所有的房间都住满了客人。

这时，如果再有新的客人到来，老板能为他安排房间吗？令人惊讶的是，答案是肯定的。老板只需让1号房的客人搬到2号房，2号房的客人搬到3号房，以此类推，1号房便空出来了。

这不仅能安置一个新客人，甚至可以接纳无限多的新客人。

这个悖论看似荒谬，但它揭示了无穷大的奇妙之处：在有限的世界里，所有房间都满了就代表无法再接纳新客人；

但在无穷大的世界中，有限的思维和规则不再适用。在这里，部分和整体可以是相等的，无穷大加一仍然是无穷大。这种反直觉的逻辑，令我们重新审视自己的认知边界。

03 数学世界的无穷：动态而非静态

通过希尔伯特的旅馆悖论，我们可以明白，无穷大不是一个简单的、具体的数字，而是一种动态的趋势。它代表了无限扩展、永无止境的变化。

数学家们在探索无穷大的过程中，逐渐发现了更深层次的规律。

例如，5厘米长的线段与10厘米长的线段，虽然在日常经验中我们知道前者更短，但在线段上的点数目上，它们是相同的。

这个令人震惊的结果表明，在无穷大的世界中，某些直观的结论可能需要重新审视。

不同类型的无穷大也是可以比较的。

举个简单的例子：10厘米线段上的点数要比所有有理数的个数更多。这种比较颠覆了我们对数量的基本理解，但它是数学上的真实结论。

总结：

从无穷大的世界观中，我们得出了一个重要的启示：在有限的认知框架下，我们无法真正理解无限的事物。许多人凭借有限的经验，得出错误的结论。