我们一起来推导一下自然数前n项立方和公式。这个公式的结论如下：
立方和=和的平方
1³+2³+3³+······+n³=(1+2+3+······n)²
注意：必须是从1开始的连续自然数，才成立！
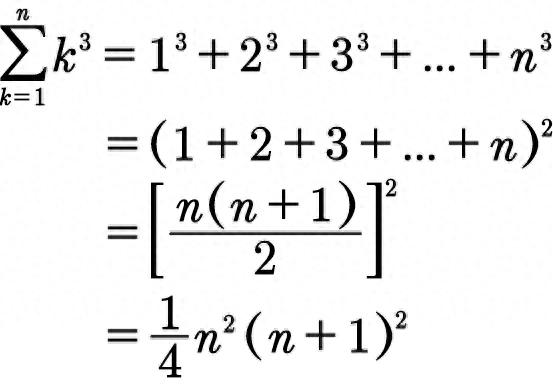
自然数立方和公式
人的正确思想是从哪里来的？
毛泽东认为人的正确思想，只能从社会实践中来。
毛泽东在《人的正确思想是从哪里来的？》一文中指出：“人的正确思想是从哪里来的？是从天上掉下来的吗？不是。是自己头脑里固有的吗？不是。人的正确思想，只能从社会实践中来，只能从社会的生产斗争、阶级斗争和科学实验这三项实践中来。”这强调了实践对于认识形成的基础性作用。
我们来探究一下公式是如何发现的。
首先给出公式的无字证明。
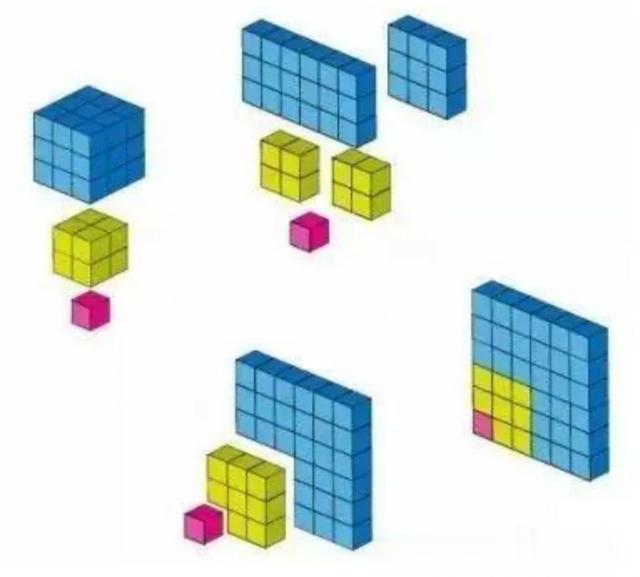
上图的三个立方体显然是代表1³，2³，3³，然后分割，再重新组合，巧妙地证明了1³+2³+3³=(1+2+3)²。这个证明展示了降维打击的威力，像玩拼图游戏一样，优雅地证明了自然数立方和公式。
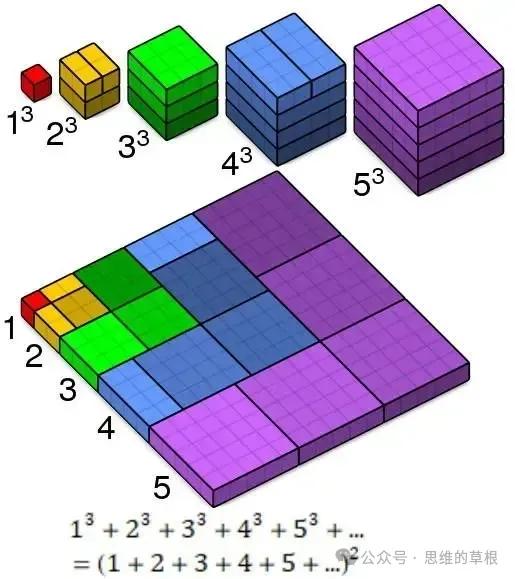
公式也可以从下图所示的表格中归纳总结出来。
微信视频号截图
表格很有规律，每一行都是等差数列。
第一行等差数列的公差是1，第二行等差数列的公差是2，
......
第n行等差数列的公差是n，
而且，这些数列的通项公式分别是aₙ=n，aₙ=2n，aₙ=3n，以此类推。
公式的推导请大家自己看图就明白了。
现在让我们用公式解决一道数学竞赛题。
题目呈现
今天是星期日，若明天算第一天，则1³+2³+3³+...+1995³天是星期________。
(1995年上海初中数学竞赛题)
解：∵1³+2³+3³+...+1995³
=(1+2+3+...+1995)²
=(1995×998)²
因为1995=3×5×7×19，即1995能被7整除，所以(1995×998)²也能被7整除，
故1³+2³+3³+...+1995³能被7整除。
已知今天是星期日，明天是星期一，所以第1³+2³+3³+...+1995³天是星期日。
特别收录
美国中学数学课本讲解求和符号
中文翻译：
西格玛符号（求和符号）
写出一个数列可能会很耗时且冗长。为了方便起见，有一种更简洁的符号，叫做西格玛符号（求和符号）。数列3 + 6 + 9 + 12 + … + 30可以表示为 \sum_{n = 1}^{10}3n。这个表达式读作“当n从1到10时，3n的总和”。
（有一个图示标注了西格玛符号的各个部分：“n的终值”、“数列项的公式”、“n的初值”）
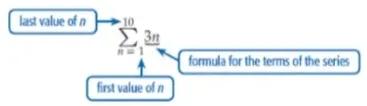
变量（在此例中为n）被称为求和指标。
要得到用西格玛符号表示的数列的各项，依次将求和指标用从该指标初值到终值（包括初值和终值）之间的连续整数来替换。对于上述数列，n的值依次为1、2、3，依此类推，直到10。
表示一个给定数列的方法有很多种。如果改变变量的初值和终值以及数列项的公式，也可以得到相同的数列项。例如，以下表达式产生相同的数列项。
\sum_{r = 4}^{9}(r - 3)
\sum_{s = 2}^{7}(s - 1)
\sum_{j = 0}^{5}(j + 1)
英文原文：
Sigma Notation
Writing out a series can be time - consuming and lengthy. For convenience, there is a more concise notation called sigma notation. The series 3 + 6 + 9 + 12 + … + 30 can be expressed as \sum_{n = 1}^{10}3n. This expression is read the sum of 3n as n goes from 1 to 10.
[Diagram showing parts of the sigma notation: "last value of n", "formula for the terms of the series", "first value of n"]
The variable, in this case n, is called the index of summation.
To generate the terms of a series given in sigma notation, successively replace the index of summation with consecutive integers between the first and last values of the index, inclusive. For the series above, the values of n are 1, 2, 3, and so on, through 10.
There are many ways to represent a given series. If changes are made to the first and last values of the variable and to the formula for the terms of the series, the same terms can be produced. For example, the following expressions produce the same terms.
\sum_{r = 4}^{9}(r - 3)
\sum_{s = 2}^{7}(s - 1)
\sum_{j = 0}^{5}(j + 1)
科学尚未普及，媒体还需努力。感谢阅读，再见。
