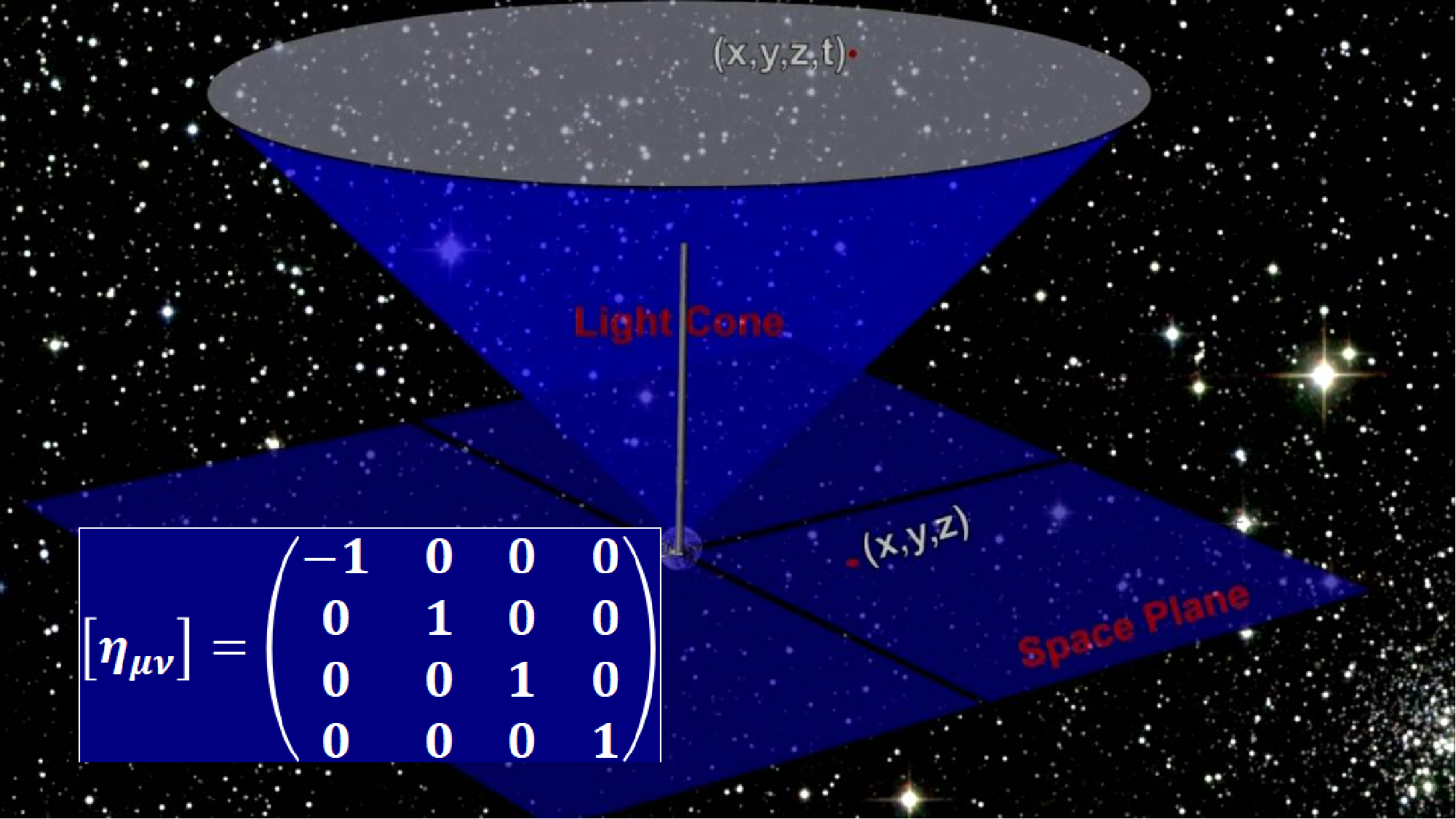
正如我们在欧几里德几何看到的一样，度规是一个定义特定空间中两点之间距离的函数。一旦我们知道了空间的度规，我们就知道了（至少在理论上）关于空间几何的一切，这就是为什么度规是至关重要的。

回想一下欧几里德度规是：

这是时空两点之间距离的函数的一种形式，时空间隔由下式给出：

如果将区间Δs、Δt、Δx、Δy和Δz设为无穷小，则得到坐标微分ds、dt、dx、dy、dz，可以用它们来定义闵可夫斯基i线元：

式1

正如我们在定义欧几里德度规时所做的那样，我们使用闵可夫斯基线元素的度规系数来定义闵可夫斯基度规，它表示为：

从式1中，我们可以看到以下几项：

所以度规系数是+1，-1，-1，-1，我们可以排列成一个4 × 4矩阵

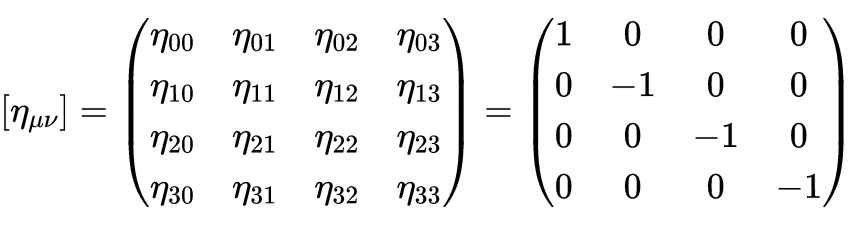
这个矩阵简单地告诉我们如何乘微分dt, dx, dy, dz得到线元。我们可以把矩阵写成表格

我们看到，dt × dt = 1，dx × dx = -1，dy × dy = -1，dz × dz = -1，所有其他的乘积都等于0。

η符号后的指数μν通过参考矩阵的行和列来识别矩阵的元素。约定是度规系数从0到3。因此

等等。

我们可以使用指数符号和爱因斯坦求和约定更简洁地重写闵可夫斯基线元素（式1）

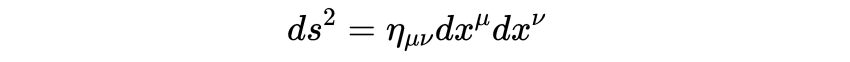
式2

其中

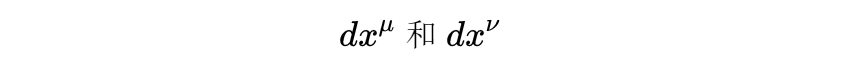
是坐标微分dt，dx，dy，dz。使用类似的符号，我们可以将时空区间∆s^2改写为：

式3

其中

表示四个时空分量ct，x，y，z。在上一篇文章中，我们看到固有时可以用时空分离表示：

因此，使用指标表示法，我们可以用度规张量表示固有时为：

用线元表示为：

式4

度规张量中正号和负号的构型称为度规符号。在本文中，我们使用度规符号+ - - -。一些教科书使用相反的度规符号- + + +，这意味着他们会把闵可夫斯基度规写成：

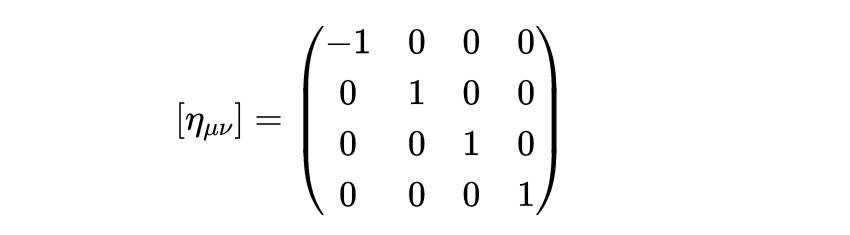
使用哪种约定并不重要只要计算时符号一致就行。

以上所有假设我们使用的是笛卡尔坐标。当然，我们可以用任何坐标系来描述时空中的事件，只是笛卡尔坐标系通常是最直接的。在球坐标下，闵可夫斯基线元为：