物理学在很多方面都是关于对称性的。正如我在以前的文章中多次提到的,一个物理系统的对称性决定了它的许多属性。这些属性之一是一个系统所具有的守恒量。例如,如果一个物理系统具有旋转对称性,那么其物体的旋转动量是守恒的。同样,如果一个系统具有平移对称性,那么在一条直线上运动的物体的动量也是守恒的。
到目前为止,守恒量还不是现代物理学中对称性的唯一用途。我了解到的一个令人惊讶的概念是对称性在创造粒子本身中的作用。这个过程被称为自发对称性破缺(spontaneous symmetry breaking),它是描述粒子为什么有质量的最佳机制。在我详细介绍之前,我先简单地解释一下:在低能量下,一个系统可能会从一个对称状态突破到一个非对称状态。当这种情况发生时,我们会发现奇怪的、短暂的粒子突然出现, 虽然这种机制被用于研究高能理论物理学,但它也广泛适用于像磁铁这样熟悉的东西。
朗道-金兹堡模型(The Landau-Ginzburg Model)一个物理系统通常用一个拉格朗日量(函数)来描述,即系统的动能和势能之和。例如,如果势能看起来是圆柱形或漏斗形,那么拉格朗日量可能拥有旋转对称性,因为旋转它不会产生任何影响。另一方面,如果我们看一个有大量能量的系统,拉格朗日量的对称性往往被保留下来。
为了解释这一点,我们将研究一种控制磁性材料中原子集合的机制。这一机制最初是由物理学家金兹堡和朗道提出的。首先,他们为磁性材料定义了一个拉格朗日量,旨在捕捉其关键特征。拉格朗日量是对物理系统的信息进行紧凑编码的一种方法,通常是根据系统的对称性进行猜测。拉格朗日公式是这样提出的。我也写了一个定性的版本,使它更容易阅读。

由于他们想描述许多不同粒子的集体行为,拉格朗日量不只是代表一个单一的粒子,而是一个场。场在上面的表达中用希腊字母phi表示。场指的是在空间的每一点都有属性的物理对象,比如房间里的温度。拉格朗日量中的第一个项描述了场本身的动能。他们还包括一个类似于某种 "质量 "属性的术语。这就是拉格朗日量的第二个项。最后一个项旨在描述粒子之间的相互作用,这些粒子之间的相互作用强度用数字λ(lambda)来表示。
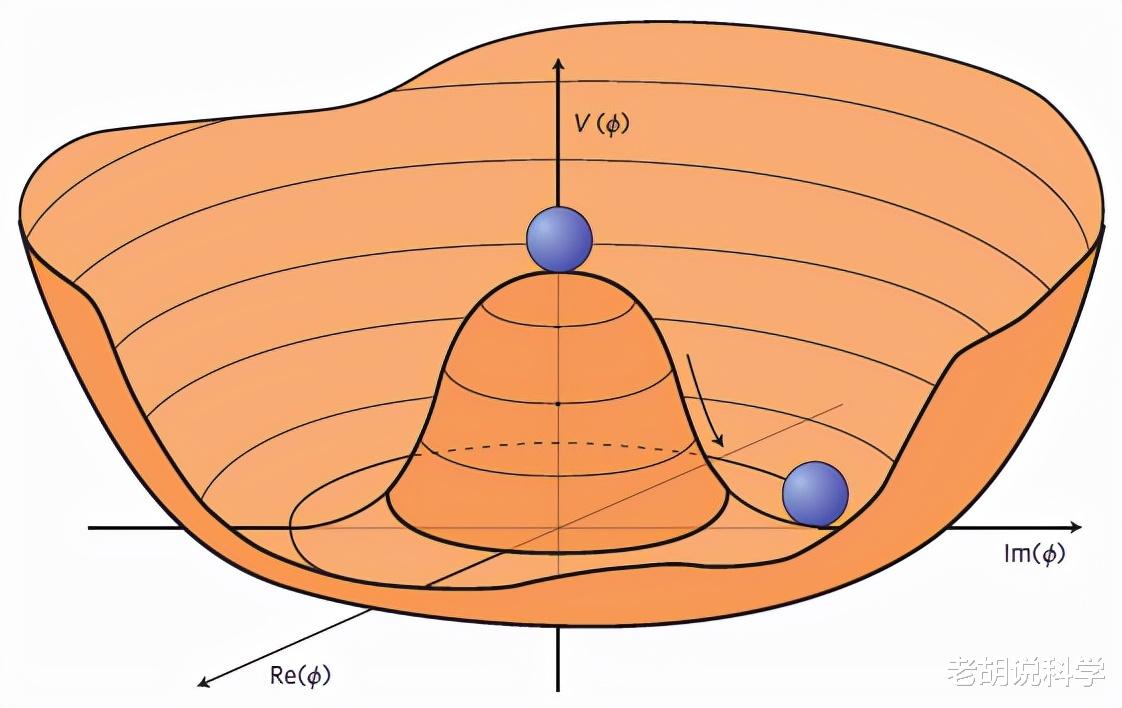
当场具有正质量时,拉格朗日量看起来就像下图中的势阱(potential well),在这种情况下,场的"稳定状态 "位于这个势阱的底部。物理学家把这称为基态(ground state)。在正质量的情况下,基态发生在场值等于零的地方。在这样的物理问题中,我们所做的一切几乎都与基态有关。

朗道和金兹堡随后提出了一些迷人的问题,从这个拉格朗日量中得到一些令人兴奋的物理学。例如,当我们降低系统的温度时会发生什么?由于在这个拉格朗日量中没有明确的温度项,我们如何能将其纳入其中呢?第一个猜测是尝试使质量取决于温度。所以他们创建了一个模型,根据温度是否足够冷,质量突然变成负数。

负质量是什么意思?在爱因斯坦的狭义相对论中,一个物体的质量和它的速度之间存在着一种关系。这种关系被称为能量-动量关系:

这种关系告诉我们一些基本的东西。首先,它告诉我们,在任何惯性参考系下,具有正质量的粒子都不能超过光速。它还告诉我们,零质量的粒子必然以光速飞行。这就是为什么光子,一个离散的光包,没有质量。最后,它还说,具有负质量的粒子必须比光速更快。这些类型的粒子被称为超光速粒子(tachyons),它们超越了物理学中的任何因果关系的概念。
因此,当温度足够低时,就会有超光速粒子冒出来。正如我所说,这个理论中的 超光速粒子的存在是一个问题。
为了解决这个问题,朗道和金兹堡改变了拉格朗日量,改变了质量的符号。质量变成负值的温度被称为临界温度。事实证明,当温度足够低时,势能就会倒转,最低点也会改变。在上面的例子中,只有一个最低点。在这种情况下,现在有两个最低点,在场值为零的区域类似于一个 "山丘"。

该图显示了可能发生的两种情况。在左边,是温度高和质量为正的情况。在右边,是温度低的情况。在零点会发生什么?山顶上的这个区域是不稳定的,可以看到,如果我把这个不稳定的山顶上的粒子(右图中的黑点)稍微扰动一下,它就会随机地掉落到两边的底部。因此,在高温下作为基态的那一点现在已经变得不稳定,被两个较低的基态所取代。
从单一的基态到两个可能的基态就是 "对称性破缺 "的全部内容。当温度足够低时,物理系统必须选择一个解——X轴右边的正基态或左边的负基态。以前,拉格朗日量并不关心任何意义上的 "正 "或 "负 "符号。现在,对称性在低温下被打破了,它必须在两种可能的基态之间做出选择。这就是对称性打破机制的核心。
戈德斯坦玻色子(Goldstone Bosons)现在,系统中有了一些被打破的对称性。我们如何从中产生一个粒子呢?由于拉格朗日量最初是对称的,诺特定理(Noether's theorem)指出,有一个与对称性相关的电荷。例如,量子电动力学中的对称性导致了我们现在所知的电荷。当你用这种电荷激发这些基态之一时,实际上可以得到一个没有质量的粒子从中漂浮出来,就像光子一样!这些无质量的粒子,来自于一个没有质量的地方。这些来自对称性破缺的无质量粒子被称为戈德斯坦玻色子。这些戈德斯通玻色子不会出现在不稳定状态下,只出现在对称性被打破的基态上。

张得帅
一个物理系统通常用一个拉格朗日量(函数)来描述,即系统的动能和势能之和。例如,如果势能看起来是圆柱形或漏斗形,那么拉格朗日量可能拥有旋转对称性,因为旋转它不会产生任何影响。另一方面,如果我们看一个有大量能量的系统,拉格朗日量的对称性往往被保留下来。 …… 由于他们想描述许多不同粒子的集体行为,拉格朗日量不只是代表一个单一的粒子,而是一个场。场在上面的表达中用希腊字母phi表示。场指的是在空间的每一点都有属性的物理对象,比如房间里的温度。拉格朗日量中的第一个项描述了场本身的动能。他们还包括一个类似于某种 "质量 "属性的术语。这就是拉格朗日量的第二个项。最后一个项旨在描述粒子之间的相互作用,这些粒子之间的相互作用强度用数字λ(lambda)来表示。 …… 这种关系告诉我们一些基本的东西。首先,它告诉我们,在任何惯性参考系下,具有正质量的粒子都不能超过光速。它还告诉我们,零质量的粒子必然以光速飞行。这就是为什么光子,一个离散的光包,没有质量。最后,它还说,具有负质量的粒子必须比光速更快。这些类型的粒子被称为超光速粒子(tachyons),它们超越了物理学中的任何因果关系
吞噬黑洞再造宇宙
这个势能怎么来的? 时空和动能动量互为参数,局域空间非线性造成能量约束形成基本粒子,这是本质来源。 这种非线性方程没有人会解!
吞噬黑洞再造宇宙 回复 10-26 17:40
标准理论中的参数都是手加上去的!基本常数,粒子内禀参数,哪一个是理论中算出来的? 宇宙方程,不需要用手加入一个参数,可惜人看不到这个方程,更不会解。
连杰12
好文分享一下你的时候,
用户13xxx60
这种波色子被探测到了吗
元道
好
用户13xxx60
神之领域
我净常乐
感觉文章没说完啊。所以粒子质量到底怎么来的?