“我们鼓励你去开发程序员的三大美德:懒惰、不耐心和傲慢”--via ranganwald.com

larry wall
懒惰和热忱
在计算机领域,“懒惰”是一个广义的术语,一般是指不得已的情况下是不做任何工作的。其反义词是“热忱”,意味着尽可能的做大量的工作以备将来需要。
简单介绍了两个单词后,我们看这么一段JavaScript代码:

好 的,这里有个问题:在上面的代码中,JavaScript计算2+3了吗?你可能已经知道答案了——是的,上面的代码中确实计算了2+3。 JavaScript是“热忱”的,当调用ifThen方法并传入参数时,不管表达式的值是否被使用,它都计算了所有的表达式。(注1:有些人指出足够聪 明的编译器可以注意到2+3涉及两个常量和一个固定的操作符,然后可以将其提前编译成5。JavaScript并不一定执行此优化,但是如果确实执行了, 我们仍可以用x+y来替换文中的表达式来得到相同的结果。)
假设 说,JavaScript是懒惰的,则不会在表达式ifThen(1===0,2+3)中计算2+3的值。所以JavaScript是一种“热忱”的语言 吗?可以这么说,但不总是如此!如果我们这么写表达式:1 === 0 ? 2 + 3 : undefined ,JavaScript便不会计算2+3。像?:、&&、||还有程序结构控制语句if,都是“懒惰的”。你只需要在脑子里记住哪些是热 忱的,哪些是懒惰的就好。
如果你想要一些懒惰的做法,而这些操作本身天生并不是懒惰的,你需要围绕JavaScript的热忱做些工作,比如:

JavaScript会急切的计算()=> 2+3,因为这是一个函数。但是并不会在函数内部的表达式中进行计算,直到被调用时才会进行计算,只要不被调用,2+3就不会被计算。
产生懒惰
函数体有些懒惰:它们直到真正调用函数时才会执行计算。这跟if语句,和其他任一种结构化控制语句一样。 JavaScript不会计算语句除非代码真正执行到这部分语句。
考虑下面的代码:

毫无疑问,你极有可能会嘲笑上面这段天真幼稚(na?veté)的代码。假设有这么一个包含从1到10亿的列表,如[1, 2, 3, ..., {{999999998:0}}, {{999999999:0}}, {{1000000000:0}}],我们调用上面的方法:

虽然我们得到了正确的结果,但是我们首先遍历了列表中的每一个数字,这可是10亿个数啊,这段代码简直太差了,连小孩子估计都会知道我们可以JavaScript函数中的添加return来规避剩下的不必要的操作,即我们可以这么写这段代码:

修改后的程序版本比第一个更“懒惰”:为了判断指定列表中是否包含某个值,这段代码只做必须做的,从而尽可能减少不必要的操作。
从函数containing引伸出来,我们可以写一个类似的方法,findWith:

findWith使用了一个谓词函数来偷懒地查找列表中的第一个值。不幸的是,尽管上面提到的findWith是懒惰的,它的参数却热切的进行了计算。好,现在假设说我们想找到列表中的第一个大于99并且是回文的数字:
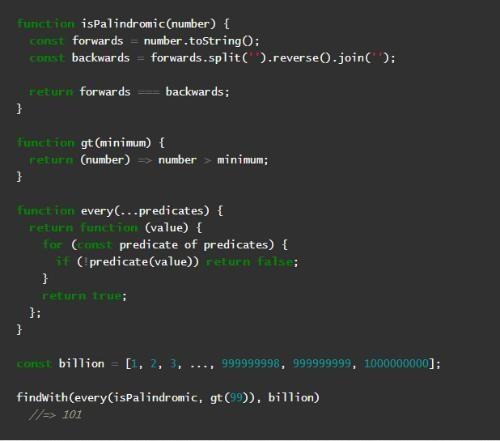
这里的机制和上面提到的一样,当然,我们在遍历10亿个数字时,只要遇到第一个大于99且是回文的数字遍停止执行。
但是,JavaScript热切的计算了findWith的参数。即,计算了isPalindromic, gt(99))并将其绑定到predicate,所以实际上还是计算了列表中的10亿个数字。
将值绑定到另一个变量上开销不大,但是如果我们不得不生成10亿个数字呢?如下代码所示:

NumbersUpTo({{1000000000:0}})是个热心肠的函数,尽管我们只需要一个101,它依然产生了一个10亿个数字的列表。这就是个问题了:我们想在整个统计计算过程中一直保持懒惰。
幸运的是,我们刚刚完成了一个生成器,所以我们知道如何准确的创建一个懒惰的列表。

此 时,生成器用懒惰的方式产生数,findWith用懒惰的方式查询,这样,我们就可以在没有生成那些无休止的数字的情况下找到 101.JavaScript仍然热情的计算Numbers(),并将其绑定给list,但是现在是绑定了一个迭代器而非数组。至于for (const element of list) { ... }语句,则以偷懒的方式在迭代器中取值,就像我们前面提到的那样。
埃拉托斯特尼筛法
埃拉托斯特尼筛法是一种简单且年代久远的算法,用来找出一定范围内所有的素数。
我们有一张写满数字的表哥(如,2、3、4、5...),逐渐以某种规则划掉表格中的数,则剩余的数字就是素数。特别的,我们以某个数字P开始,则:
声明P是素数,则在表格中划掉P的倍数,从P的平方开始,依次往下;
划掉P的所有倍数后从P的下一个未被划掉的数字开始,将这个数字复制给P,并重复步骤一。
下面是埃拉托斯特尼筛法以“热情”的方式所写的代码实现:

接下来,让我们用懒惰的方式来写,首先,使用一些我们在本文和JavaScript Allongé中已经说明过的操作:

有 了这些,我们可以在此基础上写一个生成器,将一个迭代器映射到一个包涵数值的序列上,这个序列的每个第n个元素都变成null。(注2:这是根据书面描述 的最简单和最天真的实现方法,在The Genuine Sieve of Eratosthenes中,Melissa E. O'Neill描述了如何写一个比这种实现方式更快的懒惰的筛选函数,尽管他抽象化了从表中划掉倍数的概念)
这就是筛选行为的核心思想:将数字列表最前面的数字设为n,筛选掉后面n的每个倍数元素。
现在,我们可以递归的应用nullEveryNth:取待筛选列表中的第一个数字,筛选掉它的倍数,然后将剩下的数字作为结果产出:

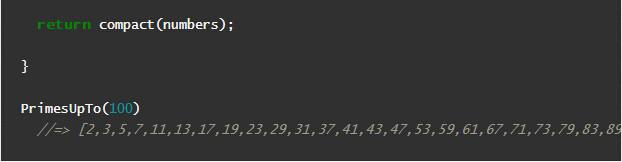
有了这个sieve函数,我们可以使用range函数来得到一个从2开始的数字序列,递归的进行筛选,然后调用compact将所有的nulls过滤掉,剩下的就是素数了:

除了性能之外,你有没有发现其它明显bug?你可以试着运行一下,上面这段代码是无法运行的。问题在于最后一步,我们调用的compact是一个热切的方法,并不是一个懒惰的函数。所以我们在过滤掉空之前就开始尝试创建一个无限的素数列表。
我们需要写一个compact的懒惰版:

现在,大功告成啦!
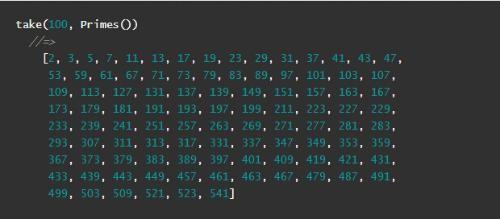
当我们以懒惰的风格写东西的时候,我们需要所有常用操作的懒惰版本,比如,下面是unique的热情版实现:

自然的,如果我们想通过一个偷懒的迭代器找到不重复的数值,则需要一个懒惰版unique实现:

这个操作贯穿列表的整个操作过程:我们想要一个懒惰版本,则需要使用迭代器,然后必须从前到后全部使用懒惰的操作符,这些是不能混淆的。
关于类型
上面谈到的这些内容给了我们一个意外的启示。
生成器和懒惰可以是很奇妙的。当我们尝试使用生成器来使用异步操作符模拟同步操作时,令人兴奋的事情就发生了。但是就我们看到的而言,如果我们想写一个懒惰的代码,我们必须谨慎小心的保持持续懒惰。如果我们混淆了懒惰的代码和勤劳的代码,问题就会出现。
这 是一个对称问题。更深一层讲,这里暴露了一个“鸭子类型”(Duck typing)的模式:当看到一只鸟走起来像鸭子、游泳起来像鸭子、叫起来也像鸭子,那么这只鸟就可以被称为鸭子。即通常的概念是只要对象持有正确的接 口,只要她们相应给正确的方法,则它们就是可交换的。
但不是所有情况都符合这种规 则。勤劳版本和懒惰版本的compact都在操作list的时候都可以像“鸭子”一样“呱呱”叫,但是其中一个是懒惰的,一个是勤劳的。“Duck typing”没有且不能捕捉到两者之间的区别,而正是这些区别确保了有些是懒惰的,有些是勤劳的。
很多其他的事情也于这种方式类似,比如转义和非转义的字符串,抑或是经过模糊处理和原声的ID。要区分有相同的接口,但也有语义或其他合约差异的东西,我们需要类型。
我们要确保程序的正确操作能兼容各种类型,即是不正确的操作看起来也能够时“鸭子适应”的。
