阿里巴巴全球数学竞赛的奖金总额约为30万美元。它对任何人开放，并且允许编程。下面是2021年决赛的概率与组合学赛道的第一道题。
问题
一场舞会以20个女孩和22个男孩开始，有无限多的女孩和男孩在外面等待。每轮比赛，从派对中随机挑选一个人。
如果一个女孩被选中，她邀请派对上的一个男孩跳舞，然后他们两个都离开派对。
如果一个男孩被选中，他邀请外面等待的一个女孩和一个男孩跳舞，然后他们三个都留在派对上。
当派对上只剩下（两个）男孩时，派对就结束了。
问：派对永远不会结束的概率是多少？
理解问题
选一个女孩，派对上就会少一对男女；而选择一个男孩时，派对上就会多出一对男女。
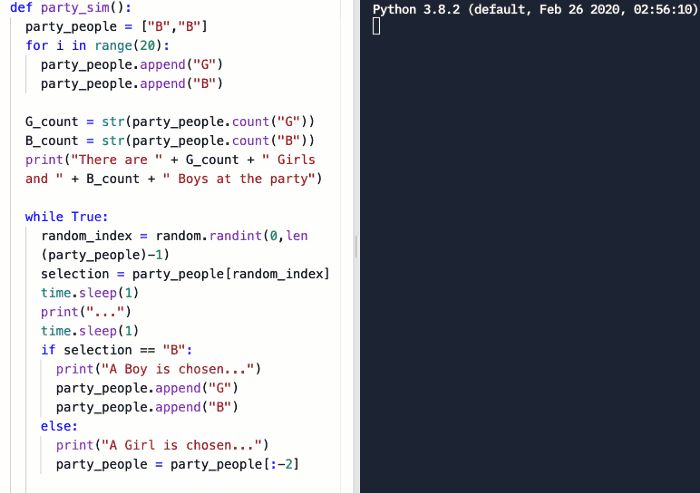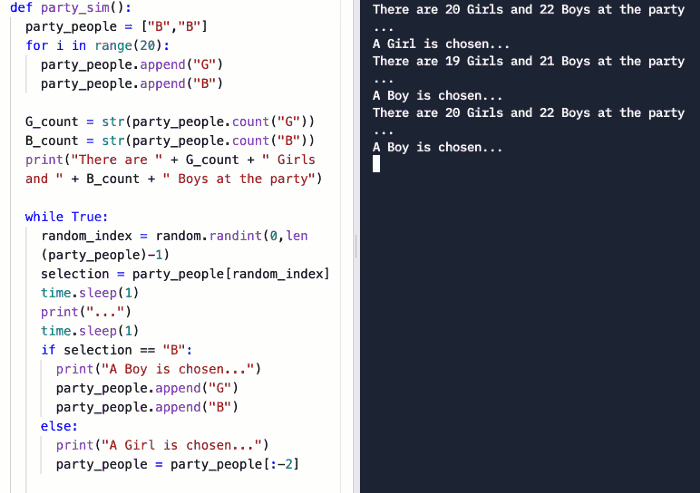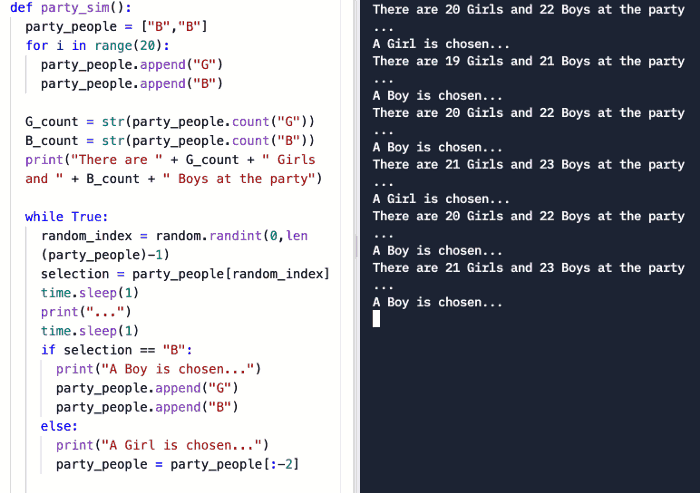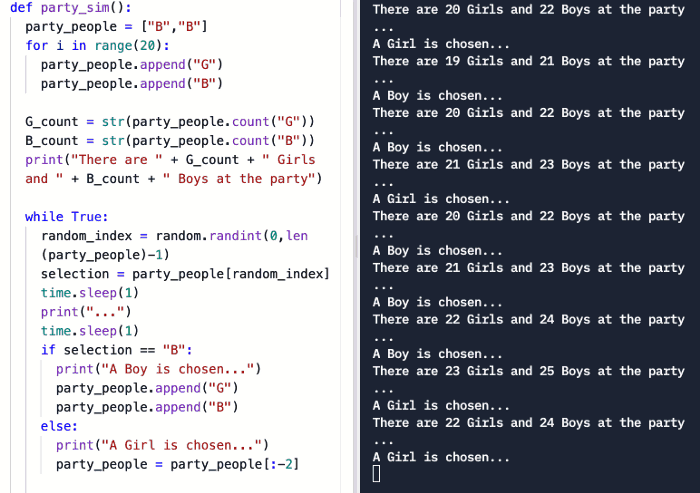
这是一个“随机游动”的例子。每轮后，从派对中选中男孩和女孩的概率都会改变。
如果还有2n人，选出一个女孩的概率是：Pr(G) = (n − 1) / (2n)
选出一个男孩的概率是：Pr(B) = (n + 1) / (2n)
我们想要求出派对“永不结束”的概率，可以计算为：
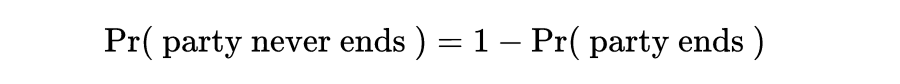
因此，我们的挑战是找出，在有限轮之后派对结束的概率。
一开始，有20个女孩和22个男孩，选出一个女孩的概率是：Pr(G) = 20 / 42
连续选出2个女孩的概率是：Pr(GG) = (20 / 42) × (19 / 40)
连续选出20个女孩的概率是：Pr(GG…G 20 times) = (20 / 42) × (19 / 40) × … (2 / 6)× (1 / 4)
消去连续的分子和分母，我们得到
连续选出20个女孩的概率太小（几乎不可能）。派对也可以在第21回合、30回合或100回合后结束。
我想简化这个问题，希望找到一些规律。
简化问题
首先，研究最简单的情况。假设这个派对只有1个女孩和3个男孩。2轮后，有三个可能的结果：
增加了2对男女
去掉了2对男女
总体上没有变化
让我们看看“没有变化”的概率，从最初的2个女孩和4个男孩开始：
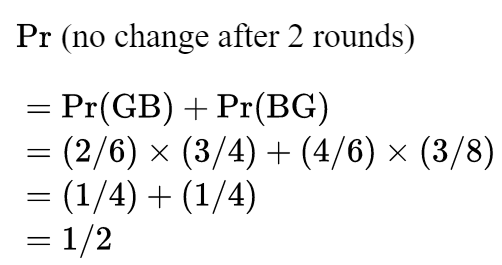
我们发现，这个1/2与剩余人数无关。如果有2n人：
然后，我们可以计算其他两种情况的概率：
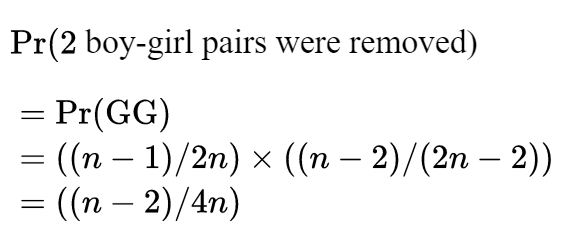
好了，现在让我们用这些规则来解决一个简单的问题：2个女孩，4个男孩的聚会结束了。
解决一个简单的情况
假设派对开始时只有2个女孩和4个男孩。所以我们只需要从派对中移除2对男女组合就可以了。
它是一个无穷级数，我假设它是收敛的（否则概率会超过1）。我们试着计算前几项开始，看看会发生什么。
（提醒一下，2n是聚会上剩下的人数。在本例中，我们从n = 3开始）。
下面，我把两个“两轮”分为一组，用“0”表示“没有变化”；“-2”表示“两对男女被移除”；“+2”表示“派对中增加2对男女”
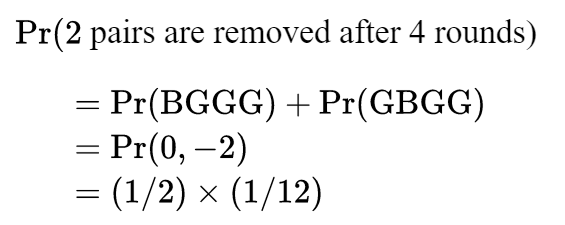
Pr(2，−2)=(1/2)^4这一事实会非常有帮助。你可以用上面的公式进行验证并简化：
到目前为止，我们已经知道：
它看起来就像一个几何级数。我们继续往下看：
其中，3 × Pr(0，2，−2，−2)中的3给无穷级数增加了一些复杂性。之所以会出现这种情况是因为有3个位置可以放置0。
寻找结构
当数字增加时，计算−2和2的排列就变得更加复杂了。看看计算4个“−2”和3个“2”的情况就知道了：
但别忘记，竞赛是允许编程的，这让求解容易了很多。
运行这个程序，我发现只包含−2和2的可能的步数如下：
1，2，5，14，42，132，…
很多人可能不熟悉这个数列，这些被称为加泰罗尼亚数字。我还发现加泰罗尼亚数字有一个简单的生成函数：
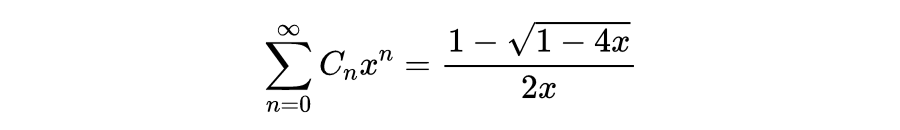
其中，C_n是第n个加泰罗尼亚数字。
研究无穷级数
这里有无穷概率级数和加泰罗尼亚数字的关系：
首先，我用上面提到的Pr(0) = 1/2和Pr(2， -2) =(1/2)^4计算单个概率。
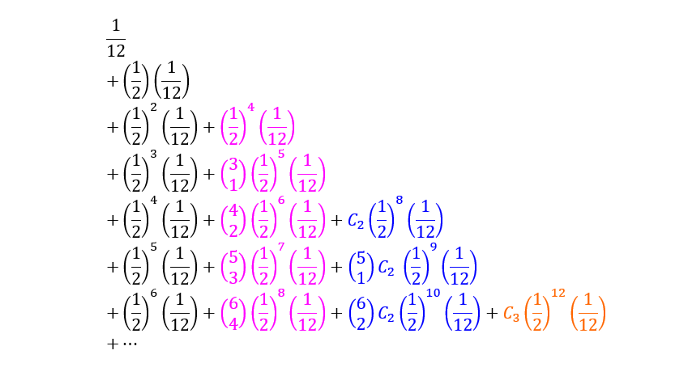
现在我们提取出公因式1/12，把它分成几个无穷级数：
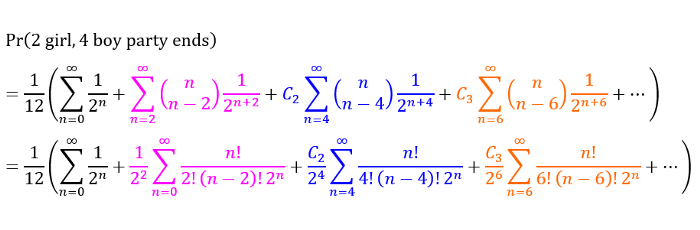
黑色级数是无穷几何级数：1 + 1/2 + 1/4 +…，它收敛于2。
粉色，蓝色和橙色的级数都有相同的结构，与加泰罗尼亚数字的生成函数相似，它们都收敛于2。
现在对每一个单独的彩色级数求值，可以应用泰罗尼亚数字的生成函数：
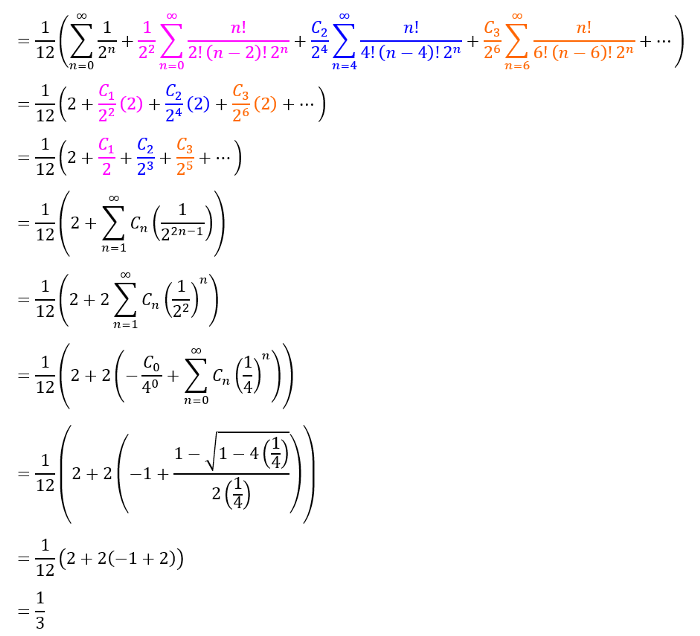
2个女孩，4个男孩的派对在有限轮数后结束的概率正好是1/3。
解决这个“更简单的问题”已经是一个漫长的过程。幸运的是，扩展这个结果以解决最初的问题并不需要太多的工作。
答案
我要解决的下一个问题是，从20个女孩和22个男孩开始，在有限的轮数之后，2对男女被移除的概率。
计算方法与上面相同，只是上面的(1/12)将被(19/84)所代替，(19/84)是n = 21时选择2个女孩的概率。
我们可以用同样的方法计算n=19的情况：
…
然后把这些概率相乘，一直到上面的1/3。因为派对结束的唯一方式就是这些事件连续发生。
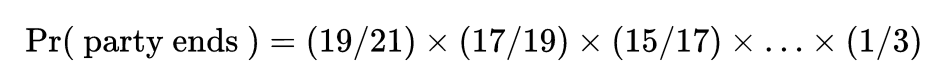
消去分子和分母就得到
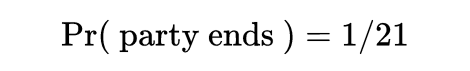
现在，问题“派对永远不会结束的概率”的答案终于出来了：
答案是：1/21。
JJ
[鼓掌]
专家
我为什么要点进来？
娱乐影视秀 回复 03-08 23:51
因为好奇
不再流浪
离谱，出题人怎么想出来的，韦神出的题么？
野生的家猫 回复 05-09 08:42
你把女生替换为潜在的消费者，场内即平台上正在浏览的用户，场外即未注册或某时刻未在平台浏览的用户，男生替换为平台上展示的商品（不喜勿喷啊），再看问题本身
建哥 回复 野生的家猫 05-12 07:43
牛逼，是这个意思。
正南齐北
搞这些数学游戏，有可能有重大意义，有可能毫无意义。问，什么情况下有重大意义。
人生若只如初见 回复 03-09 07:44
以前欧洲一个人抄底彩票，人家赚翻了，最后彩票游戏规则改了
闲谈莫论风月 回复 03-09 08:07
基础学科是一切科学发展的基础！包括数学，物理，化学
一个回忆
提到概率论我脑袋就嗡嗡的！
天下有我
我负责派对挑人，你们负责计算吧[笑着哭]
Silence℡ 回复 04-12 11:32
你挑人，我跳舞
用户77xxx29
我是来看评论区里谁能解释清楚的[呲牙笑]
韦言 回复 03-23 17:59
你这说的我想笑。这个概率模型是非古典概率和非独立事件。你这么算基本暴露出学历水平了
左左 回复 03-15 00:15
？那第一次选男的，后面联系选21个女的结束不？以此类推，前面先是男的，后面再是女的呢？你想问题太简单了吧
好冻
总概率100减去结束的概率不就是不结束的概率吗？
用户85xxx82
美国人权组织很不满，为什么剩下两个男的就结束派对？这是歧视！
用户18xxx69
完犊子了，懵逼中[笑着哭]
用户13xxx94
很明显答案是错的。应该是20／21。[呲牙笑][呲牙笑]
沧海一悦
我一个初中生点进来看了个寂寞。
深圳的辣不欢
我想知道出题者知道答案吗[笑着哭][笑着哭]
LOSS 回复 05-02 14:54
出题者一般都是逆推，即通过公式反向出题，所以说，这个题，说不定有比较简单的解法
用户15xxx62
很明显，派对只有两个结果，结束和永远不结束，那概率是二分之一[呲牙笑]
东胜
现实派对一定会结束[得瑟]
心如止水。
搞脑子是吧，搞脑子是吧，我承认我不会。
包子头
概率论就考了60分，你看我有资格看这个不
半剑西来半剑东
概率论当年挂科，我居然点开来看[笑着哭]
小花
能看懂就很不错了[呲牙笑]
七月流火
看来系统还是很看得起我的，竟然给我推荐这种文章。谢谢。
狗肉汤浇地有助生长
曹
overwhelming
阿里巴巴的这个竞赛有意义[笑着哭]，能得奖就可以直接去阿里工作了[笑着哭]，他们就是为了筛选人才
梧橙
一看就知道看不明白。
新疆特产网店掌柜
[得瑟]看起来很复杂，但是结果很简单，如果倒推的话，概率就是1减去（男生22➕女生20）除以2等于21的分之一[笑着哭]哈哈，20/21。可见这个结果是有技巧的，但是正推太难[得瑟]
云阶漫步99
我进来看看评论区有没有会的[得瑟]
肥而不腻
嗡嗡嗡嗡嗡嗡嗡嗡嗡，晕死
人生路
这题目谁出的[呲牙笑]
Said
概率可以看作是重复事件里某样东西发展的极限
孤独的漫游者
这是人学的吗？
坦荡
连初中数学也搞不懂的人，我进来干什么呢？
建哥 回复 05-12 07:47
小升初的题你以为简单？
用户40xxx70
妈的我手贱点进来找虐
烟味男人
有没有大神可以算出湖北男子娶湖南女孩的概率有多少[呲牙笑][呲牙笑][呲牙笑]
精忠报国
整个UC也挑不出几个做的来的人吧
暮眼
屁话要死多，正确的答案是0。不信的话，你试个21次就知道了。别问我怎么知道的，硬币扔的我手好酸。
修身养性
概率和算命有何区别吗[得瑟]
no why
不是20/21吗？
用户16xxx40
搞这些花里胡哨的事情干什么？有钱股东就多分点，吃力不讨好的活少干
用户12xxx98
扯蛋
LOSS
看了开头和答案，啊，我懂了[得瑟]算了那么多，结果就是不管男女生数量多少，只要男生比女生多两个，那么答案就是女生数量加1分之一
冻冬
看到题目仔仔细细看了一遍，拿出一张纸，默默的写下一行数字。解：永远不会结束的概率是1 /｛（20+22）/2｝=1/21，猜的太准[笑着哭]
Kv丶
假设世界上所有人都来解答这道题。 第一问，求这一数学问题在社会面公布后，每个人解答正确的平均概率。 第二问，求一年后随机挑一个人，知道这一数学问题答案的概率。
梦回九霄
发现很多科学研究都是统计学的各种应用
野生的家猫 回复 05-09 09:17
没有统计很多理论都只能算是经验，有了统计才实现经验的从量变到质变上升为理论，但是统计思路和方法如果不对，结果也未必就正确，另外还有人能不能看懂统计结果的问题[笑着哭]
う逆あ 回复 03-09 06:42
那是必然的，很多科学的突破都是积少成多造成的，而这过程往往就和统计学有着莫大的关系
用户18xxx34
这是马尔科夫链么
墨菲斯托
十几年了，高等数学忘的差不多了[笑着哭]
用户74xxx89
答案明明是20/21，偷别人文章自己却不理解
冷眸
为什么不是挑两个女孩[吃瓜]
用户58xxx09
我何德何能[笑着哭]
灯火阑珊
还是修仙比较容易
一江春水向东流
永远不会结束的概率为0，最后总会结束的[得瑟]
用户97xxx07
结束和不结束。50%要算个毛线
一字见心
绝大部分人连题目都读不懂
黑酷
此题关键在于2女4男的情况分析，我做了一下分析，如图所示，因为纸不够写了，所以后面的就不写了[呲牙笑]
……
概率论不够，主要是组合论
Luigor
韦神直接省略过程，直接得出答案10/210
野生的家猫
你把女生替换为潜在的消费者，场内即平台上正在浏览的用户，场外即未注册或某时刻未在平台浏览的用户，男生替换为平台上展示的商品（不喜勿喷啊），再看问题本身，发现这个题目的现实意义了吗？[呲牙笑]
只爱丫头果冻
就是这个味，横看竖看都不会[笑着哭]
邪典故事会
永远不会结束的概率当然是零了！
小伙子憋跑
排列组合而已
超级大眼圈
简单，假设男女平等，概率为零。
我净常乐
这男女的意义是50%的输出或者输入，出-2入+2。题目说的是混沌系统中的一个漩涡永久存在的概率
用户13xxx27
开始说舞会，一下又比赛，莫名其妙
用户14xxx42
这解答看到我怀疑人生，不仅要编程，那个泰罗尼亚数字的生成函数我更是听都没听过，作者是真的nb
李桂
概率比高数难