在1900年的第二届国际数学家大会上，希尔伯特提出了23个问题。 我们这里感兴趣的是希尔伯特第十个问题：给定一个丢番图方程（通常是两个或多个具有整数系数的未知数的多项式方程，因此唯一感兴趣的解是整数解）如：

要求找出一个程序，运行这个程序，可以经过有限多次运算，来判定此方程是否在整数中有解。换言之，我们需要找到一个算法，使得任意给出一个丢番图方程，它都能告诉我们此方程是否至少存在一个整数解。当然，对于许多丢番图方程，很容易找到一个解，或者证明它没有解存在。然而情况并不总是这样，费马方程就是一个例子，

甚至在费马大定理得到证明以前，对任意特定的n就已经有算法存在能够决定此方程是否有解存在。

如果对于一个丢番图方程，希尔伯特的问题的答案是正面的，我们就可以拿出一个希尔伯特所要求的那一类"程序"来证明它。然而，如果想给出否定的答案，那么就得证明没有算法存在，为此就必须说明白什么才算是一个算法。

我们需要的就是算法这个概念的形式定义。早在17世纪，莱布尼兹就已经设想有一种万有的语言，使我们能够把数学证明归结为简单的计算。到了19 世纪，一批逻辑学家如巴贝奇（现代计算机的先驱者之一）、布尔、弗雷格、佩亚诺都试图通过逻辑的“代数化"来把数学推理形式化。最后，到了1931年至1936年之间、哥德尔、丘奇和克林引入了递归函数的概念。粗略地说，一个递归函数就是可以通过算法的手段来计算的函数。虽然它的基本思想可以这样粗略地表示，但是递归函数的定义却不同，它是完全精确的。

原始递归函数

递归函数的另一个粗略的定义如下：一个递归函数就是一个可以归纳地定义的函数。为了说明这是什么意思，让我们把加法和乘法考虑为由N×N到N的函数。为了强调这一点，把x+y和xy分别记成sum（c，y）和prod（x，y）。

关于乘法，有一个我们熟悉的事实：乘法就是"累加"。现在我们更精确地考察这个思想。我们可以通过下面两条规则来用函数"sum"定义函数"prod"。规则之一是 prod（1，y）= y；其二是 prod（x＋1，y）=sum（prod（x，y），y）。这样，如果知道了如何计算prod（x，y），又知道了如何计算函数sum，就会计算prod（x＋1，y）。因为又知道了如何计算"基础情况"prod（1，y），它就是y本身，再作简单的归纳论证就完全决定了函数“prod”。

我们刚才见到的就是一个函数如何用另一个函数来"递归地定义"。现在想要了解所有由 N^n到N的可以用少数几个方法建造起来的函数之类，而递归只是这少数几个方法之一。把由 N^n到 N 的函数称为n元函数。

一开始，需要有函数的一个初始的储备，其余函数都要从这个初始储备建造出来。事实表明，函数的一个非常简单的集合就已经足够了。最基本的是常值函数。就是把N^n中的任意n元组都变为一个固定正整数c的函数。另一个很简单的函数是后继元函数、它把任意正整数n变为它的后继元n＋1。这个函数已经可以生成有趣得多的函数了。最后还有投影函数：

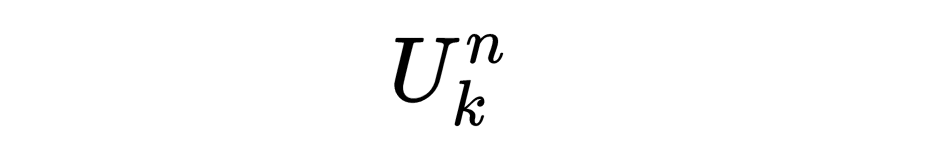
它把N^n中的（x_1……，x_n）对应为自己的第k个坐标 x_k。

然后就有两个从一个函数构造出其他函数的方法。第一个方法是代入。其意义如下：设已经有了一个m元函数φ和m个n元函数

就可以定义一个新的n元函数如下：

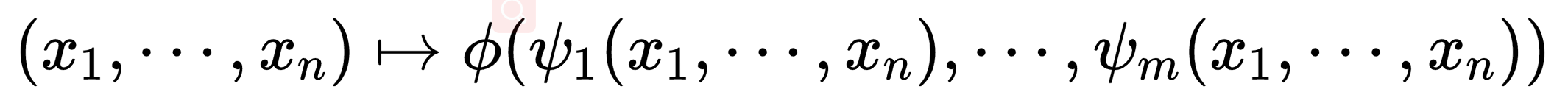
例如

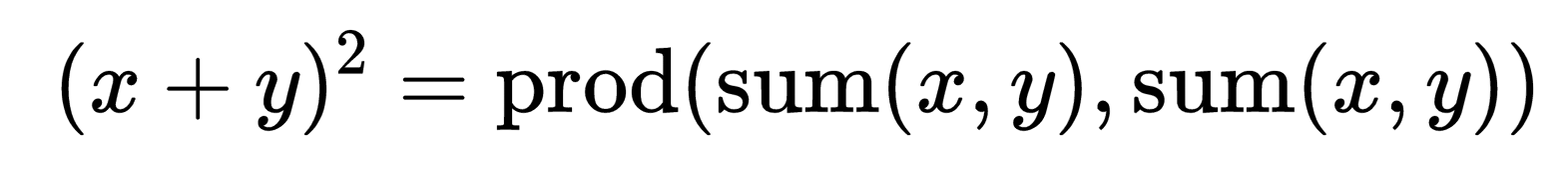
这样就从函数“sum”和函数“prod”通过代入得出了函数

第二种构造新函数的方法是原始递归，它比上面用函数"sum"来构造函数“prod”的归纳方法要更一般一点。设有一个（n-1）元函数Ψ和一个（n＋1）元函数μ，这样来定义一个n元函数ϕ：

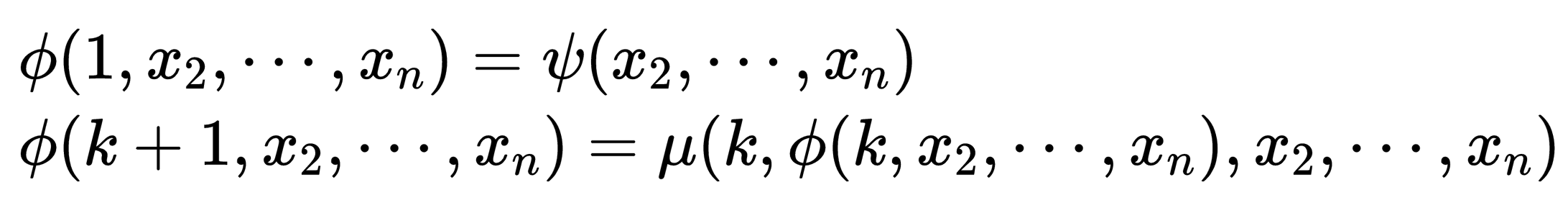
原始递归函数就是用上面的两种构造方法：代入和原始递归，从函数的初始储备所能作出的任意函数。

递归函数

如果想一下原始递归，而且知道一点可编程计算机的话，就会相信原始递归函数是有效的可计算的，就是说对于任何一个原始递归函数都有一个算法来计算它（例如原始递归运算通常都可以相当直接地作为一个FOR循环来实现。

逆定理是否成立？是否所有可计算函数都是原始递归的？例如考虑这样一个函数，它把正整数n映为p_n（即第n个素数）。不难做出一个简单的算法来计算p_n，然后这就是一个好的练习：把这个算法变成此函数为原始递归的证明（如果想了解什么是原始递归的话）。

然而，结果表明，这个函数是不典型的，有不是原始递归的可计算函数存在。 1928年，阿克尔曼就定义了一个函数，现在就叫做阿克尔曼函数，它有一个"双归纳"定义。下面的函数和阿克尔曼函数不完全相同，但是非常相似。这个函数A（c，y）是由下面的递推规则决定的：

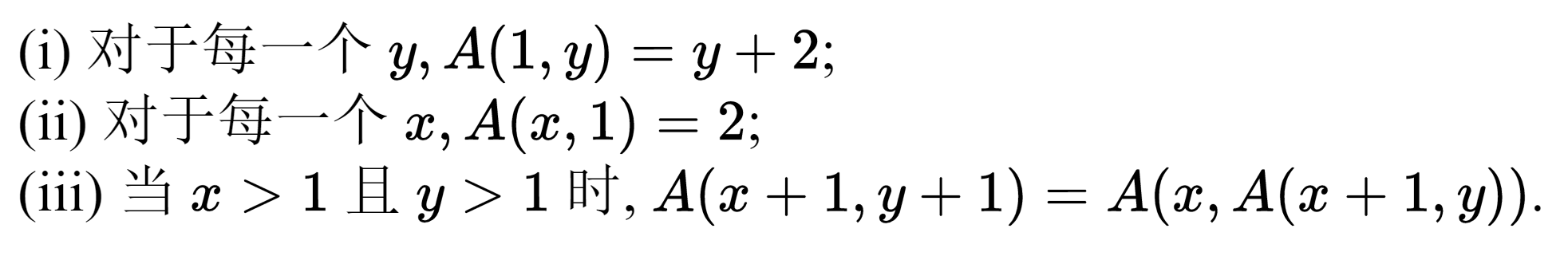
例如，

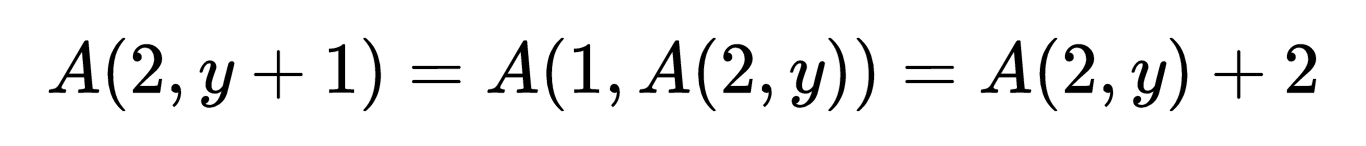
由此并由 A（2，1）=2这一事实可知，对于每一个y都有A（2，y）=2y。类似地可以证明，A（3，y）=2^y，而一般说来A（x＋1，y）将把函数y→A（x，y）"迭代"。这意味着，即使x和y相当小，A（x，y）也可能极大。例如，

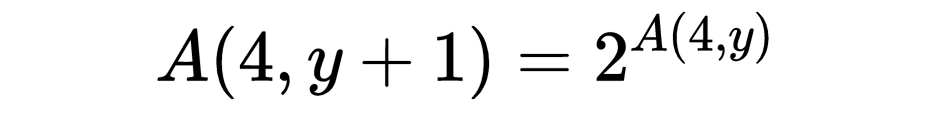
所以A（4，y）将有一个高为y的“指数塔”来表示，有 A（4，1），A（4，2）=2^2=4，A（4，3）=2^4=16，A（4，4）=2^16=65536，而到了A（4，5）=2^65536，就大得无法在这里用十进制来表示了。

可以证明，对于每一个原始递归函数ϕ，都有一个x，使得A（x，y）增长得比ϕ（y）更快，这一点可以用归纳论证来证明。略微简单化一点，如果已经证明了ψ（y）和μ（x）已经增长得比A（c，y）慢，则由原始递归生成的函数也增长得更慢。这样就可以定义一个"对角线函数"A（y）=A（y，y），它不是一个原始递归函数，因为它增长得比任意的A（x，y）都更快。

如果想准确地理解哪些函数是算法地可计算的，则我们的定义必须包括如阿克尔曼函数这样的函数，因为它们在原则上是可计算的。所以，必须考虑比原始递归函数更大的函数类。哥德尔、丘奇和克林各以不同方式做了这件事，而得到了同样的递归函数类。例如，克林就增加了第三个他称为极小化的构造方法：设f 是一个（n＋1）元函数，可以定义一个 n 元函数g 如下：g（x_1，……，x_n）就是满足f（x_1，…，x_n，y）=0的最小的y（如果没有这样的y存在，就说g对这个（x_1，…，x_n）没有定义。

结果就是，不仅阿克尔曼函数是递归函数，而且所有可以写出一个计算机程序类似计算的函数都是递归函数。这就给出了可计算性的形式定义，而这是以前没有的。

有效可计算性

当递归函数的概念得到陈述以后，丘奇就宣称递归函数类就是"有效可计算"的函数类。这项宣布得到了广泛的相信，但是是无法证明的。因为递归函数概念是一个精确的数学概念，而一个有效可计算函数只是一个直观的概念，很像"算法"概念那样。丘奇的宣布属于元数学的领域，现在通常被称为丘奇论题。

丘奇论题的最强有力的证据是：图灵在1938年找到了把算法概念形式化的一种看起来完全不同但图灵证明了是等价的一种表述，那就是在他的新意义下可计算的函数都是递归函数，其逆亦真。他的途径是：定义一个概念，现在称为图灵机，它可以看作一个极原始的计算机，而在后来实际的计算机发展中起了重要的作用。实际上，可以在图灵机上计算的函数恰好就是在真正的计算机上可以编程计算的函数。图灵机的原始结构，并不使它不那么强有力。因为递归函数就是图灵可计算函数，所以递归函数也就是可以在真实的计算机上编程计算的函数。所以，不相信丘奇论题就相当于坚持有不能转变为计算机程序的“有效程序”，而这是不可能的。

图灵引入图灵机是为了回应希尔伯特第十问题的一个推广：判定问题（decision problem）。这个问题也是希尔伯特提出的。他想要知道是否存在一种“机械的程序”，使得可以用来决定一个给定的数学命题能否证明。图灵为了考虑这个问题，需要对何谓“机械的程序”有一个精确的定义。一旦有了图灵机这个概念以后，他就能用一个相当直接的对角线论据证明对于希尔伯特的这个问题的答案为否。