2016年3月，Deepmind的AlphaGo以4比1的比分战胜18届围棋世界冠军李世石，这场比赛吸引到全球超过2亿观众。机器学会围棋策略，并击败人类顶尖高手，这在以往被视为一种不可能的壮举——或者至少被认为要到十年后才有可能实现。

AlphaGo对李世石第三盘比赛

这本身已经成就了历史性时刻。但2017年10月18日，DeepMind又再次迈出新的一大步。

在《无需人类知识掌握围棋游戏》论文当中，DeepMind公布了一种新的算法变种，即AlphaGo Zero——其能够以100比0的比分狂虐AlphaGo。令人难以置信的是，AlphaGo Zero完全通过自学掌握了围棋技艺，即以“白板”状态起步通过战胜自我进行学习。如此一来，无需人类围棋专家提供的数据库，超人类AI即可成为现实。

仅仅48天之后，DeepMind于2017年12月5日发布了另一篇题为《通过自我强化学习算法掌握国际象棋与将棋》的论文，展示了AlphaGo Zero如何在国际象棋与将棋领域分别击败最强程序StockFish与Elmo。更可怕的是，其整个学习过程是——从一窍不通到成为世界上最强的下棋程序——仅用了24个小时。

凭借如此恐怖的实力，AlphaZero正式诞生——这种通用型算法能够在无需人类专家策略作为知识基础的前提下，快速建立起适用于特定目标的一般性解决方法。

这样的能力无论如何夸大都不为过。这意味着AlphaGo Zero的底层方法能够利用完美信息（即比赛双方皆可随时了解全盘信息）适应任何游戏，即除游戏规则之外不再需要任何预先提供的专业指导。

也正因为如此，DeepMind才能够在初始AlphaGo Zero论文发布的短短48天之后，发布国际象棋与将棋版本。毫不夸张地讲，我们需要做的仅仅是变换用于描述游戏机制的输入文件，同时调整与神经网络以及蒙特卡洛树搜索相关的超参数。

如果说AlphaZero所使用的超复杂算法全世界只有少数人能够理解，仍然不会影响到这项卓越的成就。而更难能可贵的是，其核心实际上相当简单，甚至可以总结成以下几句概括：

通过潜在的未来场景设计游戏思维，优先考虑更具前景的途径，同时考虑对方可能选择的反应行为，同时继续探索未知。

在达成某种陌生状态后，评估对当前优势位置的信心，并将评分与此前采取的达成当前状态的思维途径进行映射。

在完成对未来可能性的思考之后，采取探索程度最高的行动。

在游戏结束时，返回并评估一切错误的未来位置价值评估，并相应更新自身理解。

这听起来正是我们每个人游玩游戏时的学习过程，对吧？当做出错误判断时，很可能是由于我们未能准确把握所占据位置的未来价值，或者错误判断了对手执行某种操作的可能性，因此错过了抢占先机的机会。而这些，正是成就 Alpha Zero游戏学习训练的两大根基。

在今天的文章中，我将尝试探讨以下三项内容：

1、AlphaZero之所以标志着人工智能发展一大步的两个理由。

2、如何重现AlphaZero方法以掌握Connect4游戏。

3、如何调整代码以适应其它游戏。

首先，查看AlphaGo Zero备忘清单以深入理解AlphaGo Zero的工作原理。我们显然有必要对代码中的各个组成部分进行遍历。

克隆此Git库，其中包含我所引用的代码。

要开始整个学习过程，首先请运行run.ipyng Jupyter记事本中的前两面。在建立起足够的游戏位置以填充自身记忆之后，神经网络即可开始训练。通过更多自我对抗及训练，其将能够慢慢提升游戏价值以及后续潜在位置移动判断方面的能力，从而做出更好的决策并获得更强大的游戏水平。

现在我们将查看具体代码内容，并展示一些结果，用以证明AI确实随着时间推移而变得愈发强大。

备注——这只是我个人对于AlphaZero工作原理的理解，这些理解主要基于前文提到的论文内容。如果以下存在任何谬误，我向大家诚挚道歉，并期待您能够加以纠正！

在本示例中，我们的算法将要学习如何进行Connect4游戏（或者叫四连棋）。其复杂程度当然无法与围棋相提并论……但其中仍然包含总计4531985219092个游戏位置。

游戏规则非常简单。玩家轮流在可用位置上放入自己颜色的棋子，第一个将四个己方棋子连成一排的玩家获胜——垂直、水平或者斜向皆可。如果整个棋盘都被填满但仍未出现四连一排，则游戏打成平局。

下面来看构成代码库的关键文件摘要：

game.py

此文件包含Connect4游戏的基本规则。

每个方格被分配一个数字，范围为由0到41，如下所示：

Connect4行动方块

Game.py文件提供游戏状态间的转移逻辑，并给出可选行动范围。举例来说，若当前为空棋盘且将棋子放在38号位，则takeAction方法会返回一个新的游戏状态，且起手玩家位于中央列的底部。

您可以利用任何拥有同样API的游戏文件替换game.py，算法会自动根据您提供的规则进行自我学习并逐步掌握游戏策略。

run.ipynb

本文件中包含开始学习过程的相关代码。其会加载游戏规则，而后通过主算法循环进行迭代，具体分为以下三个阶段：

1.  自我对抗

2.  重新训练神经网络

3.  评估神经网络

此循环当中主要涉及两个代理，分别为best_player与current_player。

其中best_player包含表现最好 神经网络，并将被用于生成自我对抗记忆。而current_player随后会根据记忆重新训练其神经网络，而后做出最好的选择。如果赢了，那么best_player当中的神经网络会被切换为current_player中的神经网络，而后再次开始循环。

agent.py

此文件当中包含Agent类（游戏中的一位玩家）。每个玩家都会利用自己的神经网络与蒙特卡洛树进行初始化。

其中simulate方法运行蒙特卡洛树搜索过程。具体来讲，该代理移动至对的叶节点，利用其神经网络评估该节点，而后通过该树回填该节点的值。

而act方法则多次重复模拟，从而理解当前哪个位置为最优行动。此后，其会将选定的行动返回给游戏，并实际加以执行。

最后是replay方法，其负责利用原有游戏记忆对神经网络进行重新训练。

此文件包含Residual_CNN类，其负责定义如何构建神经网络实例。

它利用AlphaGo Zero论文当中提到的一种神经网络架构缩写形式——即卷积层，而后为大量剩余层，最终拆分为一个值与策略标头。

各卷积过滤器的深度与数量可以在配置文件当中指定。

Keras库负责构建该网络，后端则由TensorFlow充当。

要查看该神经网络当中的各独立卷积过滤器以及密集连接层，请在run.ipyng记事本当中运行以下命令：

current_player.model.viewLayers()

神经网络中的卷积过滤器

其中包含Node、Edge与MCTS类，其共同构成蒙特卡洛搜索树。

MCTS类包含之前提到的moveToLeaf与backFill方法，且Edge类的各实例存储与每项潜在移动相关的统计信息。

config.py

在此文件中，大家可以设置将对算法造成影响的关键参数。

调整上述变量会对运行时间、神经网络准确性以及算法的整体成功率造成影响。上述参数能够产生高质量Connect4玩家，但需要很长时间才能学习完成。要加快算法速度，请尝试使用以下参数。

此文件当中包含 playMatches与playMatchesBetweenVersions函数，负责实现两个代理间的对抗。

要进行自我对抗，请运行以下代码（同样位于run.ipynb记事本当中）：

from game importGame

from funcs importplayMatchesBetweenVersions

importloggers as lg

env = Game()

playMatchesBetweenVersions(

env

, 1 #计算机玩家所在的运行版本号

, -1 #第一玩家版本号（-1为人类）

, 12 #第二玩家的版本号（-1为人类）

, 10 #进行多少盘游戏

, lg.logger_tourney #游戏日志记录位置

, 0 #哪个玩家先起手，-0为随机

)

在运行算法时，所有模型与记忆文件都将被保存在root目录下的run文件夹内。

若需要稍后从此检查点重新启动算法，请将run文件夹移动至run_archive文件夹，并在文件夹名称中添加运行编号。接下来，在initialise.py文件中输入运行编号、模型版本号以及记忆版本号，对应于run_archive文件夹中相关文件的位置。这样如往常一样运行算法后，即可从此检查点开始。

Memory类的一个实例，用于存储以往游戏的记忆，以供算法对current_pkayer神经网络进行重新训练。

此文件中包含一项自定义丢失函数，其会在将预测结果发送至交叉熵丢失函数之前地其进行模糊，从而避免出现非法移动。

Run与run_archive文件夹的位置。

日志文件被保存在run文件夹当中的log文件夹内。

要启动日志记录，请在文件中将logger_disabled变量的值设置为False。

查看日志文件将帮助我们理解算法的工作状态并掌握其“思路”。举例来说，以下为logger.mcts文件样本。

来自logger.mcts文件的输出结果

在logger.tourney当中，您可以看到评估阶段当中每项移动的具体可能性：

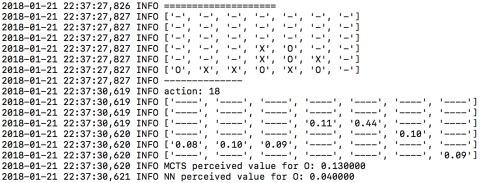
来自logger.tourney文件的输出结果

通过几天的训练，以下为小批量迭代后产生的图表：

小批量迭代中的丢失情况

第一行为策略标头中的误差（MCTS移动可能性中的交叉熵，针对来自神经网络的输出结果）。最下一行则为值标头（实际游戏价值与神经网络预测值之间的均方误差）误差。中间一行则为二者的平均值。

很明显，该神经网络在预测每种游戏状态值以及潜在下一动移动方面表现得越来越好。为了显示这一结果的提升过程，我从第1次迭代到第49次迭代当中选出17个玩家组成联盟。每个玩家进行两次配对，并在其中获得一次起手权。

以下为最终排名：

很明显，该神经网络的新版本要比初始版本更胜一筹，赢得了大部分游戏。另外，学习似乎还没有饱和——随着训练时间的进一步延长，其游戏水平变得更为强大，并能够学习到愈发复杂的策略。

举例来说，神经网络在学习过程中发现的第一项明确策略在于尽早抢占中央列。观察该算法最初版本与第30次迭代版本间的差异，会发现：

神经网络最初版本

神经网络第30次迭代版本

这是一项很好的策略，因为大多四连排布都需要经过中间列——因此应尽早阻止对手利用这一点。神经网络在无需任何人为输入的前提下发现了这项规律。

项目的games文件夹当中有一个面向“Metasquares”游戏的game.py文件，其基本规则是在网格当中画下X与O，从而尽可能形成不同大小的正方形。正方形面积越大，得分则越高。当网格被画满时，得分最高的玩家获胜。

如果你将Connect4 game.py文件切换为Metasquares game.py文件，即可通过同样的算法学习如何玩转Metasquares游戏。

来源：medium.com

作者：David Foster

编译整理：科技行者