我们时常会遇到一些计算规则，它们在定义一个序列的元素时，要用到序列中在它前面的元素。这时就有两种不同的进行计算的办法。第一个办法是迭代，就是先算出第一个元素，再用递推公式算出下面的元素。第二个办法是递归，这个办法初看起来是循环的，因为在定义一个过程时，用到了过程本身。让我们用一些例子来说明递归与迭代的区别。

设我们想要计算 n！=1·2·3…（n-1）·n。显然，这里有一个递推关系：n！=n·（n-1）！，还有初始值1！=1。做完了第一步以后，就能相继地算出 2！，3！，4！等等，一直到算出 n！为止。另一个办法是：把计算阶乘作为一个程序，记作FACT，而用FACT（n）表示执行这个程序到n！的结果，于是FACT（n）=n×FACT（n-1），这就是一个递归程序。

第二个办法是：为了知道如何得到n！，只需知道如何得到（n-1）！，而为了知道如何得到（n-1）！，只需知道如何得到（n-2）！，以此类推。因为1！=1，所以能得到n！。这样，递归有点像是把迭代“倒过来”考虑。

从某些方面来说，用这个例子来说明这两种程序的差别是太简单了。此外，如果真要计算 n！，则迭代比递归更加简单和自然。现在我们再看一个例子，这里递归就比迭代简单得多了。

梵天塔

梵天塔是卢卡斯（法国数学家）发明的一种数学游戏，设有n个圆盘，大小不一，盘的中心是一个小洞，按大小把它们叠在一根小柱A上。大的放在下面。还有另外两根空柱子B和C。问题是如何把原来在柱子A上的一摞圆盘移到柱子B，但要服从以下规则：每次只许移动一个圆盘，每一次都只能移动一根柱子最上面的圆盘放到另一根柱子上，此外任何时刻都不许把圆盘压在较小的圆盘上。

如果只有3个圆盘，这个问题是很容易的，但是当圆盘数目增加时，难度就快速增加了。然而借助于递归，就能很快地找到按照要求移动圆盘的算法了。 事实上，假设我们已经知道移动n-1个圆盘的程序H（n-1），则下面就是移动n个圆盘的程序 H（n）：先把小柱 A上的上面n-1个圆盘用程序H（n-1）移到小柱C上，再把A上的最后一个移到B上；最后再用H（n-1）把C上的n-1个圆盘全部按规则移到 B 上，而问题完全解决。我们可以把这个递归程序用符号写为

很容易用归纳法得出，整个程序包含2^n - 1步，此外，还能得知，这个任务不可能以更少的步数来完成。所以步数必为n的指数函数，而对于大的n。这个程序是很长的。

更进一步说，n越大，就需要更多的存贮单元来追踪我们的程序已经进行到哪一步了。与此相对照的是，如果我们想在迭代程序中实行一次迭代，我们只需要知道上一步迭代的结果就够了。所以，我们最需要记忆的只是一次迭代的结果。对于梵天塔，确实也有一个迭代程序。描述这个程序很容易，但是，这个程序确实能解决问题，却不是那么明显。它把这n个圆盘的位置编码成为一个n位的序列，而在每一步都给出得到下一个 n 位序列的很简单的规则。这个规则并不参照程序已经执行了多少步，所以，除了用来存贮圆盘位置外，所需记忆的量是很小的。

推广的欧几里得算法

欧几里得算法又称辗转相除法，是指用于计算两个非负整数a，b的最大公约数。应用领域有数学和计算机两个方面。计算公式gcd(a,b) = gcd(b,a mod b)。

欧几里得算法是很容易可以自然化为递归的另一个例子。如果a和b是两个正整数，则可以写出a=qb＋r，0≤r<b。这个算法依据的是下面的观察：gcd（a，b）=gcd（b，r）。因为余数r很容易从a和b算出，又因为数对（b，r）小于数对（a，b），所以，这就给了一个递归程序，而在遇到（a，0）形式的数对时就会停止。

欧几里得算法的一个重要推广是贝祖引理。这个引理指出，对于任意一对正整数 a 和 b，一定存在一对整数（不一定都为正）u和v，使得

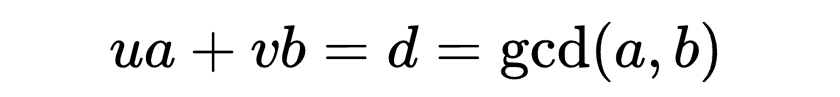
怎样去求这种整数u，v呢？推广的欧几里得算法给出了答案，而它又是可以由递归来定义的。设对于b和r，能够找到一对（u'，v'）使得

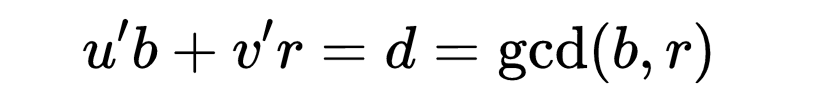
则因a=bg＋r，可以把r=a-qb代入上式，而得

这样，若令u=v'，v=u'-v'q，就得到了d=ua＋ub。因为对于a和b所需的数对（u，n）可以容易地从较小的b和r所需的（u'，v'）算出。这就给了一个递归程序。r=0就是递归的"底"，这样就有1b＋0r=d。一旦到了这时，就可以“往回走”，通过欧几里得算法，按照上面的规则逐步修改（u，v）。

迄今我们都是作为理论来讨论算法，而忽略了它的实用性。然而，单是有算法存在，还不一定能保证计算机能够执行它，因为有些算法包含的步数如此之多，使得没有一种计算机能够执行。一种算法的复杂性，粗略地说，就是它完成一项任务所需的步数。更准确地说，这是算法的时间复杂性。还有空间复杂性，是指为了执行这个任务所需的存贮的多少。复杂性理论研究的就是完成各种任务所需的计算机资源。

欧几里得算法的复杂性

计算机执行欧几里得算法所需的时间与计算商和余数所需的时间密切相关，也就是与递归程序访问其自身的次数密切相关。当然，这个数进一步又依赖于想要求其 gcd 的数 a和b的大小。一个初始的观察是：如果 0<b≤ a，则 a 除以 b 的余数必小于a/2。由此可知，在求余数时，只要计算了两步，就可以得到一个数对，而其第一个分量最多只有原来的第一个分量的一半，由此容易看到，计算余数最多只需要

而此数大体上与a的位数成正比。因为一个数的位数远小于此数本身，这个算法可以很容易地用于很大的数，这就使它除有理论意义外，还有很大的实用性。

所需除法的次数，在最坏的情况下是多少，这个问题直到19世纪上半叶才有人研究。上面给出的界限是由芬克在1841年得出的。但是不难看到，这个结果可以稍加改善，而证明当a和b是斐波那契数列的相继两项时，算法最长。这意味着所需除法的数目绝不会超过

欧几里得算法还有很低的空间复杂性。当把数对（a，b）代以数对（b，r）后，就可以忘掉原来的数对，所以在任何阶段都不必记住很多东西（也就是不必把它放在计算机的存贮内）。与此相对照，推广的欧几里得算法表面上看，需要记住导致 a 和b的gcd d的全部计算过程，因为这样就可以做一系列代入以得出u和v使得ya＋bu=d。但是仔细看一下，又可以看出，在任何时刻，只需记住少数几步就可以完成这个工作。

让我们用一个例子来说明这是怎么做的。我们设 a= 38，b= 21，很明显gcd（38，21）=1。现在要找出u和v使得38u＋21v=1。

我们从写出欧几里得算法的第一步开始：38=1×21＋17。这一步告诉我们17=38-21。

再作第二步：21=1×17＋4。我们已经知道了如何用38和21表示17，把它代入上式，就有21=1×(38-21)＋4。

移项以后可得4=2×21-38。现在再来作欧几里得算法的第三步：17=4×4＋1。

只要记住第一步和第二步的结果，就可以把17和4都用38和21表示，所以再代入一次就有38-21=4×(2×21-38)＋1。

整理以后就有1=5×38-9×21，而问题完全解决。

可见只需记住两步的结果。

想一想这个过程就会看到，在每一阶段都只需要记住某两个数（例如上面的17 和 4）是怎样用 a 和b 表示的。所以推广的欧几里得算法，如果适当执行，其空间复杂性也是很小的。