在数学（和大多数理论物理）中，狄拉克delta函数是一个实数上的广义函数。它的值除了在x=0处，都是0，并且从无穷处开始的积分等于1。

狄拉克delta函数由保罗·狄拉克提出，它的图形（几乎）就是整个x轴和正y轴。对于每一个非零x的值，函数的值都是0。但在0处，函数值是无穷大的。

这是一个很奇怪的图，函数只在0处出现峰值，对于任何其他的x值，不管它有多接近于零，函数总是零。

这里有很多复杂的数学问题。你可能会想问“这是一个数学函数吗？”，“我们如何处理一个不会持续变化的函数？”。我不会在这里讲太多细节。

在我们深入研究它的物理性质之前，关于函数的另一个值得注意的性质是它的积分正好是1。对于任何一般的函数，我们求积分就是求曲线下的面积。

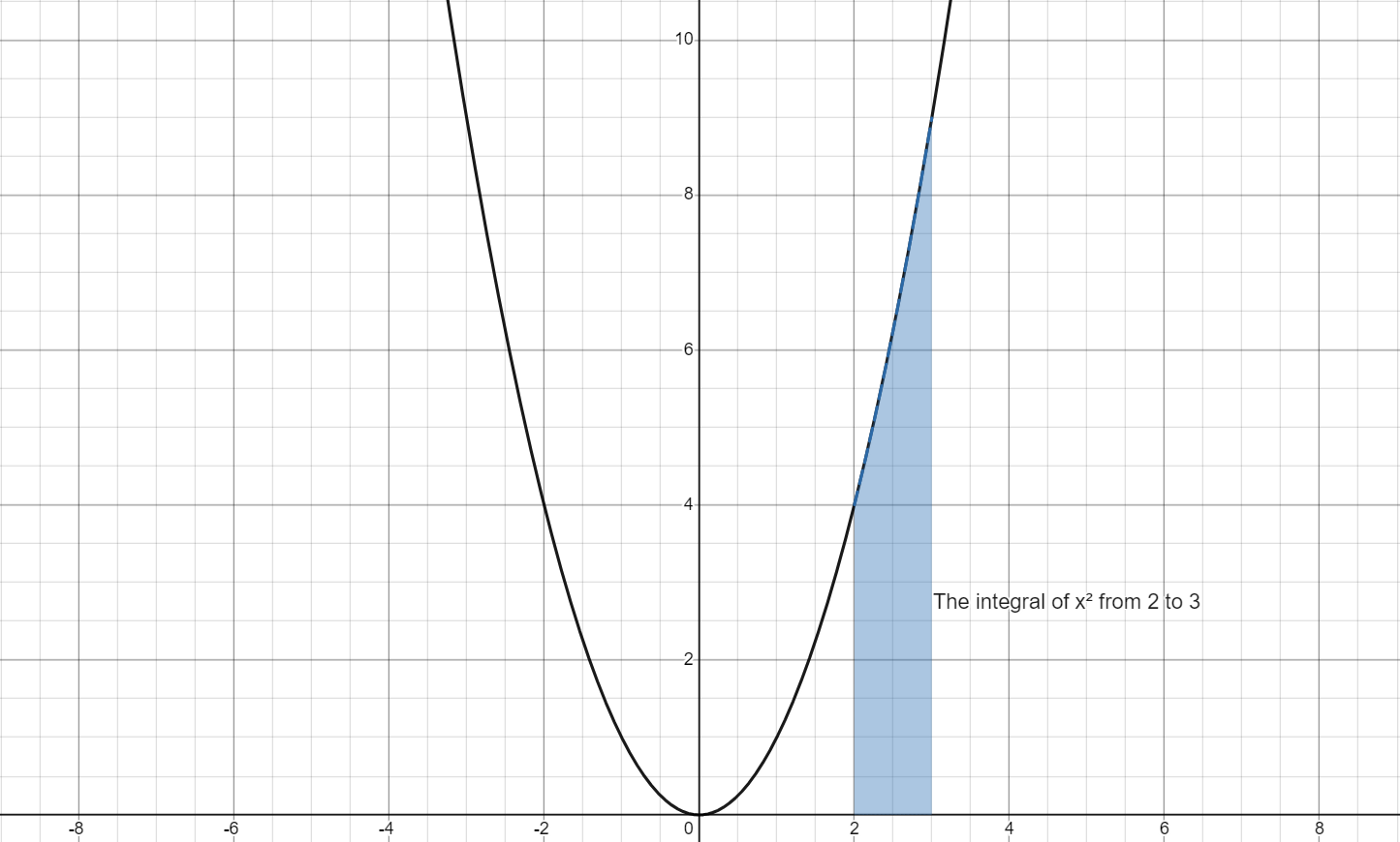
从2到3求积分得到蓝色阴影部分的面积

这个积分的数学公式

积分的意思是，这个面积在几何上不容易求出来。我们转而求助于数学公式。这和把曲线下的面积分割成无穷多个矩形并把它们的面积加起来是一样的。

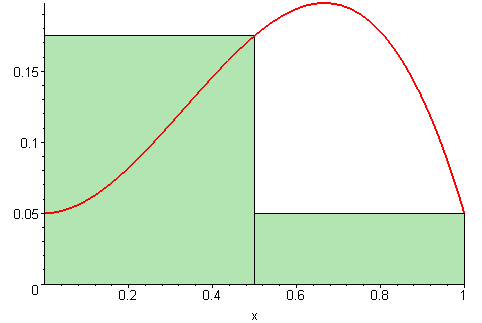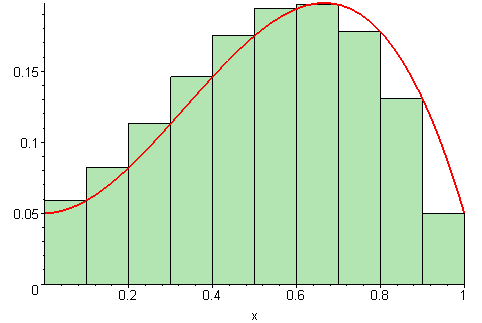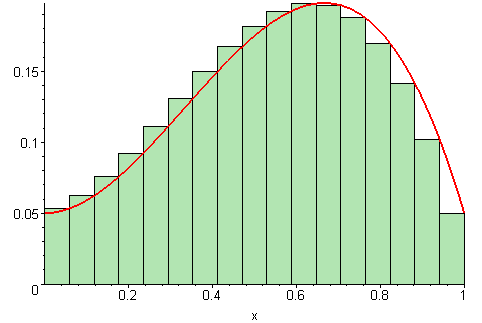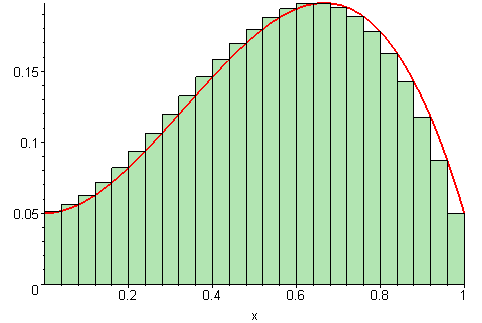
delta函数有特殊的定义，使得它的积分等于1。在整个空间中，你会发现由函数和x轴限定的面积是1。

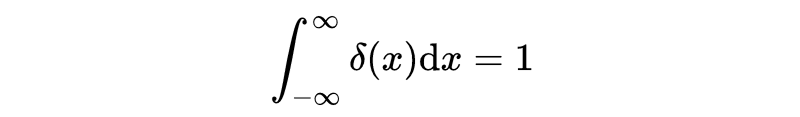
奇怪的是，这个函数的宽度是零，高度是无限的，但是这个函数下的面积是有限的：1。这只是狄拉克delta函数的一个性质。

此外，函数不一定要在x = 0处出现特别的尖峰。我们可以把这个函数（图）移动到我们想要的地方，只需从因变量x中减去某个值，比如说a，那么我们所做的实际上是将整个图形向右平移了a个单位。

我们也可以对delta函数做同样的处理。

这很重要的原因是，我们现在可以取另一个函数（比如说sin函数），然后乘以delta(x-a)，然后如果我们对它积分，就会得到函数sin(x)在x = a处的值。

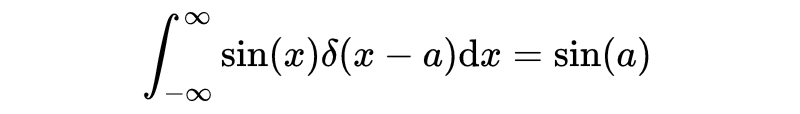
也就是说，delta函数可以用来“挑选”任何函数的值。但这就是数学的意义所在。

物理上的意义

还有一个非常重要的问题：“一个无限窄和无限高的函数如何帮助我们描述实数？”

尽管这种无限在我们的生活中没有出现，但理论物理中充满了这种无限。简单起见，我们经常把粒子当作质点。我们假设小粒子（如电子）的质量集中于一点。根据定义，点没有大小。

因此，我们经常把带电粒子当作“点”电荷。与考虑有限空间中电荷的分布相比，这使数学计算变得容易得多。但是狄拉克delta函数和这有什么关系呢？

数学上，这只是电荷对体积的导数。

重新整理这个公式来计算粒子的电荷，我们发现q仅仅是密度对体积的积分：

这和求导是相反的。两边同时乘以dV，然后对两边积分。现在，这个的物理解释是，粒子的电荷可以通过知道每一小块体积中有多少电荷来求得。我们得到电荷密度，然后用它乘以微小的体积，得到体积中微小的电荷。用文字来解释有点奇怪，所以我们用数学来代替，dq = ρdV。

我们把所有小的dqs加起来得到q。回想一下，对于一个质点，我们假设电荷完全不分散，它们都集中在一个点上，假设x = b。

简单起见，我们在一维系统中研究这个问题。具体来说，电荷密度等于定域在这一点的电荷乘以x-b的delta函数：

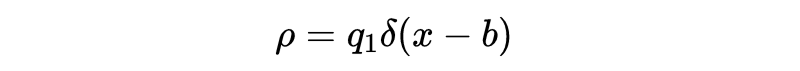
为什么这有效？把它带回我们的方程q是dV的积分，得到：

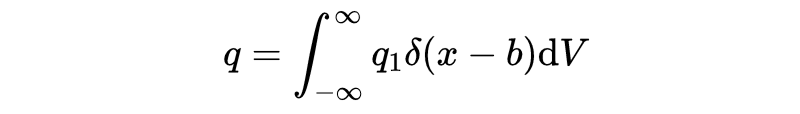
q1就是点电荷的大小。但这不太正确，因为我们忽略了y和z。之前我们说过，delta函数选取了另一个函数的值。在这种情况下，q1就是这个函数。数学上，q1就是一个常数函数。delta函数帮助我们在空间中带电粒子所在的点上找到它。需要强调的是，delta函数在现实生活中是不适用的（因为其无穷性）。而且电荷的分布也会散开，而不只是集中在空间中的一点。

只是当我们处理带电粒子时，它们与我们通常的测量单位相比是如此之小，以至于我们可以把粒子当作“没有大小的点”来处理。

狄拉克delta函数还不止于此。它可以用来求波函数在某一点的值。delta函数在量子力学中也很有用，粒子的波函数给出了“给定空间区域内”一个粒子的概率振幅。当狄拉克delta函数应用于波函数时，它会给出概率值。

然而，更重要的是，它也允许delta势的存在：一个由狄拉克delta函数在数学上很好地描述的势。这可以用来模拟粒子在两个空间区域中自由移动的情况（两个区域之间有屏障）。例如，电子可以在导电材料中几乎自由地移动，但如果两个导电表面紧密地放在一起，它们之间的界面作为电子的屏障，可以用delta势来近似。

狄拉克delta函数在物理上是不可能的，但在数学上却是必不可少的。