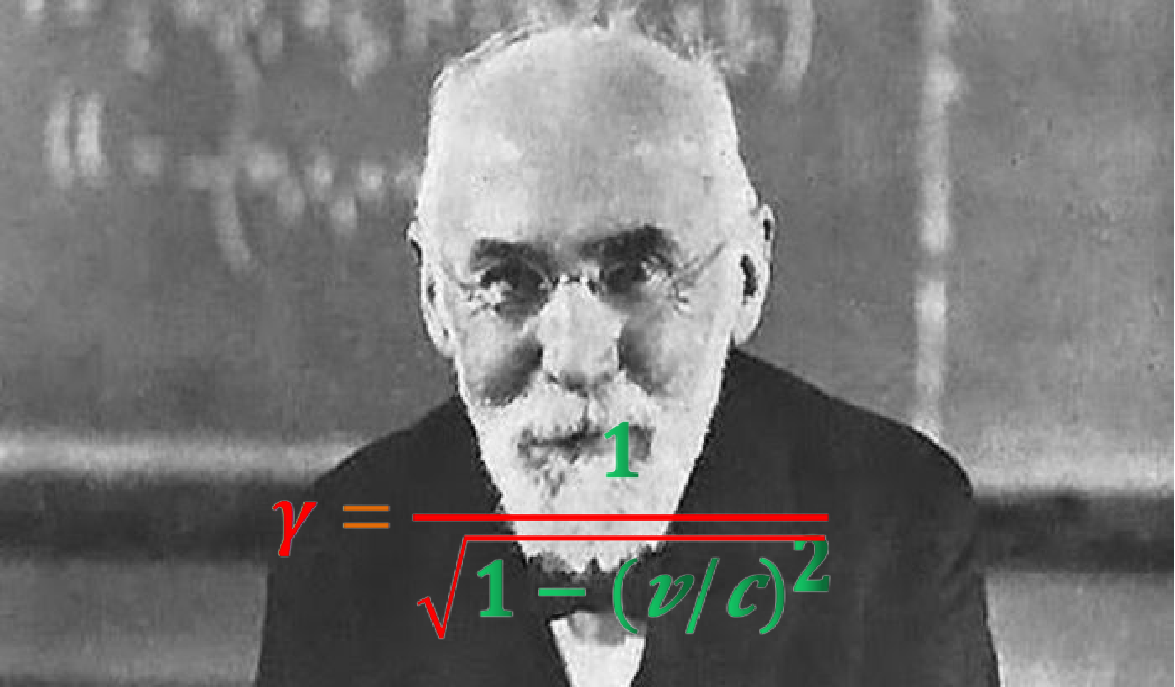
通过观察时空图从数学角度理解因果关系和狭义相对论中最重要的间隔不变性定理，我们已经对时空的奇特性质有了一些了解，我们需要发展出一个精确的代数公式，来说明不同惯性观测者的坐标如何变化。我们用一组叫作洛伦兹变换的方程来做这个，该方程首先由荷兰物理学家亨德里克·洛伦兹推导出来。

让我们重申一下我们正在做的事情的要点。事件t，x，y，z在时空中是由一个观测者用他的坐标系描述的。惯性系S'中的另一个观察者O'用他的坐标系描述了相同的事件t'， x'，y'，z'。基本的问题是：坐标t，x，y，z和t'，x'，y'，z'有什么关系？和往常一样，我们假设两个坐标系都是标准构型。

我们已经知道，如果第二个假设是正确的（光速c对所有惯性观测者来说都是恒定的），就不能用伽利略变换来比较一组坐标和另一组坐标。相反，我们使用洛伦兹变换。稍后我们将推导洛伦兹变换。现在我们只给他们表达式。

我们从洛伦兹因子开始，用希腊字母γ表示，其中：

ν是另两个坐标系统的相对速度，c是光速。从这个方程的结构中看出，如果ν大于等于c，就会出现零或负数的平方根，γ的表达式变得没有意义，这表明c是自然界中可能的最大速度。因此我们只考虑v小于c的情况。

现在我们看到，当ν≠0时，洛伦兹因子总是大于1。对于正常的日常速度，它会非常非常接近1，下图显示了洛伦兹因子随速度ν的变化情况：

洛伦兹因子作为速度的函数。

对于不同的ν/c值，洛伦兹因子的值如下：

ν/c

γ

0.000

1.000

0.100

1.005

0.300

1.048

0.500

1.155

0.700

1.400

0.900

2.294

0.990

7.089

0.999

22.366

洛伦兹因子代入洛伦兹变换，得到坐标t'，x' ，y'，z'的值。

洛伦兹变换是：

洛伦兹反变换（给出坐标t, x, y, z的值）是：

注意，当ν＜＜c时，洛伦兹变换近似于伽利略变换：

观察洛伦兹变换的一个有用的方法是，它允许我们在时空图上，校准第二坐标系的轴。

推导洛伦兹变换

我们现在可以推导洛伦兹变换。记住，我们试图找到事件在两个惯性系S和S’中的坐标之间的关系，S’以ν相对于S的速度运动。我们假设两个坐标系都是标准构型（所以我们可以忽略y和z坐标，而专注于t和x坐标）。

式1

牛顿第一定律适用于所有的惯性系，也就是说这些系统不能加速，因此我们省略平方项及更高次幂项，得到：

式2

现在我们需要找出未知常数：

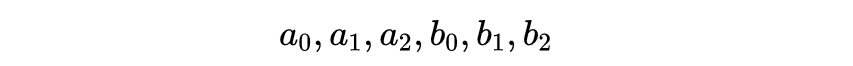
因为坐标系是标准构型，我们知道当原点与t' = t = 0和x' = x = 0重合时。因此它必须有：

我们现在可以说：

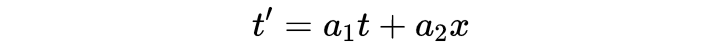
式3

式4

在时间t之后，坐标系S'（由x' = 0给出）的原点在坐标系S中移动了距离x = vt，因此我们可以将上式改写为：

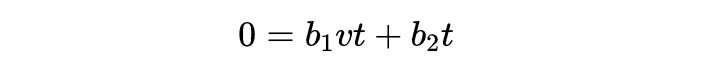
也就是：

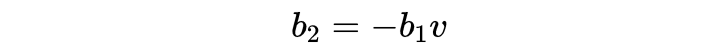
用式4除以式3，并把上式带入b_2得到：

式4

在时间t'之后，坐标系S（由x = 0给出）的原点在坐标系S'中的x' = -vt'处。因此可以将式4重写为：

得到a_1=b_1，带入式4得到：

式5

现在回想一下，狭义相对论的一个假设是，真空中的光速，在所有的惯性参照系中，都有相同的c值。这意味着，如果一束光从原点沿x轴正方向发射（ct = 0, x = 0），它的速度为c = x'/t'以及c = x/t，我们可以将其代入式7得到：

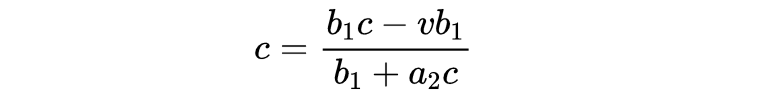
整理得：

因为a_1=b_1，所以有：

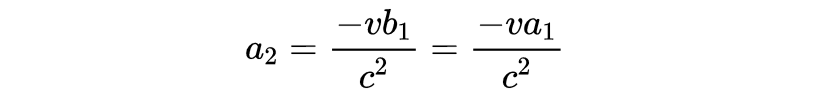
重写式3为：

式6

因此由式4，得到：

式7

现在我们需要用t和x表示式6和式7。实际上，这意味着我们已经从一个在坐标系S中的观察者改变了观察坐标系S'，成为坐标系S'的观察者，观察坐标系S，因此坐标系S沿着- x'轴远离我们，所以我们需要用-ν代替ν来得到：

式8

式9

我们快成功了。现在将式8和式9代入式7得到：

我们已经证明了这个常数a_1就是洛伦兹因子γ。

洛伦兹变换矩阵形式

洛伦兹变换的另一种表达方式是矩阵形式：

式10

右边的4 × 4矩阵叫做洛伦兹变换矩阵。

除以c得到：

也就是t'的洛伦兹变换。类似地，我们通过将右边两个矩阵相乘得到x' ，y'和z'。当我们讨论广义相对论中的向量和张量时我们会更详细地研究变换矩阵。用指数表示法，把洛伦兹变换矩阵写成更紧凑的形式：

式11

其中：

表示式10左侧的列向量，

是洛伦兹变换矩阵，

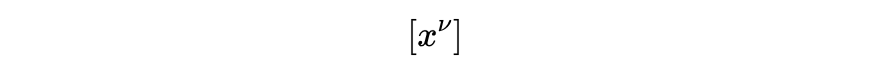
是式10右边的列向量，指数μ和ν取0到3的值，所以分量

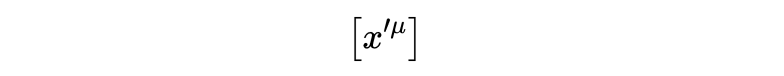
是：

分量

是：

变换矩阵的分量是：

其中μ指的是行，ν指的是列。

这个量：

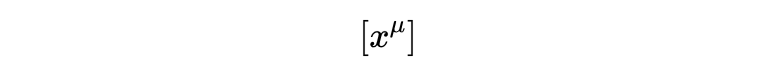
是“四位置”（我们第一个关于四矢量的例子），它用ct，x，y，z四个分量来描述时空中的事件或位置。

严格地说，式11中的方括号意味着我们引用的是矩阵。我们可以把这个方程写成矩阵的分量的形式：

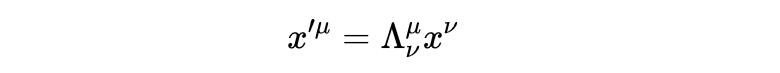
根据爱因斯坦求和约定，例如，μ=3时，那么

从现在开始，我们将经常使用这种简写的指数表示法。

第二个观察者

在上一篇文章中，我们利用光速c的恒常性在坐标系S'的时空图上构造第二个惯性坐标系S的坐标线ct'和x'。我们现在可以用洛伦兹变换用代数方法描述这些轴。

ct'的洛伦兹变换为：

式12

我们要求出x'轴的方程，也就是ct' = 0的直线。式12则为：

得到：

式13

也就是x'轴的方程。类似地，x'的洛伦兹变换是：

我们要求出ct'轴的方程，也就是x' = 0的直线。因此我们可以这样写：

得到：

乘以光速得：

式14

这是ct'轴的方程。

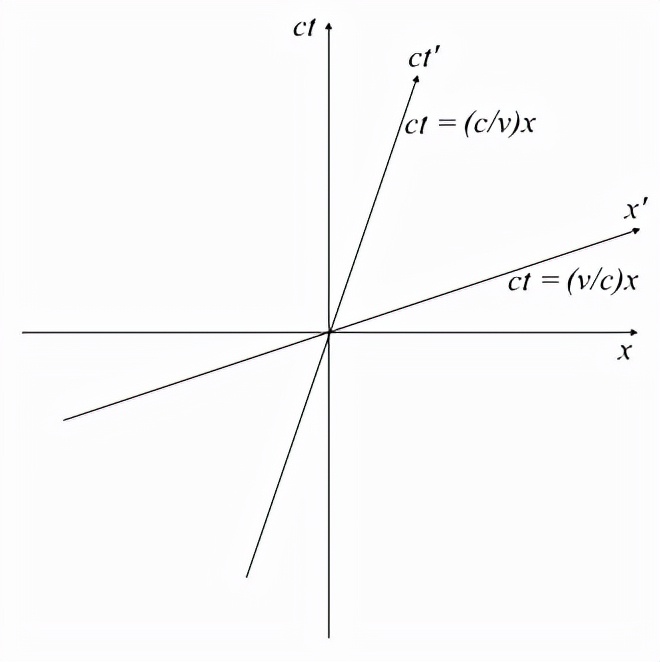
用洛伦兹变换求第二个观测者的坐标线。

间隔转换规则

洛伦兹变换告诉我们事件（即时空中的单点）是如何从一个坐标系转换到另一个坐标系的。如果在时空中有两个事件，那么相应的时间坐标和空间坐标之间就会有差异。正如我们已经注意到的，这些差异Δt， Δy，Δx，Δz称为间隔。

了解时空间隔是如何变换的是非常有必要的。我们推导出区间变换的规则如下。对于标记为1和2的两个事件，洛伦兹变换为：

式15

式16

如果我们能知道：

和

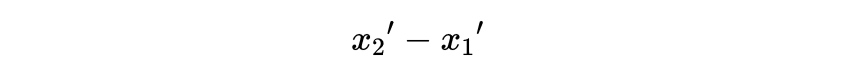
我们就知道了这些间隔的变换规则

式17

式18

其中：

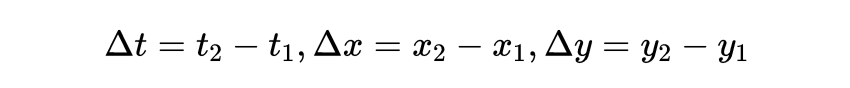
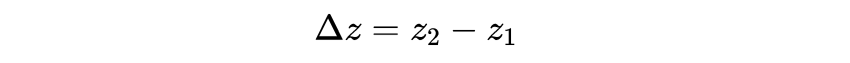
类似地，使用反洛仑兹变换，得到：

式19

式20

固有时和时间膨胀

在前面的文章，我们讨论不变双曲线的性质时，提到了时间膨胀的反直觉现象。现在我们用洛伦兹变换更仔细地观察时间膨胀。

到目前为止，我们一直使用的是坐标时间，坐标时间指的是一个遥远的观察者用自己的时钟测量的时间。正如我们所看到的，每个惯性系都有自己的时间坐标（时空图上不同的时间轴）。坐标时间因观测者的不同而不同。但是观察者用他们自己的时钟测量的时间呢？这是一个不变的时间度量，称为固有时，我们可以用它来计算时间膨胀。

在实验室系统S中运动的粒子

假设我们在一个实验室里研究亚原子粒子，它们在正x方向上以恒定速度ν运动。假设我们正在研究的粒子是短命的，它是在一个我们称之为事件1的时空点上产生的，然后在另一个标记为事件2的点上衰变。

我们是观察者O，如果，事件1和事件2发生，那么我们测量粒子的寿命：

粒子移动的距离是：

但是还有一个很明显的参考系需要考虑，那就是S'坐标系中的观察者O'，和粒子一起运动。这叫做粒子的静止坐标系。

你可以想象一下这样的场景，你正在驾驶一辆汽车，在你旁边的副驾驶座位上有一个购物袋。购物袋等价于粒子，你是观察者O'，而汽车是袋子的静止坐标系S'。站在路边的人们会看到购物袋以每小时70英里的速度从他们身边呼啸而过。但对你来说，这个袋子是固定的。

静止坐标系S'中的粒子

上图显示了静止坐标系S'下的粒子。就像购物袋相对于你是静止的，所以根据观察者O'，粒子在产生和衰变之间不会在空间上移动。

在狭义相对论中，固有时是观察者在其静止坐标系中测量的时间。固有时用希腊字母tau（τ）表示。在我们的例子中，我们可以想象一个精确的时钟绑在粒子上。这是难以想象的，所以考虑粒子的自然“内部时钟”可能会更容易，这种未知的机制最终会对粒子说，“恐怕时间到了。”内部时钟记录的时间是粒子的固有时间。

对于粒子，事件1和事件2之间的固有时为：

现在我们有两种测量粒子寿命的方法：（1）坐标时间：

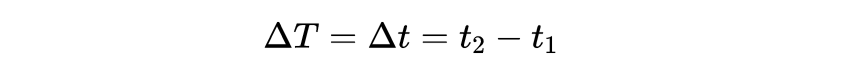
我们用实验室里的仪器进行测量，以及（2）固有时：

这是通过粒子自身的内部时钟来测量的。我们可以用间隔变换规则将两者联系起来：

因为：

所以：

另一种观察这个过程的方法是，一个过程需要一个特定的固有时，而另一个相对于静止坐标系运动的观察者所测量到的持续时间更长，即运动的时钟运行缓慢。这就是我们在上一篇文章中讨论的时间膨胀现象。

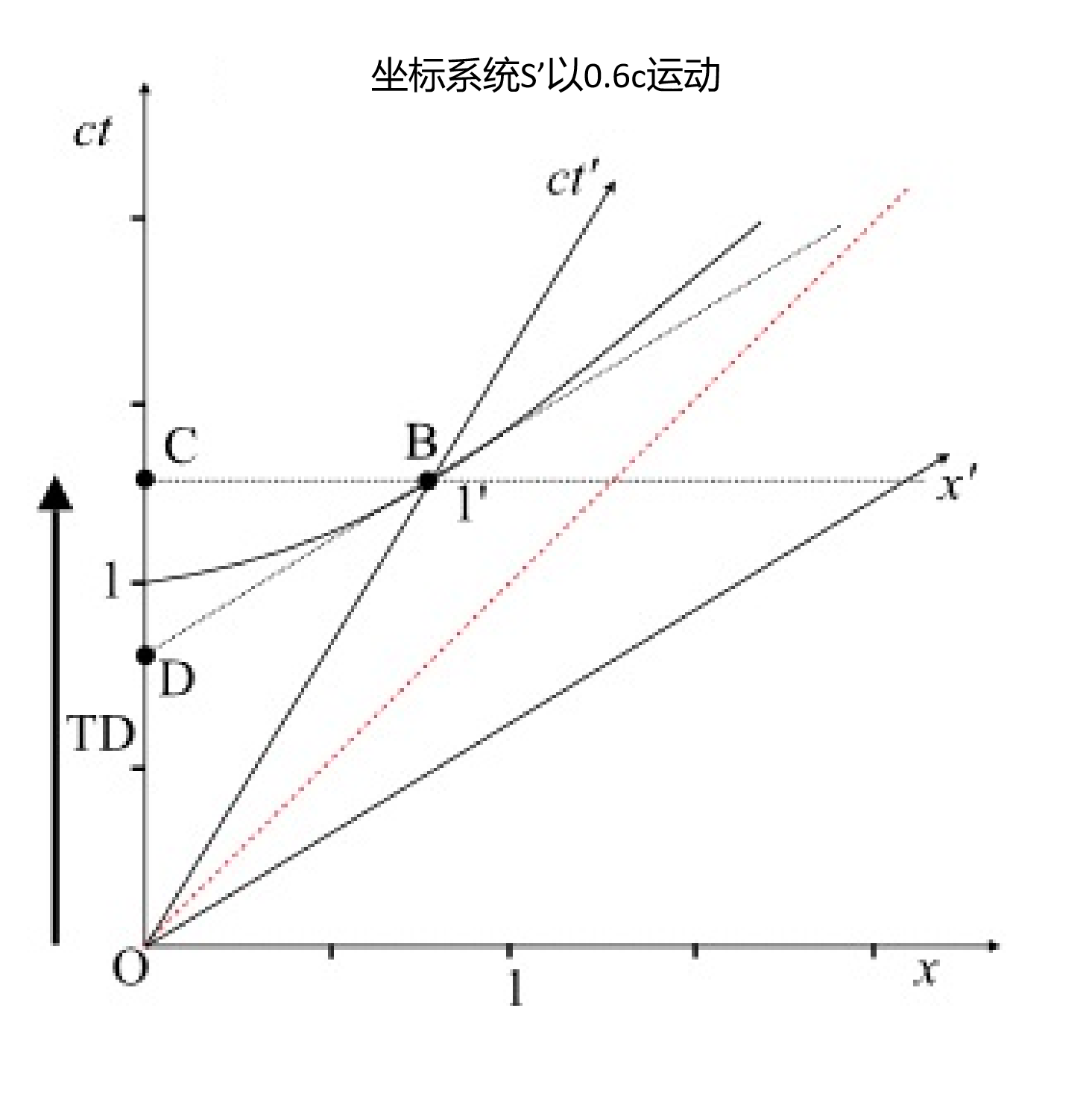
黑色箭头TD是由O'沿着ct'轴测量的B = 1事件的时间膨胀ΔT。我们如何计算黑箭头TD的长度？我们发现事件B的固有时由O'测得：

长度收缩

我们已经用时空图来探索长度收缩的现象。现在，我们更仔细地看看使用洛伦兹变换的长度收缩。

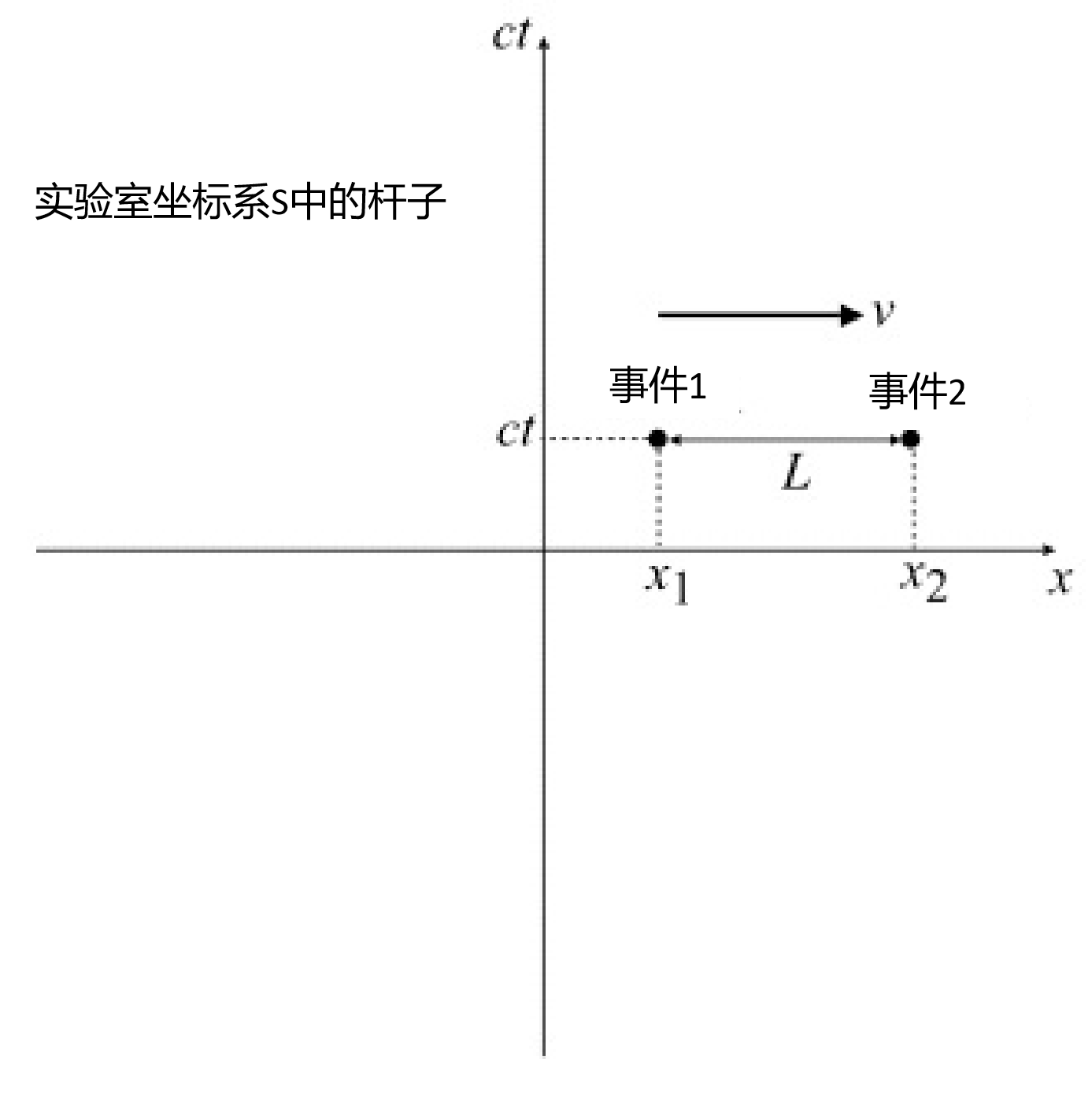
在实验室坐标系中的杆子（棒）

上图显示了在实验室惯性坐标系S下，杆以速度ν沿x轴纵向运动。杆的长度L可以通过假设杆的一端（对应于事件1）和另一端（对应于事件2）来测量。杆子的长度将为：

现在，就像我们对时间膨胀所做的那样，考虑杆处于静止坐标系S’中，杆沿x’轴静止，如上图所示。我们知道事件1和2仍然会发生在杆的末端，但我们不知道这些事件发生的时间。如果，在静止坐标系中，事件1和事件2分别发生，观察者O'将测量杆的长度（称为杆的固有长度）：

因为我们不知道

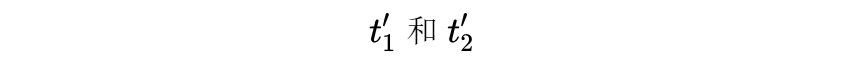
因此也不知道：

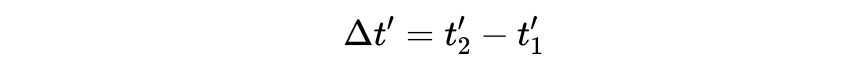
但这不是问题，因为我们可以使用间隔转换：

把表达式带入：

得到：

回忆一下，黑色箭头LC是由O观察到的长度收缩L，长度OD = 1由O'沿着x'轴测量。我们如何计算黑箭头LC的长度？

利用上式，其中L_p=1，得到：

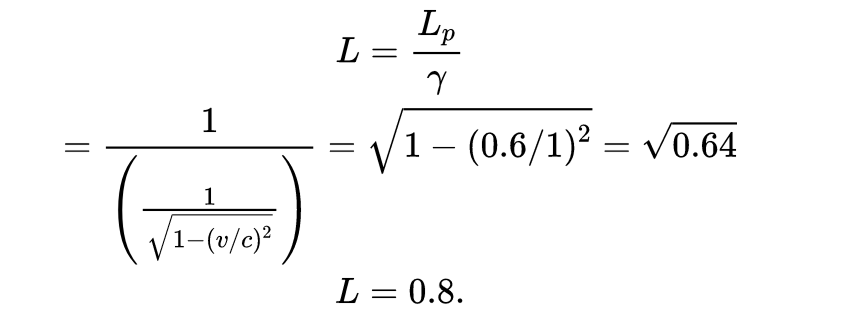
同时性的终结

我们在看时空图时发现，事件的同时性可以依赖于观察者的参照系。我们可以用间隔变换规则来进行代数表示

如果在坐标系S中两个事件同时发生，那么：

只要它们不发生在同一点，我们就可以说：

其中L为距离Δx。这个方程是同时性相对性的代数公式。我们可以看到，对于非常低的速度（v＜＜c），有：

速度变换

上图显示了标准构型的两个惯性系，一个物体沿坐标系S的x轴以速度v_x运动。根据坐标系S'中的观察者，物体的运动速度v'是多少？对于这例子，伽利略的答案将是：

现在我们用洛伦兹变换来解决这个问题。我们可以使用两个间隔转换规则：

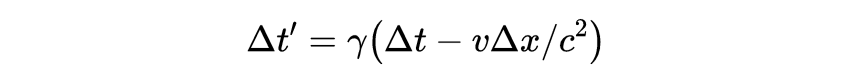
和

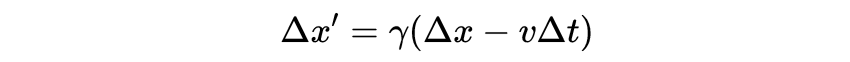
描述在坐标系S的x轴上发生的两个事件，如果我们用第二个方程除以第一个，得到：

接下来，我们将右边的顶部和底部表达式除以Δt：

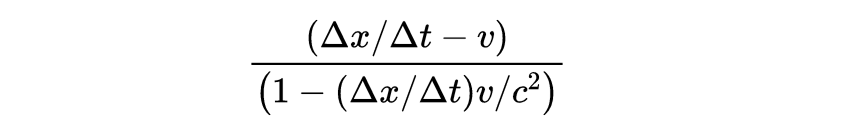
如果我们让x轴上的两个事件越来越近，最终，当Δx和Δt接近0时，得到这两个事件的瞬时速度。上式则为：

这个方程告诉我们什么？

首先，如果和v_x和v，与光速相比非常小，就会得到伽利略速度。其次，让我们考虑一下，如果物体现在是一束向坐标系S'相反方向移动的光线，会发生什么？在S'坐标系下，观测者测量光线的速度有多快？

狭义相对论的第二个假定指出，在所有惯性参照系中，光速在真空中的值c = 3 × 10^8 米每秒。根据第二个假设答案应该是-c。但是速度变换给了我们什么？

把v_x=-c带入速度变换（上式）方程中，得到：

整理得到：

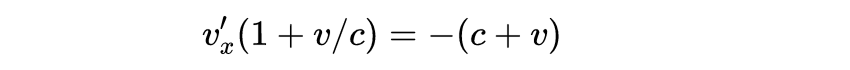
那么：

因此：

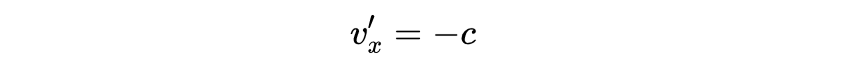
这正是第二个假设所要求的。正如预期的那样，我们也可以看到这与坐标系S和S'的相对运动无关。