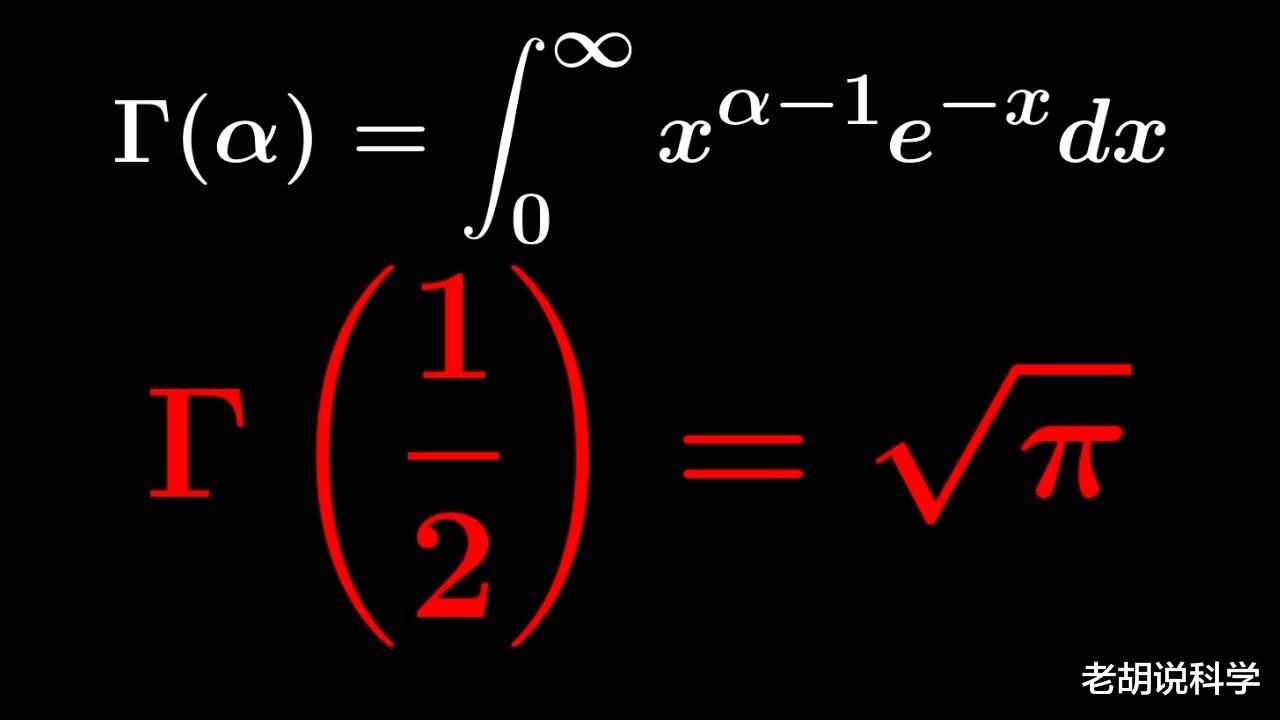
从阶乘的定义开始,我们可以在数学上证明:0!=1。在排列组合领域,通常给出的解释通常是,只有一种方法可以排列0个物体,或者数学家们发现了0!= 1而不是0!= 0更方便,更有用。
让我们先来看看什么是阶乘的定义。
一个非负整数n的阶乘,用n! 表示,是所有小于或等于n的正整数的积。
n!=(n)(n-1)(n-2)(n-3)…(3)(2)(1)
这就得到了一个递归关系。
n!=n (n-1)!
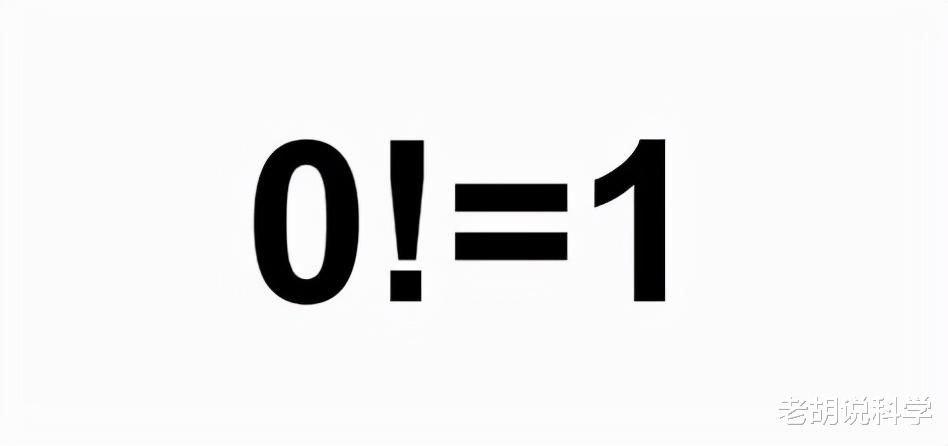
排列是一个集合中元素的唯一和特定的顺序。例如,包含三个元素的集合{a, b, c}有六种排列方式:
{a, b, c}, {a, c, b}, {b, c, a}, {b, a, c}, {c, b, a} 和 {c, a, b}。
从上面我们可以看出,3!=6。事实上,一个有四个元素的集合有4!=24个排列方式,一个有五个元素{a,b,c,d,e}的集合有5!=120个排列方式。因此,思考阶乘的另一种方式是设n是一个自然数,n!就是一个有n个元素的集合的排列数量。
以类似的方式,一个有两个元素的集合{a,b},有2!=2个排列组合,即{a,b}和{b,a}。有一个元素{a}的集合,有1!=1种排列组合,因为它只能以一种方式排序。
一个不包含任何元素的集合被称为空集。对于一个零元素的集合,可以有多少种排序方式?
我们已经知道,1!=1,2!=2,3!=6,4!=24,5!=120,……。现在让我们从后向前看,如何从5!=120中得到4!=24,以此类推。可以清楚地看到:
5!/5=24
4!/4=6
3!/3=2!
2!/2=1!
因此,0!=1!/1。从理论上讲,当n为有理数时,应该能够算出n阶乘的值。例如,什(3/2)!是多少?
伽马函数(gamma函数,γ函数)定义。设z是一个复数。伽马函数Γ(z)在ℜ(z)>0(半个复平面)中的定义为

这个积分在ℜ(z)>0时收敛。伽马函数的一个基本属性由以下命题给出:
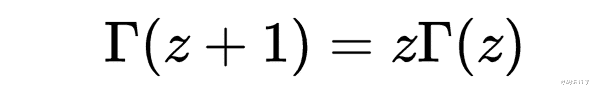
上述命题的证明非常简单,可以用分部积分法完成。
在1处对伽马函数进行求值,我们发现:

并使用上述命题,我们得到:

由此可见,对于所有正整数n:

伽马函数推广阶乘乘积的能力在数学的许多领域都有应用,例如,在组合学、概率论和幂级数的计算。

时光君
你把0当成一个数排列有一种排列方式,这应该解释为1的阶乘,0的阶乘为0,应当解释为什么都不存在的情况下,就是什么都不存在,拿什么排列!
时光君 回复 佛系东哥大战金铲铲 10-20 17:57
什么都没有你拿什么排列?按照你的说法,0个苹果有一个排列,0个香蕉有一个排列,0个苹果和0个香蕉一起有几个排列?
佛系东哥大战金铲铲 回复 10-20 17:45
什么都没有就只有一种排列
美国是双裁政权
哇,终于有人讨论老胡的文章了,说明绝大多数网友的文化水平是初中[呲牙笑]
DrCarter 回复 10-22 13:35
[点赞]一堆xxs讨论高数不解的样子,笑死
嗷嗷嗷
这会不会是因果导致,定义0!=1才推导出这个函数。你用这函数反向证明!
笑熬糨糊 回复 01-12 12:35
就是个定义而已。
3三叁
0.9....=1,别管为什么,人为定义的,记住就行
Hadden 回复 10-20 14:12
这个是可以通过极限定义证明的,不是人以定义的。0的阶乘值为1的确是人为规定的,当然这首先要保证它符合阶乘的运算规律——它的确符合(因为本来就是在确保它符合阶乘运算规律的情况下才定义的)。还有有理数的幂运算(乘方运算)也是这样推广到指数为0和负值的情况(除了0的0次方和负数次方):-2个2相乘有什么直观意义?没有,但直接按幂运算规则处理完全没问题,运算后结果为1/4即2个2相乘的倒数,那就规定有理数的负数次方结果是指数为原指数相反数的情况下计算出来的结果的倒数。后来发现在实数范围内这一结论都成立,那就把这一规则推广至实数范围。
逆鳞 回复 Hadden 10-22 16:59
那说明你没学好极限,极限只是无限趋近于一个地方
对方正在怼入
空集没得排列,0!=0[呲牙笑]
对方正在怼入 回复 用户15xxx12 10-21 16:30
就问你,空集有几个元素?没有元素也是一种元素是吧?也就是说空集有一个元素[得瑟],那一个元素的集合扔要哪里?
用户15xxx12 回复 10-20 18:45
数学中,无解也是一种解。这里也同理,什么也没有的排列方式只有一种,就是没有排列。
平凡
0!=1 是人为规定,为了表达式方便从零开始
天高云淡 回复 01-08 22:36
对的,就是规定,跟0是不是自然数一个道理,方便某些时候单独计算。,
用户10xxx65
0是个神奇的数字,一个0是0,两个0相加也是0,,一亿个0相加还是0,但无数个0相加却可以得任意数。如一个点的长度是0,但长度为3的线段是由无数个点构成的,所以无数个长度为0的点相加可以等于3。同理,无数个长度为0的点相加还可以得8,可以得任意数。
天翼you 回复 10-24 10:27
一旦出现荒唐一定是哪出现了问题,线段只能无限趋近但不会达到原点,所谓“线段由无数个点构成”中的“点”不是原点,它就是切割到粒子水平也是有尺度的,并非是你前面所说长度为零的点,此点非前点,你还是混肴了有限和无限的概念。
用户17xxx24 回复 10-27 22:11
但一个点的长度不是零啊,假如一个点的长度是零,我们就完犊子了[笑着哭]一维都成立不了
qzuser
虽然我不赞成小编的解释,但0!等于1是对的
追沙逐雪
阶乘要从1开始,因为阶乘代数式都是以1结束的零没有任何意义,零乘以任何数都是零。
开卷有益
证明0!=1应该就是回到阶乘定义本身,就像你已经写的(n-1)!×n=n!,取n=1,则有0!=1 。而你后面写的伽马函数,建立在用了阶乘这种简写形式的基础上,实际上是阶乘和伽马函数的综合应用,用这个证明不合理,但是应用于计算非整数阶乘是对的
maliang
這是否說明0和1在特定條件下是相等的,即0!=1!=1,所以,0=1。
用户74xxx89 回复 10-25 05:18
2²=(-2)²,难道2=-2?两个元素的映射结果相同不代表两个元素相同
思·易 回复 11-02 18:21
[得瑟]0=1=2
不是老路
还是表述为无意义更确切
不流命
一群弱智。0有阶乘吗?0乘以任何数等于0。
周莉 回复 12-18 16:32
你老娘来亲下厨
用户10xxx24 回复 周莉 12-21 07:47
哈哈哈
用户18xxx42
果然这种文章评论区最热闹,每一个小学初中文化的都能说两句[得瑟]
baboon
0都不在阶乘定义里面,还讨论什么!
哭了又笑就是你
这个初中考过,记住就好了 那个复平面的算法,也可以说是另一种算阶乘的定义吧。
不流命
阶乘是从1开始的,如果从零开始,任何数的阶乘都等于0。这么弱智的问题,为什么拿来忽悠人?要不要证明0+0=1?
无为
如果不定义0!=1,那么数学要打很多补丁
梓仪 回复 12-19 03:07
如果概念、定义不准确,应该打多少补钉,就得打多少补钉。不能省。[呲牙笑]
无为 回复 梓仪 12-19 12:06
于是,0!=1成为一个简便而又省事的补丁[吐舌头笑][吐舌头笑][吐舌头笑][吐舌头笑]
海龙王
Γ(3/2)=1/2Γ(1/2)=√π/2
鸿诚祥兆 焦军旭
一窍不通[笑着哭][笑着哭][笑着哭][笑着哭]
嗳回忆唯妳
小学数学,任何一个数乘以0结果都是0。0!=0 1!=1
用户10xxx65
3分之一乘以3
夏至360
你能证明出定义?跟本就是瞎扯淡。就像证明平行线为什么是平行的或不相交。
不流命
根据公式推导,一个数的阶乘等于它的绝对值的阶乘。所以负1的阶乘是1。负1难道没有阶乘吗?
5plus5
别去证明,只是规定而已。
周莉
1的阶乘等于1 所以0=1
super deal
我在B站看过小数阶乘算法,现在忘了2.5!怎么算
不流命 回复 11-18 13:53
[2.5]表示2.5的整数。正整数取整还是自己,正整数阶乘运算时,加入取整仍然成立,这样就可以使小数加入取整运算,然后进入阶乘运算。看来任何实数都可以进行阶乘运算。
Ysms 回复 11-25 22:26
2.5!的计算结果是出错的,但是不一定是无法表达的,比如说5/0,√-3
无为
乌龟的屁股!
鹰秀科技
这个无法证明。只能说是这么规定的。
用户32xxx50
我想知道这个作者是谁?这是环球的那个玩意么??
连杰12
好文分享一下你的时候
J.R Jeff
这个证明过程,有点。。。。
笑凌风
规定0!=1
海龙王
能否把0-2之间的函数绘在坐标上?让大家见识一下,特别是O-1之间有多少极值,最大值多少?
明夷
道生一
喵喵
Z能等于负1??
不流命
阶乘的推导公式运算和定义运算发生矛盾时,哪个为准?推导公式运算要是为准,我也可以弄个推导公式运算,n!=(|n|)!一个数的阶乘等于它的绝对值的阶乘。那么负整数也有阶乘。谁来证明负整数的阶乘不对?
元知元能1296
1就是时间开玄,0就是空间闭合,1和0就是时空,大道至简,时空是宇宙高等文明编程的秘密武器
深水码头
0个感叹号,咋么可能等于1。真是谬论
Loading.....
这边有0根铅笔,你排列一个给我看看
连杰12
好文分享一下你的
大漠烟直
泰勒幂级数中阶乘一大串[呲牙笑][呲牙笑]大概意思任何函数都可以分解为多项式的和[呲牙笑][呲牙笑][呲牙笑][呲牙笑]
看我IDnmsl
阶乘是啥[得瑟]
语很鱼
有个屁用,否则,证明一下。
字母数字界第二
这个是规定的可去间断点
!!!
0/0=多少?
吾梦以乱红尘
0!的意义是从0个样本中选出0个样本进行算排列。有1种排法。所以0!=1。排列结果就是空集本身。