我们上回列出方程组(4元2次):

需要根据这组方程求出m。
首先,把(2)和(4)中的1/2都划掉(这是把等号两边同乘以2的结果),得到新的(2)和(4):

把(1)改写成

把(2)改写成

对比(5)和(6),你能想起什么?能不能想起平方差公式?

这个恒等式中的3个角色,在(5)和(6)中出现了两个,我们不由不想起它。这就像看到“高”“烈”“兴”,立即想到“兴高采烈”一样。
下一步就好办了。用(6)除以(5),

这个关系多么简单!它是利用了(6)式以后得到的,有了它,我们就不用理会那讨厌的包含二次方的(6)式了!
我们只需要关注(5)和(7):

其中v1是与氢原子核碰撞后未知粒子的速度,我们对它不感兴趣(因为题目没叫我们求它) 所以,我们来把它消掉!(消元法)
做法是,先用别的量,把打算消掉的量(v1)表示出来。我们选(7)式,由它推出

再将(8)式代入(5)式中,

你看,那个我们不感兴趣的v1消失了。
对方程(3)和(4),只需要“如法炮制”。实际上,我们根本不需要把刚才的步骤再重复一遍,而可以根据(9)直接写出结果。
因为,(9)式是对未知粒子与静止氢原子核正碰的分析结果。对未知粒子与氮原子核正碰的情况,只需要把(9)中的氢原子核质量,换成氮原子核质量,把氢原子核被碰撞后的速度,换成氮原子核被碰后的速度,就可以了(轻松愉快):

对比(9)和(10),既然它们左边相等,那么右边也相等:

(注意,这个式子中只有m一个未知量了!它只是一个简单的一元一次方程)
整理得到
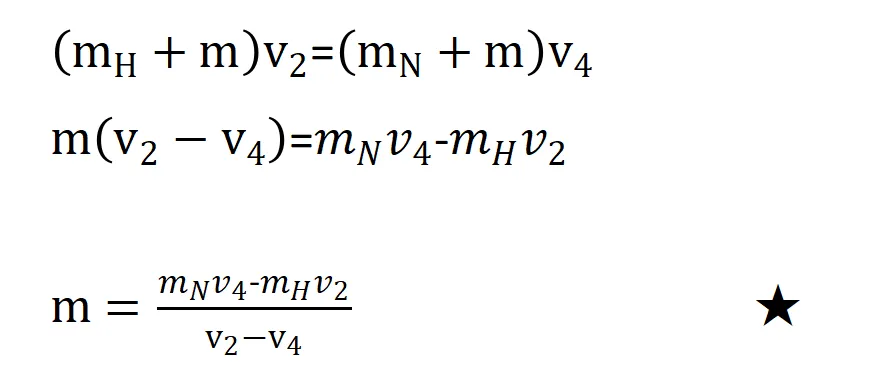

原来,这种未知粒子的质量就等于氢原子核的质量!
虽然题目没叫我们求未知粒子在碰撞前的速度,不过,既然已经求出它的质量,不妨再把它的速度v算出来(假如不是在考试)。
选哪几个方程计算v呢?可以选(5)(7),令(5)中的m等于mH,两边的mH约掉,得到

最后注意:我们一直是用字母进行推理,直到我们用题目中的已知量表示出m时,才把已知数据代进来进行计算。
在此之前,我们脑子里压根不用惦记什么4.4乘以10的多少次方,氮原子核质量是氢原子核质量的14倍之类。——我们进行推理的时候只用字母,清清爽爽。
有些学生在一开始列方程的时候,就把题目中的数值写出来。绝对要避免这种做法。
