熵是热力学中的一个重要的概念，也是一个难以理解的概念。就像我大学物理老师常说的：

这个世界上（可能）只有4、5个人真正懂熵，我不属于他们。

与质量或能量等其他量相比，熵似乎是一个主观量，它是观察者定义的宏观变量。热力学第二定律似乎是驱动宇宙的基本定律。每当我深入思考这些问题时，我就觉得更加困惑。

什么是熵？

熵最初是由克劳修斯在19世纪50年代初提出的，用来描述不可逆过程中的能量损失，它对预测系统的自发演化（如化学反应、相变等）非常有用。那个时候，熵更像是一个抽象的数学产物，没有从物理上解释熵到底是什么。1877年，统计热力学的创始人玻尔兹曼，提出了熵的一种优雅的形式。他将熵S定义为一个系统“可能微观排列的数量”的度量Ω，这些排列符合系统的宏观条件（观察到的宏观状态），例如温度、压力、能量：

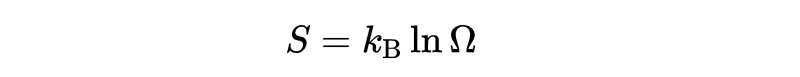
其中kB是玻尔兹曼为匹配克劳修斯熵而引入的常数。

换句话说，玻尔兹曼熵代表了一个系统的隐藏信息，即Ω越高，我们对它的真实微观状态了解得越少。例如，当前宇宙中熵最高的物体之一是黑洞，因为它们的宏观状态仅由它们的质量、电荷和自旋来定义。

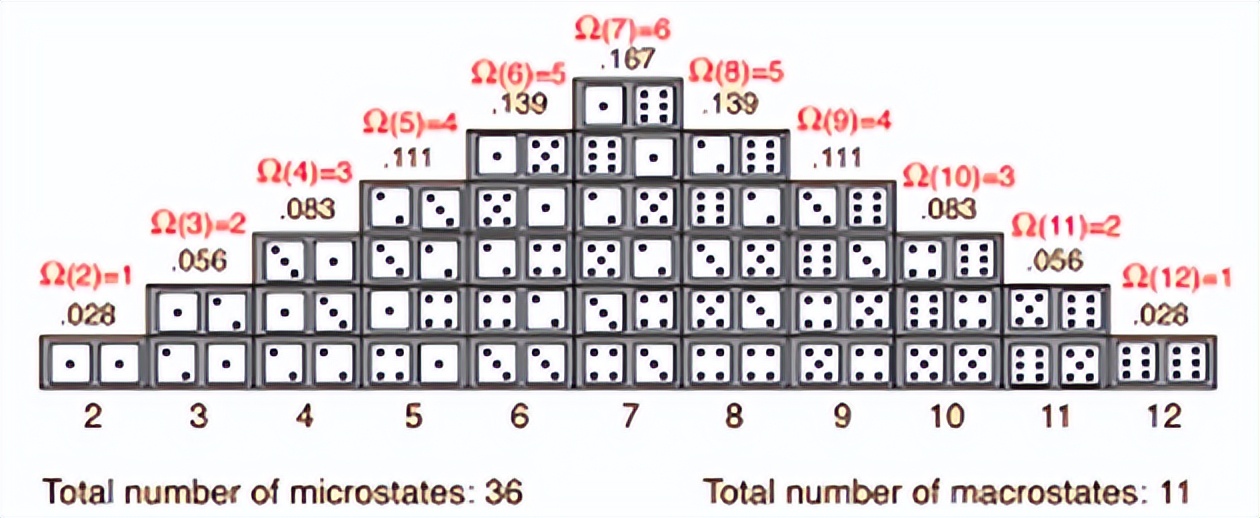
有两个骰子的系统的每个构型的熵，观察到的宏观状态是它们的和。

20世纪中期以来，熵的概念在信息论和量子力学领域也有应用，但不在本文的讨论范围之内。

熵不是无序

关于熵，最大众的解释之一是它代表无序。它来自人的直觉，即我们认为的“混乱”系统通常比有序系统具有更多可能的“排列”，因此熵更低。然而，秩序的概念是主观的，有几个反直觉的例子可以说明为什么将熵描述为无序是不合理的：

我们通常认为一个系统的晶体形态比它的流体形态更有秩序。然而，在相同的热力学条件下，一些系统的晶体形态比其流体状态具有更高的熵。

当相互作用由引力主导时，均匀分布的物质是不稳定的（最不可能的状态），因此具有非常低的熵。具有高熵的最可能的状态是那些物质都聚集在大质量物体中的状态。

热力学第二定律只是一个概率推理

根据主流说法，由热力学第二定律可知“封闭系统的熵只会增加”。然而，这实际上不是第二定律的内容。正确的说法是：

当一个热隔离系统从一个热力学平衡态A过渡到另一个热力学平衡态B时，其热力学熵的增量S大于等于0。

这里的关键是，熵在热力学平衡之外并不是一个正确定义的量，这是一个研究人员仍在讨论的话题。不过，非平衡熵可以在特定的系统中定义，其中我们有一组宏观变量，可以在每个时间点连续监测。然后，熵从与这些宏观变量相匹配的可能微观状态的数量中定义，而第二定律从概率推理中自然出现

系统的大部分时间都处于最可能的状态，与可能的微观状态数量最多的状态相匹配。

例如，对于一个在盒子中扩散的粒子的简单系统，这些宏观变量可以是盒子中每个“网格”中的粒子数量。那么，最可能的构型（状态）是粒子均匀分布的构型，即每个网格中粒子数量相同。为了可视化，我做了一个简单的模拟，100个粒子从一个角落开始，扩散到整个房间。

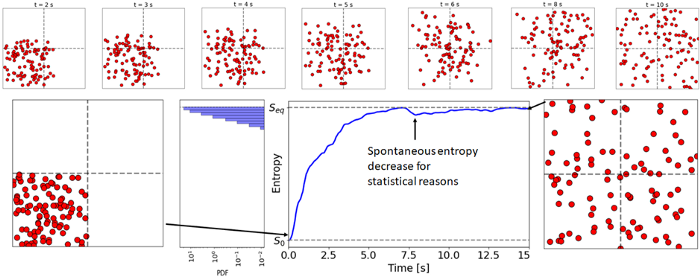
在盒子中扩散的粒子的熵增加（通过伦纳德-琼斯势相互作用）。

通过初始化角落里的粒子，系统从一个非常不可能的低熵状态开始。然后粒子在房间里扩散，熵迅速增加。但有时，更多的粒子会出现在一个角落里（比期望值高），从而暂时降低了熵（涨落定理，这一现象的定量形式）。这就是我之前关于第二定律的观点。

在这里，我定义了一些“网格”来计算熵。实际上有更高的复杂性，例如，如果降低网格分辨率会怎样？这对熵的计算有什么影响？这如何推广到任何物理系统？下一篇文章将讨论这个问题。

时间之箭，从大爆炸到热死

根据热力学第二定律，宇宙的熵一直在增加，并将继续增加，直到达到其最大熵状态的热力学平衡。有趣的是，这种不可逆性在时间的流动中创造了一种不对称（与三维空间相比，每个方向都是对称的）。通过回溯到宇宙的早期，我们可以得出这样的结论：它从一个非常低的熵态开始。那么，我们该如何解释呢？

（部分）答案是宇宙膨胀。在最初的瞬间，宇宙进入了一个指数增长的阶段，由一个高的宇宙常数（比它现在的值高20个数量级）主导。在这一阶段，物质扩散得太快，引力无法发挥重要作用，因此宇宙暴胀期间的最大熵状态是物质的均匀分布。然而，在大约1/10^35秒的膨胀后，宇宙增大了10^26倍，宇宙常数突然衰简到当前值并且扩张停止。

在那之后，引力开始发挥作用，宇宙不再处于热力学平衡状态。物体开始聚集在一起，形成后来的恒星、星系和黑洞，从而极大地增加了宇宙的熵（当引力占主导地位时，均匀分布的物质是不稳定的，因此通常具有较低的熵）。

关于宇宙的未来，所有物质坍缩成黑洞只是时间问题，黑洞会通过霍金辐射蒸发。预计最后的黑洞将在大约10^100年之后消失。在那之后，宇宙将主要由光子和中微子组成，非常接近它的最大熵状态，通常被描述为热死亡。

自发的熵减少

热力学第二定律有一个重要的微妙之处。正如我们前面所讨论的，在大的时间尺度上，熵可能会自发地减少到一个很低的值，仅仅是出于统计上的原因。例如，如果你等了非常、非常、非常长的时间，你房间里的粒子可能会自发地跑到角落里。

这被称为庞加莱始态复现定理，它表明某些动力系统将总是在有限时间后返回到它们的初始（低熵）状态。这并没有违反第二个定律，即“一个系统将在其最可能的状态下度过大部分时间”。换句话说，在很长一段时间内，系统只会在一小部分时间内处于低熵状态。因此，第二定律是关于统计的，而不是关于确定性预测的。然而，由于庞加莱始态复现定理涉及的时间尺度通常比宇宙的年龄大得多，第二定律在实践中变确定，我们恢复了克劳修斯和卡伦引入的经典热力学形式。

有趣的是，遵循同样的思想，任何大小的宏观物体都可以通过量子涨落在真空中自发出现。

一个人的身体可能在大约10^(10^69)年后出现，在我们的可观测宇宙的某个地方。同样的计算也适用于任何人类大小的原子组合。

一个新的早期宇宙可能在大约10^(10^(10^56))年后出现。所谓新宇宙，我指的是大约10^80个原子被包裹在一个非常小的体积中，从而在该区域创造出与我们早期可观测到的宇宙相似的条件。

玻尔兹曼设想，我们的宇宙可能在很久以前就达到了热力学平衡，并达到了最大熵状态，但自发的熵下降到早期宇宙的水平是在极长一段时间之后发生的，这只是出于统计上的原因。然而，这些计算所涉及的时间尺度是如此抽象，人们难免会怀疑这是否有任何意义。

结论

我试图提供一个关于熵和热力学第二定律的直观理解。但实际上，有几个问题没有在本文中得到解决。例如，当我们计算这些粒子在盒子中膨胀的熵时，我们定义了一个2x2的网格来计算熵。然而，如果我们使用其他网格，将得到不同的结果。因此，熵似乎是一个主观量，它取决于观察者选择定义的宏观变量。那么我们如何客观地定义一组宏观变量来计算它呢？深入研究这个问题是相当复杂的，我只是触及了表面。