「Python数据科学」多维数组ndarray对象重塑的常用方法

前面的文章中，我们已经将ndarray的内部机理、0拷贝的视图机制、数组数据的存储顺序等，进行了简单介绍。也通过newaxis的引入，介绍了简单的数组升维的方法。今天来介绍下对多维数组ndarray对象进行更灵活的重塑的常用方法。

本文的主要内容有：

1、reshape()方法

2、resize()方法

3、flatten()方法

4、ravel()方法

为了能够进行多维数组的运算，在很多情况下，都需要对多维数组进行形状的重塑，NumPy提供了多种用于形状重塑的方法：

下面就来对这些方法进行逐一介绍，其中resize()方法被归类到增加或者删除数组元素的主题中，但是，该方法本身也是可以起到修改数组形状的作用，所以，也在这里进行介绍。

在介绍这些方法之前，需要说明的是，NumPy中很多方法是ndarray对象所提供的方法，但是NumPy模块中，有时也会提供同名的函数用于实现相同的功能，在真正使用时，两种方法都是可以的。

首先看下官方文档中关于reshape()方法的说明，为了方便介绍，这里放的是NumPy模块中的reshape()函数，两者功能是相同的。

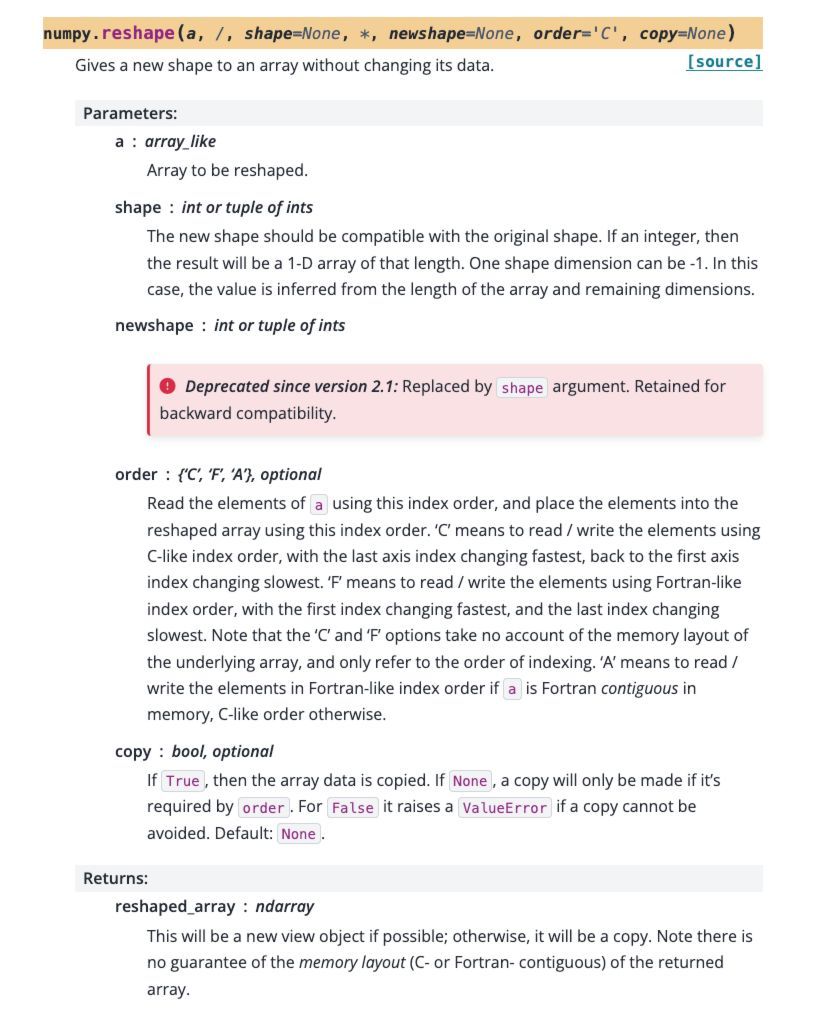
从文档中，可以看到reshape()方法主要有以下参数：

1、shape参数：用于指定重塑后的数组的新形状，可以是整数或者整数元组。需要注意的是，新形状必须与原形状是兼容的，否则会报错。

2、order参数：用于指定数组的读取/写入的顺序，可取的参数值有：

1）'C'：C语言的数据顺序，也就是Row-Major顺序，最后一个轴的数据索引变化最快，第一个轴的数据索引变化最慢。

2）'F'：Fortran语言的数据顺序，也就是Column-Major顺序，第一个轴的数据索引变化最快，最后一个轴的数据索引变化最慢。

3）'A'：保持原始顺序不变。

3、copy参数：bool类型，用于指定数组是否进行复制。

如果形状不兼容的话，则会有如下报错：

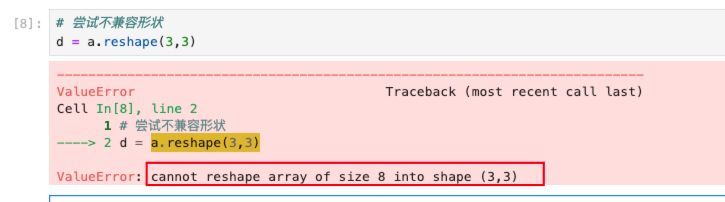
简单总结一下reshape()的使用：

1、通常用于创建一个原始数组的新视图，也就是数据是共用的。

2、新形状必须兼容，否则报错。

3、可以通过copy参数自行选择是创建视图还是拷贝数组。

接下来看下resize()方法：

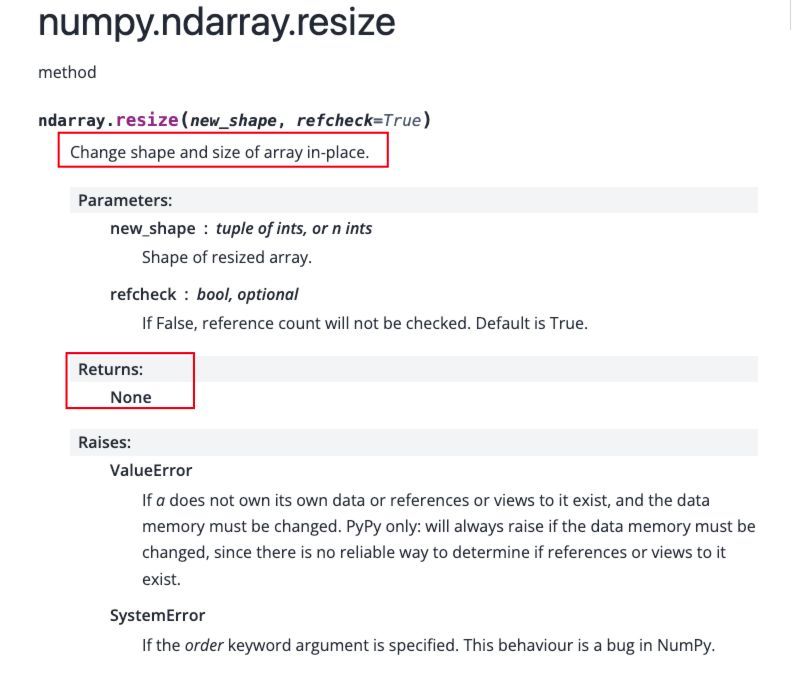
首先需要注意的是ndarray.resize()方法与numpy.resize()函数，这里的行为是有所区别的，我们通过代码来进行演示：

简单比较一下numpy.resize()和ndarray.resize()：

1、ndarray.resize()方法，会直接对原数组进行原地修改，不是创建新视图，所以返回值为None。

2、numpy.resize()函数，会创建原数组的拷贝，而不更改原始数组。

3、ndarray.resize()方法，当形状变大时，会填充0元素。

4、numpy.resize()函数，当形状变大时，会填充原数组的片断，相当于复制填充的做法。

此外，ndarray.resize()方法，由于会对原始数组进行修改，所以需要对原始数组的引用进行检查，多个引用时，可能会报错，所以，如果明确要修改，需要指定参数refcheck=False。

比如：

这个方法比较简单，直接通过代码演示一下：

这里，可以更加清楚看到数组拉平之后的数据顺序。

此外，ndarray还有一个flat属性，属性存储的是在原始数组上的1维迭代器：

同样，通过代码演示一下：

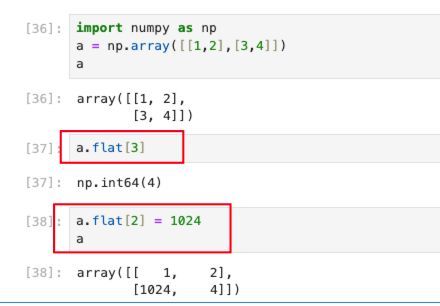
可以通过flat属性，对原始数组进行遍历、索引和修改。

除了ndarray.flatten()方法外，还可以通过numpy.ravel()函数来将数组拉平。

同样，通过代码进行演示：

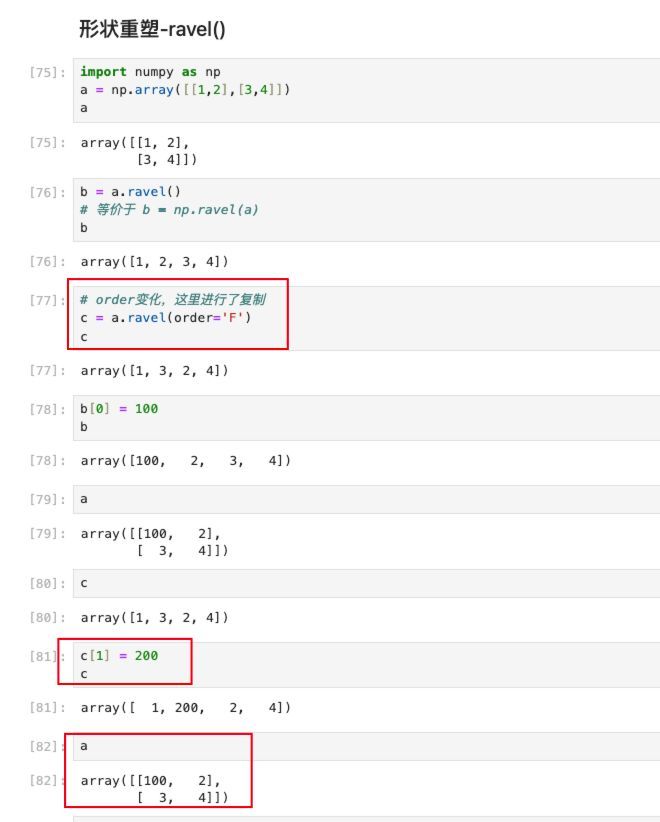
从代码中可以看到：

1、ravel()方法可以实现对原数组新建视图，由于共享原始数据，所以相较于flatten()方法总是复制数据而言，ravel()方法效率更高。

2、ravel()方法在必要的时候，也会创建数据副本，比如数据存储顺序发生改变时。

本文介绍了常见的对多维数组ndarray进行形状重塑的方法，其中：reshape()默认会返回新的视图，原始数据不变，但是需要保证形状兼容；resize()直接修改原始数组的形状，可能会修改原数据；flattern()返回一个新的拉平的数组，不共享原始数据；ravel()则返回扁平化的视图，共享数据。此外，flat属性，是一个对原始数组进行扁平化访问的迭代器，可以对原始数组直接进行遍历、读取、修改等。

以上就是本文的全部内容，感谢您的拨冗阅读！