关于平面内的透视仿射有如下两个定理。
定理一:平面内的透视仿射由一对对应轴与一对对应点完全决定
证明:设已知对应轴g与不在其上的一对对应点A,A',B为平面上任一已知点




上述过程表示,只要知道任何一个点A通过对应轴g仿射后得到的点A',其它点的仿射位置就也可以确定下来。
定理二:给定平面内的两个三角形,至多利用三回透视仿射可使一个三角形变为另一个三角形。

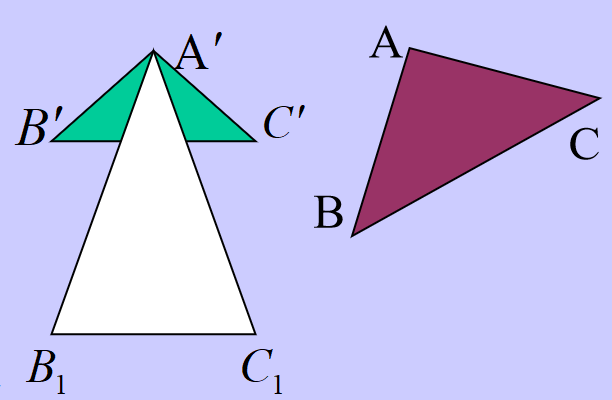



从以上仿射过程看到,要把一个三角形仿射为另一个三角形,相当于可以每次仿射一个顶点,分三次完成。
自然有以下结论:
若两三角形有一对顶点重合,则利用两回透视仿射就够了。
若两三角形有两对顶点重合,则利用一回透视仿射就够了。
透视仿射在平面内的作用主要体现在图像处理和几何变换中。透视仿射变换是将图像从一个平面投影到另一个平面的过程,涉及旋转、平移和缩放等操作。这种变换在图像处理中有着广泛的应用,可以帮助实现图像的缩放、旋转和变形等效果。
