17世纪末,牛顿提出万有引力定律,从此数学开始展现出对于现实世界的强大统治力。日月星辰都变得有迹可循,并成功预言了海王星的存在.到20世纪初,爱因斯坦先是通过狭义相对论解出了时间膨胀与尺缩效应,并揭示了质量和能量本质上其实是等价的。紧接着又通过广义相对论的引力场方程解出了时空弯曲,并预言了星光偏转、引力红移、引力波以及黑洞的存在,每一个伟大物理定律的提出往往都对应着一个数学公式。通过这些公式,我们可以解释一些已知的现象,同时也能预言一些超出你认知的东西。
多年后,人们一验证,发现居然是真的。于是有人就说,数学是物理学家的工具,是描述大自然的语言。但从种种迹象来看,它似乎不只是一个小小的工具,而更像是自然界的一种基本法则。而这种感觉在你理解了量子力学后则会变得愈发强烈。
薛定谔写下薛定谔方程后,马克斯·波恩很快就给出了波恩解释,即波函数绝对值的平方代表了粒子出现在空间某处的概率。
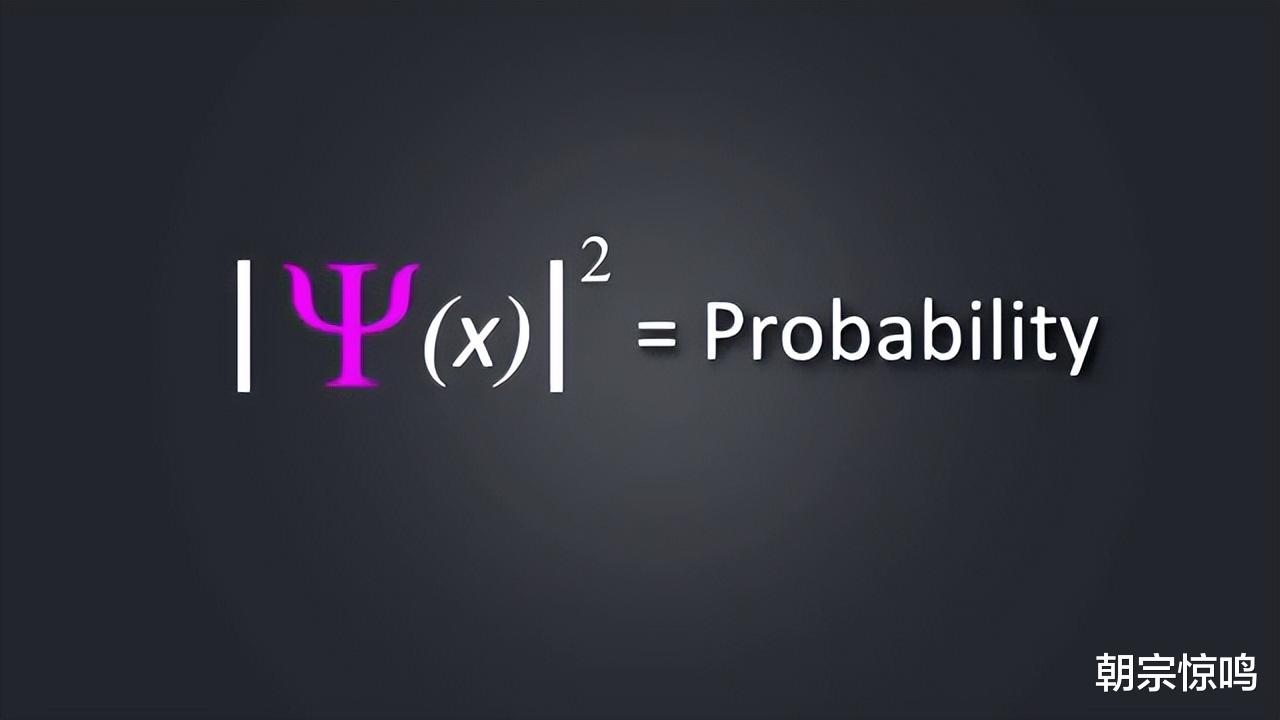
薛定谔方程的整体含义其实就是,动能加势能等于总能量,其中势能包括有电势能、重力势能以及核力势能等等。对于一个不受任何外部作用力的粒子,其势能为零。带入薛定谔方程中解出来的波函数的绝对值的平方是一个常数,也就是说,一个绝对自由的粒子出现在空间中各个地方的概率都一样,他无处不在。

当然,这是理想情况。现实世界总是充满了各种限制。现在我们考虑实际情况,比如一个氢原子的核外电子。对于电子来说,它的势能主要来自于原子核所带来的电势能,越往外,电子的电势能就越大。
原子核外的势能场,就像是一堵厚厚的势能墙,这堵墙内的势能比电子的总能量还要高,我们一般称其为势垒。直觉来看,在不吸收外部光子的情况下,核外电子永远都不可能穿越壁垒逃逸到原子核外。否则,他在逃逸的过程中就会出现动能小于零的情况,这显然不可能。这就好比人造卫星在不主动加速的情况下,永远也不可能克服重力势能逃离地球。

但是永远不要试图以宏观规律来理解微观,一切还得以实际计算结果为准。我们将粒子的势能带入到薛定谔方程求解后,奇迹发生了。为了简化计算,我们直接以一堵墙的形式表示势垒。波函数在遇到势垒时会分化成两个波,一个被墙体反射回去,一个经过墙体衰减后穿墙而过。
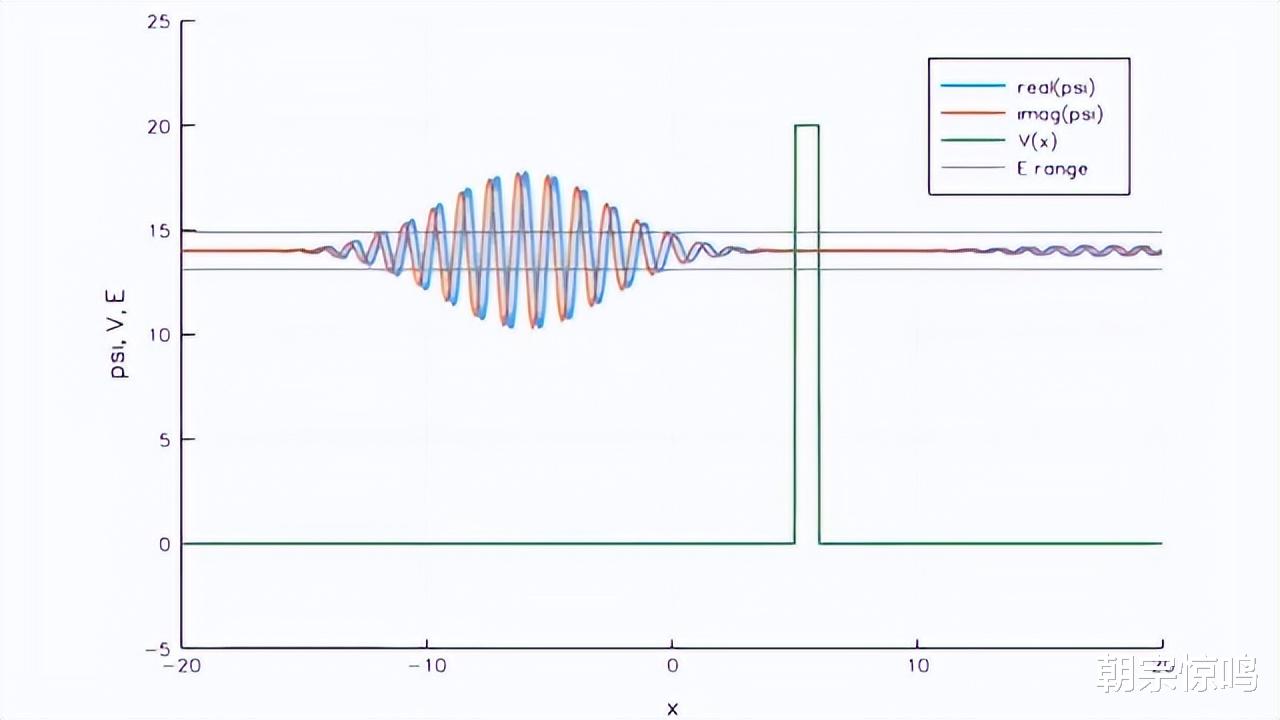
当然,穿墙后波的振幅会比反射回去的波小很多,也就是说,你在右边发现粒子的概率肯定比在左边小,也就是说穿墙的概率并不是很大。但是请注意,这个概率并不为零,量子力学允许一个粒子穿过势能比他自身总能量还要大的墙。
这是什么操作?如果说数学仅仅是物理学家们用的一个工具,那真实世界就没有任何义务必须得遵守这个方程的解。1927年,距离薛定谔方程发表不到一年,就有包括弗里德里希·洪德在内的好几个物理学家都得到了这个穿墙解。
但由于当时人们并不觉得这有什么实际物理意义,从而都选择了忽视。直到1928年,24岁的美籍俄裔物理学家乔治·加莫夫也注意到了这个解。加莫夫是后来宇宙大爆炸理论的提出者之一。

他预言了宇宙微波背景辐射的存在,同时也是科普畅销书《物理世界奇遇记》以及《从一到无穷大》的作者。加莫夫认为这个穿墙解是存在真实物理意义的,因为它可以解释原子核衰变。
我们知道,原子核由质子和中子组成,质子和中子由四大基本相互作用中最强的强相互作用牢牢粘在一起。既然这个力如此之强,那为什么有的原子核有时候还会释放粒子发生衰变呢?
加莫夫通过一系列的计算发现,原子核实际衰变的概率和方程解出来的穿墙概率完美符合,也就是说,微观世界真的能穿墙。人们将这个现象称之为量子隧道效应,也叫量子穿隧。
其他的物理学家在听说了这个量子穿隧后,纷纷开始研究。这一研究可不得了,因为人们发现他简直就是无处不在。比如说核聚变,核聚变其实就是把两个小原子核合并在一起,形成一个大原子核的过程。
这期间会释放出大量能量。太阳之所以能发光发热,不是因为他燃烧得热烈,而是因为它里面时时刻刻都在发生着大量的核聚变反应。但问题来了,我们知道,原子核都带正电,由于同性相斥,两个原子核在逐渐靠近时,所受到的斥力就越大。
只有当他们跨越某个距离临界点时,才会进入强力的统治范围,从而被牢牢的粘在一起。但前提是你得跨得过去才行,这就需要原子核具有非常高的动能。微观粒子的动能表现在宏观,就是温度。太阳核心温度大约在1500万-2500万摄氏度,除去压强等其他因素外,这依然还远远达不到实际氢核聚变所需要的温度。而正是因为量子隧道让太阳内部的核聚变在温度不太高的情况下,实实在在的发生了。换句话说,我们如今能享受太阳的光和热,还多亏了有量子隧穿。
同时,量子隧穿在生物领域也比比皆是。植物能发生光合作用,生物酶能提高生物体内的反应速率,遗传物质能够自我修复等等,都离不开量子隧穿。你可能在中学物理课上还听说过扫描隧道显微镜。据说可以通过它看到原子排列的图像。事实上,它并不是像寻常显微镜那样的光学仪器,它所展现出来的只是原子表面电子发生量子隧穿的概念。具体原理是当探针接近金属表面时,探针和金属表面之间存在一个非常非常小的空隙。
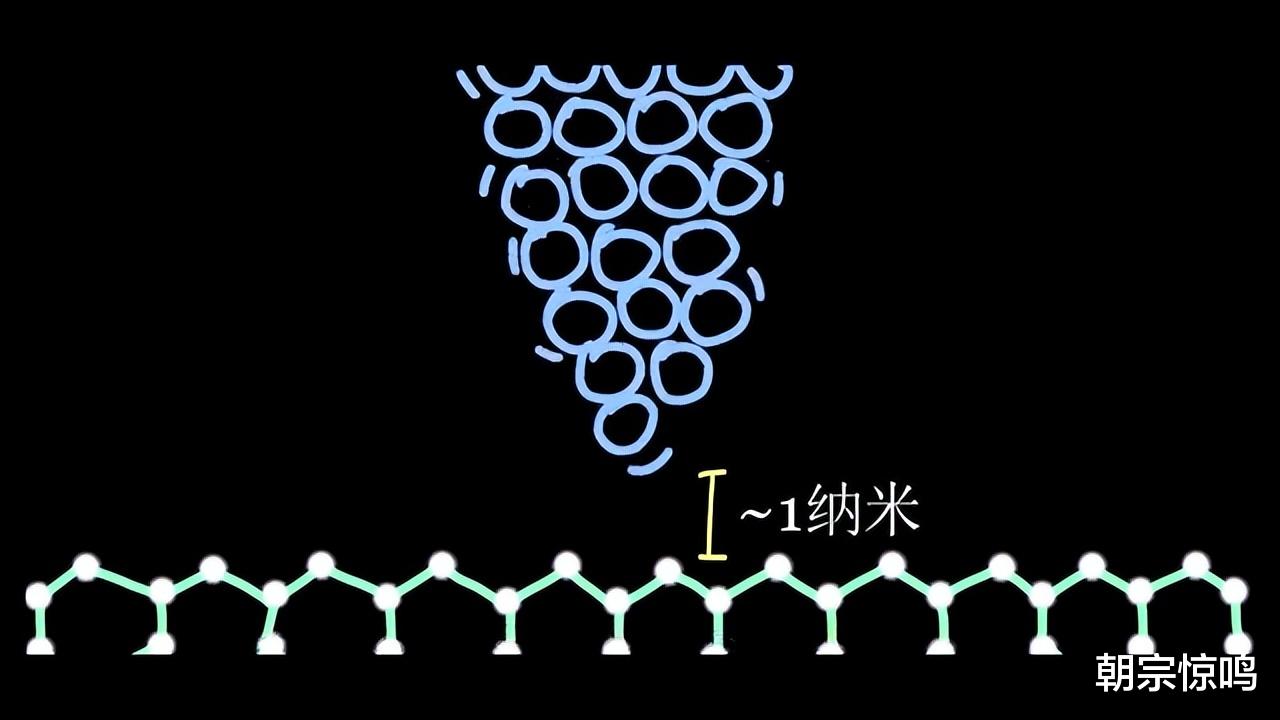
这个空隙就相当于一堵薄薄的壁垒,金属表面的电子原本是无法克服空隙,逃离原子核的。但由于量子隧穿效应,电子现在就有可能会穿越这个缝隙,跑到探针上去。于是探针就探测到了电流。原子不同的高低排列,与探针之间形成不同的距离。不同的距离就好比不同厚度的墙,不同厚度的墙对应着不同的穿墙概率。于是扫描隧道显微镜就能根据这个概率精确还原出金属表面原子排列的图像。

现在量子隧穿虽然是实锤了,但这里面有个疑问。既然E<V粒子为什么还能穿墙呢?难道能量守恒定律在穿墙的那一刻被推翻了吗?其实并没有。首先,粒子在隧穿前和隧穿后的整体能量,包括动能和势能,必须是一样的,否则就无法完成隧穿。这一点并不违反能量守恒。你感到奇怪的点在于,它到底是如何拥有超过墙壁势垒的能量值去穿过它的。这里大概有两种解释。
一种解释是,我们知道,能量和时间之间满足一个不确定性原理。在时间间隔非常小的区域内,量子系统的能量可以有一个小小的波动。只要时间足够长,波动的次数足够多,总会有一次能量正好够用,从而完成穿墙。这就像是从虚空中借来了一部分能量,然后在穿墙后再归还回去。

另外一种解释是,我们之所以觉得它违反了能量守恒,是因为我们在理解量子隧穿时,脑海里仍然会将其类比为容易理解的宏观现象。
比如一个速度较低的小球翻越一个高坡。但实际上,微观世界里的粒子在被观测前并没有一个确定的位置,而是一种概率分布的形式弥漫在整个空间中。这个概率分布由波函数描述。而波是可以穿墙的,就像电梯可以屏蔽电磁波,但实际上并没有完全屏蔽。电磁波波长越长,其穿墙性能就越好。这是波的特性。概率波,作为一种波,也同样如此。所以从波的角度来看,粒子其实并不存在什么跨越高峰,穿越势垒的动作。既然波函数本来就允许它有一定的概率出现在这里,那为什么不可以呢?
看到这里,脑洞大的朋友可能会问,既然量子隧穿来自于薛定谔方程,而薛定谔方程并没有说只适用于微观世界,那作为宏观物体的人是不是也有一定的概率完成穿墙呢?理论上,如果把人的质量带入到薛定谔方程中,求解确实也有一个不为零的概率。但这个概率实在是太小,以至于就算你从宇宙诞生之初就开始每秒钟撞一次墙,到现在也不会有一次成功。但即便如此,量子隧穿仍然给我们带来了一个启示。
一开始,量子隧穿只是薛定谔方程的一个奇怪的解。后来加莫夫找到了这个解对应的实际物理意义。似乎只要是数学允许的事情就皆有可能发生。而这种数学先于实验的现象在后面量子力学的发展中可谓是家常便饭。这让我们不得不认真思考,数学和现实宇宙到底是怎样的一种关系。
