时空图是狭义相对论中时空性质的图示。时空图允许定性地理解相应的现象，如时间膨胀和长度收缩，而不需要数学方程。在时空图中，一个物体在所有时间内的位置的历史轨迹会形成一条线，即该物体的世界线。时空图中的点表示空间和时间中的固定位置，称为事件。

最著名的一类时空图被称为闵可夫斯基图，由赫尔曼·闵可夫斯基在1908年提出。闵可夫斯基图是一种二维的图，它描述了发生在一个由一个空间维度和一个时间维度组成的宇宙中的事件。与常规的距离-时间图不同，距离显示在水平轴上，时间显示在垂直轴上。此外，时间和空间测量单位的选择是这样一种方式，以光速移动的物体被描绘成与图的轴线成45°角。

如何将四维时空形象化？我们不知道，但我们从霍金的话中得到了启发，他说：

想象四维空间是不可能的。我个人觉得把三维空间形象化已经够难了，然而，很容易画出二维空间的图，比如地球表面。

因此，我们经常使用时空图（也被称为闵可夫斯基图），没有x轴和y轴，通常有一个垂直的时间轴和一个水平的空间x轴。

狭义相对论是建立在这样一个假设上的：对于任何惯性观察者来说，光的传播速度都是恒定的。因此，我们需要能够在时空图上，画出光线的路径。这样的一条射线可以从x轴上的任何一点开始，沿着x的递增或递减方向运动（我们可以想象自己站在x轴的某一点上，沿着x轴向我们的右侧或左侧发射一束光）。

在时空图上画出光线路径的困难在于，因为光的传播速度非常非常快，如果我们用国际单位秒和米作为两个轴的话，表示这条路径的线应该尽可能接近水平线。

为了解决这个问题，我们将以秒为单位的时间乘以以米/秒为单位的光速，并使用这个量ct作为垂直时间轴的单位。ct的单位是光速乘以光传播1米所需的时间t，即1。通过使用时间的ct单位，我们将光速c定义为1，现在可以把光线的路径画成斜率为45度的直线，向左或向右，取决于它的运动方向。

记住，ct中的t仍然是指时间单位秒，但是一个单位的ct不是1秒，而是3 × 10^（-8秒），这个数值要小得多。在相对论中，使用米作为时间和距离的单位是一种方便而普遍的做法。闵可夫斯基空间中的单个点被称为一个事件，它有四个组成部分ct，x，y，z，用指数标记法记作：

其中：

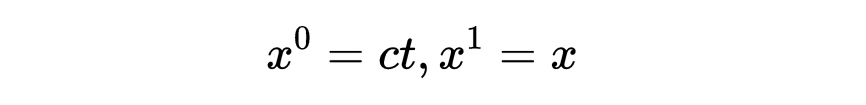
x_μ有也也被称为时空的“四位置”。闵可夫斯基空间中的一条线代表粒子在时空中的运动（有点像蒸汽轨迹显示喷气飞机的路径），被称为粒子的世界线。

时空图的基本概念

坐标系S中观察者的一个简单的时空图

上图表示在惯性参考系S下观察者O的二维时空切片。空间中的单个点是一个事件，它在x的某个值处瞬间发生。例如点(3,2)描述时空中的一个点，它的时间坐标为ct = 3，空间坐标为x = 2。

因为我们使用的是ct时间单位，一条45度的直线表示光线的路径。我们可以画出无数条这样的线，每条线代表从ct = 0时的不同x值开始的光线。以小于c的匀速运动的物体与x轴成大于45度角的直线。

如果一个物体以恒定速度v运动，那么这个速度等于移动的距离除以所花费的时间，得到：

物体将有一条与ct轴夹角θ的直线，其中：

从而：

增加一个观察者

我们如何表示第二个观察者O'所在的惯性系S'呢？首先，为了简化工作，我们假设两个坐标系都是标准构型，并且坐标系S'相对于坐标系S以恒定速度v移动。

我们可以先画出坐标系S'的ct'时间轴。但是我们如何在图中画出这个轴呢?

首先，因为我们使用的是标准构型的坐标系，我们知道坐标系S和S'的原点在坐标系S中的时间ct = 0和坐标系S'中的时间ct' = 0时重合。因此，ct'轴必须通过坐标系S的原点。

其次，考虑当空间坐标x' = 0时，在坐标系S'中可能发生的所有事件。所有这些点连接在一起，就构成了ct'轴。但x' = 0点沿着ct'轴以速度v移动。因此，我们可以画出ct'轴作为移动点x' = 0的世界线。ct'轴与坐标系S的纵ct轴成角度θ：

第二个参考系S'的ct'时间轴

我们现在需要画出坐标系S'的x'轴。这个轴可以将所有的事件连接起来，时间坐标为ct' = 0。但是该怎么做呢？对于ct'轴，我们知道x'轴必须通过坐标系S的原点，因为处于标准构型。

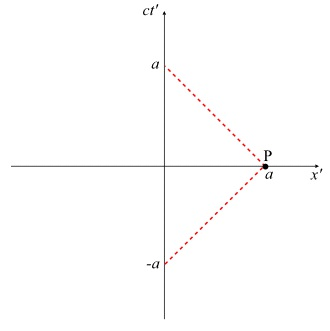
反射光线的路径

回想一下，狭义相对论的一个假设是光速c对所有惯性观察者来说都是一样的。这意味着，对于任何惯性坐标系，任何光线的斜率都是45°。上图显示了观察者O'的时空图（轴ct'和x'）。折线表示x' = 0, ct' = -a处发射的一束光线，照射在x' = a, ct' = 0处的一面镜子上，反射回x' = 0，ct' = a。我们称x' = a, ct' = 0处的点（或事件）为P。随着a的变化，P点的位置也会变化。事实上，由于光速的恒定，对于a的不同值，P点（ct'总是等于0）沿着x'轴移动。

第二坐标系S的x'轴

我们使用点P的这个属性来定义x'轴的位置。这次我们回到了观察者O的参考系S，它显示了在点Q (x' = 0，ct' = -a)发出的一条光线(折线)击中了点P (x' = a，ct' = 0)的镜子，然后反射回点R (x' = 0，ct' = a)。

三角形ORP是一个等腰三角形，被一条与x轴成45°的线平分并穿过O。因此，x'轴与x轴的夹角必须与ct'轴与ct轴的夹角相同，也就是θ=α。

因此我们可以说x'轴的方程是：

而ct'轴的方程为：

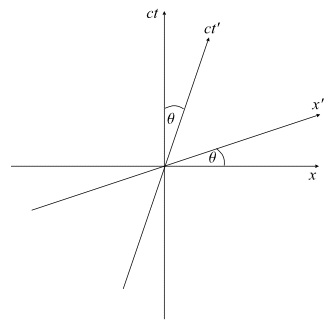
观察者O的时空图

上图显示了从O（从S参考系）的角度来看的参考系S和S'， O'所在的参考系S'向右移动。

同样的物理情况如下图所示，但这一次从O'的角度来看，他看到O向左移动。

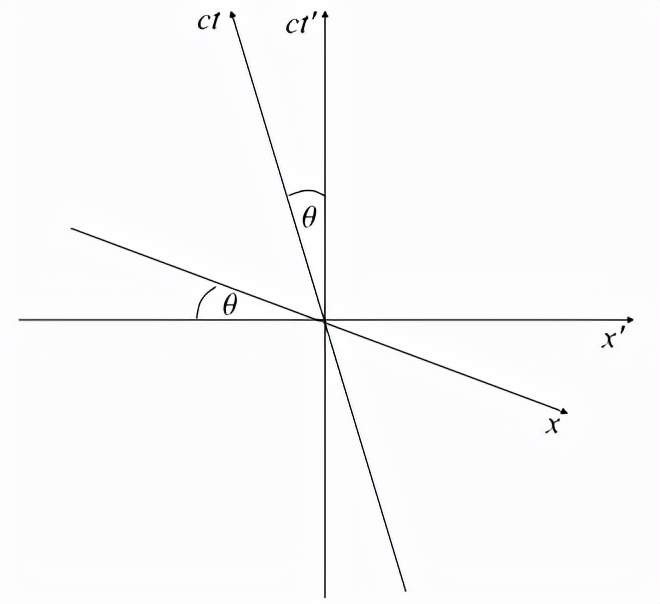
观察者O'的时空图

这可能有点让人困惑。我们有一个惯性系S，它的坐标轴是x和ct，还有另一个惯性系S’（相对于S以匀速v运动）它有自己的坐标轴x’和ct’，都画在同一个图上。我们现在如何描述一个特定事件的坐标？

这是简单的。我们需要做的就是构造平行于坐标轴的坐标线。以下图所示的事件A为例：

我们通常读取A关于x和ct轴的坐标（就像我们在任何笛卡尔坐标上做的那样），它们是x_1和ct_1。然后我们画一条穿过A平行于x'轴的直线。这条线与ct'轴的交点就是ct'坐标，即：

类似地，我们接着构造一条穿过A并平行于ct'轴的直线。这条线与x'轴的交点就是x'坐标：

这里值得注意的是，x'和x轴并不重合。如果我们使用伽利略变换，它们就会重合，当然，伽利略变换是基于伽利略/牛顿对绝对时间和空间的假设。在这种情况下，我们仍然会画一个倾斜的t'轴（其中t' = t），但x'和x轴将在同一条线上（其中x' = x - vt）。

第二个假设（光速的恒定）要求有一个倾斜的x轴，并破坏了所有关于绝对时间和空间的假设。根据绘图的准确性，并假设我们知道如何校准ct'和x'轴，我们可以估算出观察者在S和S'参考系上测量到的事件A的坐标。从图表中测量当然不是很准确。后面，我们讨论洛伦兹变换，它允许我们用代数方法计算在不同惯性系中的观察者的测量值，包括校准ct'和x'轴。

同时性与因果关系

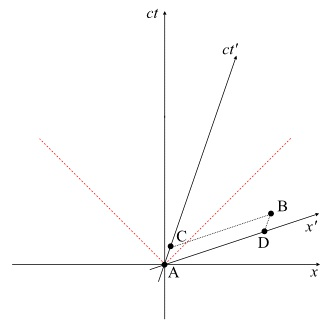
同时性的相对性

我们现在可以证明一个令人惊讶的结果，即事件的同时性可以依赖于观察者的参照系。上图显示了四个事件A，B，C，D。它们发生的顺序是什么？

惯性系S中的观测者O将按照A、C、D、B的顺序（随着时间ct的增加）分别看到事件的发生。然而，惯性系S'中的观测者O'将使用ct'轴来记录他的时间，首先会看到A和D同时发生，然后看到C和B同时发生。由于两个观察者不共享一个共同的时间轴，一个观察者同时发生的两个事件对另一个观察者来说也不可能同时发生。这种现象被称为同时性的相对性。

如果两个事件同时发生在空间的同一点上，所有的观察者都认为它们是同时发生的。如果事件在空间中是分离的，那么它们是否同时发生取决于观察者的参照系。

我们还可以从上图中看到，两个观察者不仅会在哪些事件是同时发生的问题上产生分歧，而且在C和D的情况下，他们甚至不会看到事件以相同的顺序发生。这个结果比同时性的相对性更奇怪，因为它似乎推翻了因果关系的基本概念。事件X只能导致事件Y，如果X发生在Y之前。假设X是我掉书的事件，Y是书掉到地板上的事件。如果一个观察者不能同意我的观点，我们可能会以一种奇怪的情况结束，他们先看到书掉到了地上，然后看到我掉了一本书。

幸运的是，狭义相对论的结果之一是，在观察者的惯性系中，没有任何信息信号或物质物体的传播速度能超过光速。这意味着，尽管观察者可能对两个事件的顺序有不同意见，但他们不会对两个由光信号联系起来的事件的顺序有不同意见。

在观察者的惯性系中”的条件是至关重要的。在不断膨胀的宇宙中，正如我们在宇宙学中所看到的，星系可以以大于光速的速度远离我们。然而，这种运动并不在任何观察者的惯性系中，因为它是空间本身在膨胀。

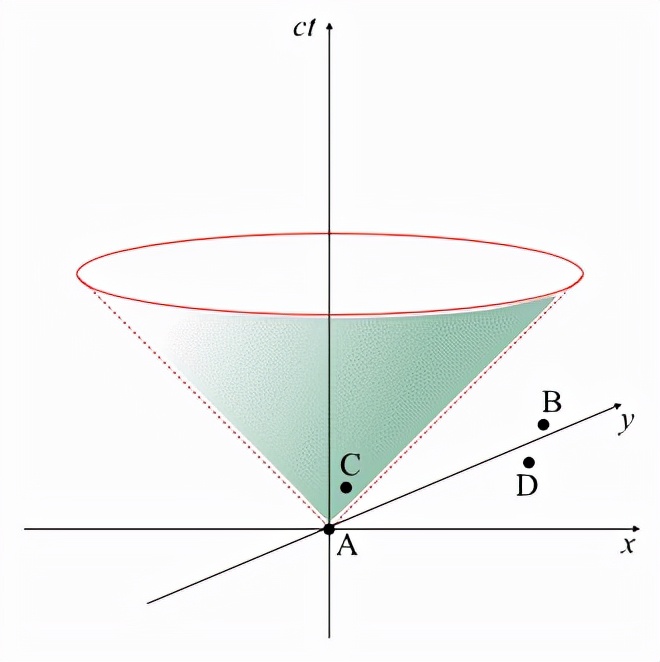
光锥

光锥是由通过A的光线（两个虚线）绕ct轴旋转而形成的（y轴表示光锥占据了两个空间维度:x和y）。假设这四个事件仍然位于x轴的正上方，我们现在看到，在B、C和D之外，唯一可以通过不超过光速的信号与A联系在一起的事件是C。这是因为只有C在光锥的“内部”。换句话说，因为没有信号能比光传播得更快，所以A唯一可能引起的事件就是C。事件，比如A和C，位于彼此的光锥内，被称为因果关系。如果两个事件在一个惯性系中有因果关系那么它们在所有惯性系中也有因果关系。

如果任何事件，如B，在A的光锥内，可以通过A（一个事件在原点）和B画一个ct'轴。这意味着有一个惯性系，A和B在不同的时间出现在相同的地方。

相反，只有比光速快的信号（与x轴成45°的直线）才能将A和B, A和D, C和D联系起来。所以这些事件没有因果关系。由于C和D之间没有可能的因果关系，因此，在任何参考系下，我的书都不会在掉到地上之前就掉到地上。

如果任何事件，如C，是在A的光锥外，则有可能通过A（在原点的事件）和C画一个x'轴。这意味着在某个惯性坐标系中，A和C同时发生但在不同的地方。

光锥（上图）在相对论中是一个非常有用的概念，它在三维空间中显示了那些事件的位置，这些事件可能与现在发生在原点的事件有因果关系。光锥的侧面是由穿过原点的光线形成的。原点下方的锥体表示过去可能导致原点事件的事件。原点上方的锥体包含可能由原点事件引起的事件。一个通过原点和x、y轴的平面代表现在。

间隔不变性

观察者O和O'将使用不同的坐标值描述上面提到的四个事件A、B、C、D的位置。但是，他们会同意两个事件之间的时空分离，其中间隔∆s^2为：

这个定理被称为间隔的不变性，我们将在后续的文章中用洛伦兹变换来证明它。我们说间隔是不变的，因为任意两个不同的惯性观测者计算∆s^2，将得到相同的答案。

时空间隔∆s^2的值可能是正的、负的或零的，最好把它看作一个单独的符号，而不是某物的平方。在原点处的事件A与时空中其他事件的三种关联方式是：

类时间间隔，其中∆s^2＞0，描述了A光锥内的事件。这些事件与A是有因果关系的，会有一些惯性系，A和C在同一地点，但在不同的时间发生。

类空间间隔，其中∆s^2＜0，描述了A光锥外的事件。这些事件与A没有因果关系，会有一些惯性系A和C同时发生但在不同的地方。

类光间隔，其中∆s^2=0，描述了A光锥上的事件。这些事件与A有因果关系，但它们只能通过一个光信号与A联系起来。

间隔不变性是狭义相对论中最重要的定理。

不变的双曲线

现在我们已经知道，时空间隔对于任何惯性观测者都是不变的，我们可以看到如何在时空图上校准坐标系S'的x'和ct'轴。考虑以下方程：

这两条曲线都定义为观察者O的时空图上的双曲线（奇异双曲线）。如下图所示：

上图显示了坐标系S'相对于坐标系S作匀速相对运动。我们试图校准坐标系S'的ct'和x'轴。考虑穿过事件A和B的不变双曲线：

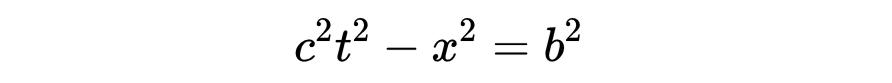
事件A在ct轴上，因此x = 0。如果我们让事件A发生在ct = 1，那么b^2, A到原点的类时分离，也必须等于1。因为双曲线将所有具有相同时空间隔的事件连接起来，所以ct'轴上的事件B （x' = 0）也必须在ct' = 1时出现。

类似地，穿过事件C和D的不变双曲线：

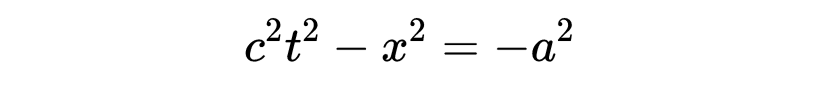
将事件以-a2相同的类空分离连接起来。如果我们让C在x = 1处出现，那么ct = 0，（-a）^2一定等于-1。事件D，在同一个不变双曲线上，也必须出现在x' = 1处（其中ct' = 0）。

注意到D看起来比C离原点更远，尽管它们有相同的时空间隔。类似地，B和A与原点的时空分离是一样的，尽管B看起来更远。这些困惑源于这样一个事实：我们试图在一个平坦的欧几里德曲面上表示非欧几里德时空。我们说的非欧几里得是什么意思？意思是任意两点之间的距离不是由欧几里德线元ds^2 = dt^2 + dx^2表示的，而是由非欧几里德线元ds^2 = dt^2 - dx^2表示的。负号决定了一切。我们可以用不变双曲线来说明间隔不变性的两个重要物理含义：时间膨胀和长度收缩。

时间膨胀

上图显示了在ct = 1处穿过ct轴的不变双曲线，ct'轴在ct' = 1处。通过事件A和C的水平虚线是观察者O的同时线，这意味着该线上的所有事件都具有相同的时间值ct = 1。通过B和D的倾斜虚线（实际上与双曲线B相切）是一条观测者O'的同时线，这意味着这条线上的所有事件都具有相同的时间值ct' = 1。这两位观察者测量到的是什么？

观察者O'测量ct'轴上ct' < 1时发生的事件C。然而，观察者O在其ct轴上测量ct = 1时发生的相同事件。从O的角度来看，S'参考系中属于O'的时钟运行缓慢。黑色箭头TD是O观察到的时间膨胀。

观察者O测量ct轴ct < 1时发生的事件D。然而，观察者O'在ct'轴上测量ct = 1时发生的相同事件。从O’的角度来看，S参考系中属于O的时钟运行缓慢。黑色箭头TD'是O'观测到的时间膨胀。

令人瞩目的结果是，两个观测者都测量到对方的时钟运行得很慢！这种效应被称为时间膨胀。

长度收缩

上图显示了x = 1处经过x轴和x'轴x' = 1处的不变双曲线。垂直的虚线穿过事件B和C，对于观察者O来说x = 1是一个常量。通过A和D的斜线虚线（实际上与D点的双曲线相切）平行于ct'轴，因此对于观察者O'来说x' = 1是一个常量。这两位观察者测量到的是什么？

观测者O'在x'轴上测量x' = 1时的距离OD。点A对于O'也有相同的x' = 1，因为它在直线AD上。然而，观察者O在其x轴上测量的距离与OA < 1相同。从O的角度来看，OD = 1的距离缩小为OD < 1。黑色箭头LC是O所观察到的长度收缩。

观测者O在其x轴上以x = 1测量距离OC。点B的x = 1与点O相同因为它在直线BC上。然而，观察者O'在其x'轴上测量的距离与OB < 1相同。从O’的角度看，OC = 1的距离缩小为OC < 1。黑色箭头LC'是O'观察到的长度收缩。

两个观察者都测量运动物体在运动方向上的收缩，这种现象被称为长度收缩或洛伦兹收缩。

我们必须认识到，时间膨胀和长度收缩都是真实的、可观察到的效应，而不是由错误的时钟、不可靠的尺子或光从一个移动的事件传播到一个观察者所花费的时间造成的光学错觉。一名宇航员乘坐火箭以接近光速飞过地球时，会看到这颗行星沿着她飞行的方向被挤压。

看到被压扁的地球意味着你正在以接近光速的速度移动

当然，我们在日常生活中不会注意到这些现象，因为我们的相对速度并不接近光速。