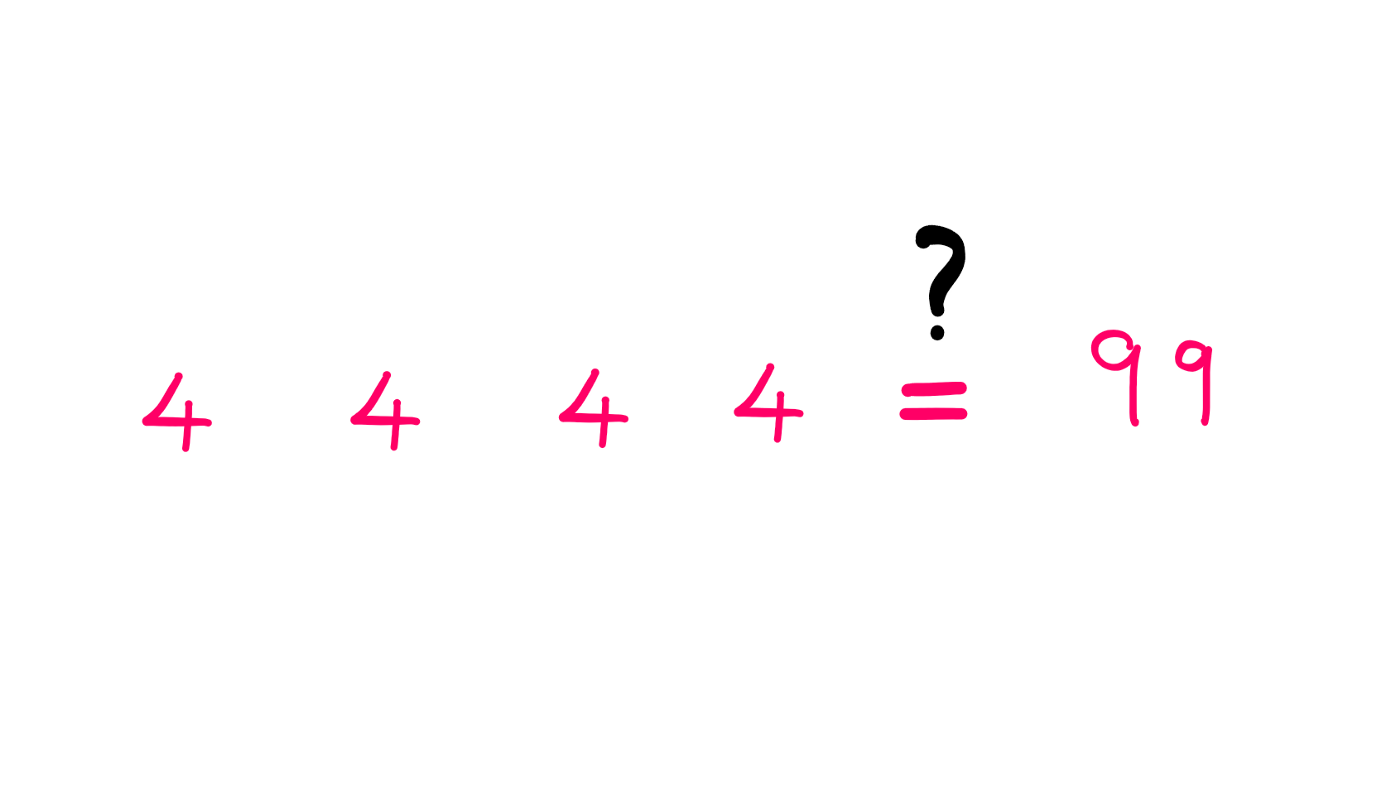
我们将要面临的是“4个4的数学难题”。它的规则非常简单：一行有4个4，用数学运算把这4个4联系起来得到任何可能的非负整数？
从0到9的前10个整数开始。我们先考虑基本运算：加法(+)、减法(-)、乘法(×)和除法(/)。接下来，我将表示更大的整数，但需要更高级的运算符。最后，我将展示如何得到一个可表示任何正整数的通解。
表示前10个整数
前10个整数相对简单。我已经算出了第一个整数0。在此基础上，你可以自己计算出其余的整数（1-9）。记住，对于这些整数，四个基本的数学运算符和括号就足够了。
此外，请注意，这个难题的解决方法并不是唯一的。你的解和我的解不一定相同；有许多方法可以得到相同的结果。
剧透警告：我将直接揭示1-10其余整数的表示方法。
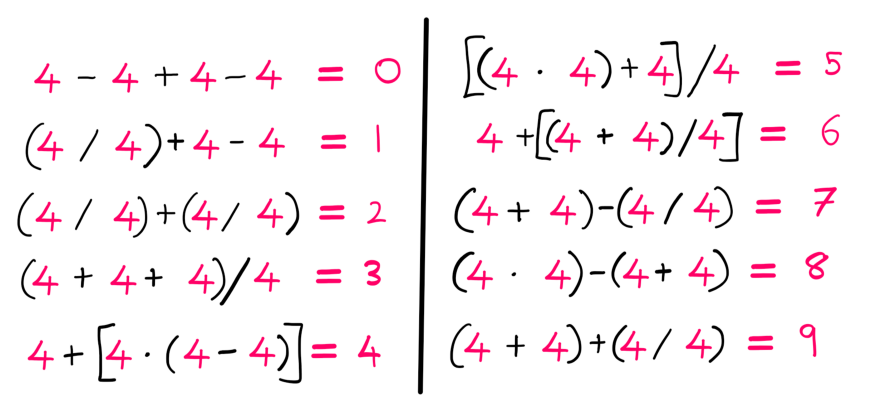
表示更大的整数
一旦我们将范围扩展到10以上，四个基本运算符和括号就不够了。下面是最常用的运算符列（除基本运算符外）。
阶乘：！
百分比：%
根号
小数点
幂
举个例子，考虑封面图提出的问题。
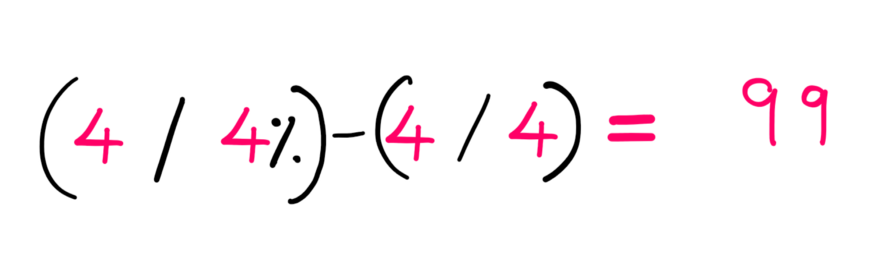
除此之外，一些数学家使用各种各样的其他数学运算符来完成这项工作。但为什么不找一个更一般的解呢？
通解
“4 个 4难题”比较古老（可以追溯到19世纪晚期）。早在20世纪初，著名的物理学家保罗·狄拉克就对这个难题感兴趣，并找到了所有正整数的通解。狄拉克只用对数和根号就解决了这个难题。
为了理解他的天才构思，我们首先需要了解两个基本知识。
第一个仅仅是理解以4为底的对数的运算。数学中，一般不使用以4为底的对数，但对于这个难题，它是有必要的：
第二个是理解以1 / 2为底的对数：
最后，将1/2表示为√4/4（也就是2/4）。现在，我们可以理解狄拉克的通解了，它是这样表示的：
如你所见，这个表达式中有4个4，括号内根号的个数决定了n的值。为了得到任意整数，我们只需要相应地在括号内放置任意多个根号。
garfield
狄拉克是证明了波动力学和矩阵力学在数学上等价的伟大人物
用户11xxx75 回复 03-22 20:59
我怎么记得是薛定谔呢？
丁洋 回复 用户11xxx75 03-22 23:47
薛定谔就是楼主说的波动力学，矩阵力学是海森堡，狄拉克证明了这两个表达式是等价的
风车
第七个对吗？
用户15xxx51 回复 03-22 22:27
什么数?
夜雪花飞
天才！
丁洋
高中数学就能看懂，只是想不到这样做，太他妈天才了！
用户10xxx99
干得漂亮！
叮当不是猫
这么说任何数都可以啊
佑熙驸马 回复 03-25 14:27
前面加个负号会不？
别问 回复 03-23 08:19
任何正数
灰衣
厉害
用户11xxx05
用了对数，根号这些东西，不要说整数了，任何实数都可表示。没意义。
飞龙 回复 04-07 10:52
pi可以用连分式表示
小明 回复 飞龙 04-07 22:38
你是想说连分数吧。
Autumn
收藏了
用户13xxx51
狄拉克伟大的科学家
solutionfail
根号里的2是略写并不是没有……
LOSS
百分比%是运算符号？开玩笑吧！
用户15xxx51 回复 03-22 22:28
是可以这样算的
滿天星 回复 05-02 01:18
％的确可以视作一种运算符号
Said
所以，最后4个4成了根号的配角，对数只是个平台，根号才是主角
楼主的朋友
是谁给的勇气我点进来还看完了？
紫血
这个通解的意思是4的多少次方等于4的n次方，有点脑筋急转弯的意思了
爱我中华
牛逼，这一招学到了
道友请留步
天才
赌棍 低退
总感觉是在侮辱智商
用户15xxx97 回复 05-25 02:05
你有狄拉克的智商混成这样 你爸不抽死你
游戏 回复 04-10 11:59
感觉你好牛逼哦[笑着哭]
流逝的年华
等于5那个为什么要双括？
走遍运河 回复 06-26 21:30
4乘以4的积与4的和等于20，再除以4，等于5
北方神的荣耀
大部分类似问题就知道欺负根号2的2不用写[笑着哭]或者lg10=ln可以凭空变出一个10
星辰幻影1003
[点赞][点赞][点赞]
用户93xxx27
只能说是规矩我定，天下我有
语很鱼
有理数有没有可能是是无理数重叠的结果？？？
滿天星 回复 05-02 01:20
可以去了解一些级数的相关知识，里面就会介绍有理数和无理数的关系，我们常见的无理数e它就是无数个有理数叠加出来的
MMMM我爱你
佩服天才[点赞][点赞]
^二(･ω･)牛^
难道不是任意整数？我直接在任意正数前加一个负号就搞定了！
热心网友
这可以说是是穷举法吗
霸气男爵
还是知识，理解，每一个方式的，知道彼此，所作所为的方式答案
纯钧
根号本身带个2吧
Aurora 回复 04-21 23:41
不要太较真，％的本质还是÷100呢
JYYX
晕，挡住答案，1-10我都花了5-7分钟才做出来，智力真是退化了。
用户10xxx16
为何不对1与3执行法则得任意整数？
深山老林
真他娘的天才[点赞][点赞][点赞]
张小峰
泰勒分解才是真正的神
yxff214
牛逼plus
用户13xxx42
代数，用一个或一组数或符号，代替另一个或另一组数或符号，对1=1进行各种变换推导的科学。
用户16xxx55
5也可以，6也可以。这有何用？
秒天秒地秒空气
这思维逆天了
霸气男爵
怎么去的，怎么来，怎么来就怎么去，怎么得，，
花藏娇
没鸟用
用户35xxx66
10个1也可以，感觉没啥意义
滿天星
当然无理数也可以叠加出有理数
crientuap
ln
7788
那些什么百分号，不是还有100吗？这也算4个4?
用户15xxx51
[点赞][点赞][点赞][点赞][点赞][点赞][点赞]
无限之眼1296
看到数学解算我就莫名兴奋，这就是数学的神之魅力
一棹烟波
以我的数学头脑也就剩下每个月算算花呗账单对不对了[得瑟][得瑟][得瑟][得瑟][得瑟][得瑟][得瑟]
用户13xxx28
根号就是根号2，用了数字2
shhejwj
根号就是根号2
zzxly2
四是四 十是十[呲牙笑]
黄鹏智
这个通解有点赖皮，