如果一个人想理解一个数学结构，例如群或者流形，他要做的第一件事就是找到足够多的例子，有时候例子是很容易找的。然而，时常是这些例子必须要满足的条件相当严格，这时，可能得到的例子会形成一个无限长的清单，使得各个具体例子都包括在这个清单里面。例如，可以证明域F上的任意的n维向量空间都同构于F^n，这意味着只要有一个正整数n就足以完全决定这个向量空间。这时，例子的清单就是

这时，就说得到了相关的数学结构的一个分类。

分类是非常有用的，因为如果能对一个数学结构进行分类，就有了一个新方法来证明关于这个结构的结果，而不必从这个结构所必须满足的公理来导出它们，而只需要检验这个结果是否对于这个清单里的每一个例子都成立，如果是，我们就深信已经一般性地证明了这个结果。这样做并不总是比更加抽象的公理方法更容易，但是有时候确实要容易一些。有一些结果就是用分类来证明的，并且至今还不知道怎样用别的方法证明。更一般地说，对于一个数学结构，知道的例子越多，就越容易思考这个结构 。如果已经知道了一个结构所有的例子，则对于某些目的，就已经完全懂得了这个结构。

有两种典型情况导致有趣的分类定理，这两种情况的界限有时不甚清晰，但是区别仍然足够明显，而值得去加以区别。

作为第一种情况的例子，考虑一种称为正多胞体（polytope）的数学对象。多边形、多面体，以及它们的高维推广都是多胞体。正多边形就是那些所有边长度都相等且所有顶角也都相等的多边形；正多面体就是那些各个面都是全等的正多边形而在每个顶点上又都有相同个数的棱在那里相交的多面体。更一般地说，一个高维多胞体为正，就是说它有尽可能多的对称性，虽然精确的定义还有点难。

在三维情况下，有一个正多面体的新定义，它等价于上面所给的定义，而且比较容易推广∶我们说一个旗（fag）就是一个三元组（v，e，f），其中 v 是多面体的一个顶点，e 是通过这个 v 的棱，而 f 是一个以 e 为边的面。说一个多面体是正多面体，就是说对于任意两个旗（v，e，f）和（v’，e’，f’）都有多面体的一个对称，变v为v’，变e为e’，变f为f’。

很容易看到正多边形是2维的，对每一个正整数k>2，都可以找到一个正k 边形。在3维情况，正多面体就是著名的柏拉图多面体，它们是正四面体、立方体（即正六面体）、正八面体、正十二面体和正二十面体。证明只有这五种正多面体也不算太难，因为在每一个顶点处至少有3个面相遇，而以此顶点为顶的角之和必然小于360°。这些限制表明，过一个顶点的面可以有3个、4个或5个正三角形，或者3个正方形，或者3个正五边形。它们就依次分别给出正四面体、正八面体、正二十面体、立方体和正十二面体。

现在我们想在更高维的空间里找到正多边形和正多面体的类比。刚才定义的正多边形和正多面体中，只有一部分这样的类比很清楚。先看正三角形和正四面体。在R^n中取n＋1个点，使其中任意两点的距离均为1，它们就构成一个正单形（regular simplex）的顶点，这个正单形就是2维的正三角形与3维的正四面体的推广。再看R^n中适合条件

它自然是立方体在高维情况下的类比。最后看R^n中适合条件

就是正八面体在R^n中的类比，因为3维的正八面体

总之，由正四面体、正六面体和正八面体都可以给出可称为正多胞体的一个无穷序列。

除此而外，正十二面体和正二十面体会不会各自也导出多胞体的无穷序列，并可以把它们称为正多胞体这一点并不显而易见，而结果是它们不会。事实上，除了在4维情况下还可以再找到三个例子以外，再也没有其他可以称为正多胞体的例子了。而这三个无穷序列，再加上这三个例子就构成了正多胞体的完全的清单，这三个例子很值得注意，其中一个具有120个“3维面”，各是一个正十二面体，它有一个“对偶”，以600个正四面体为其3维“面”。第三个例子则可用坐标来介绍∶

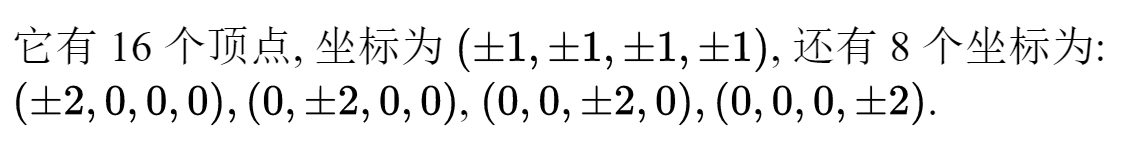
以上就是所有的正多胞体，这一个类比上面简述的3维情况下的结果要难证明得多。这个完全的清单是由施勒夫利在19世纪中叶得出的；考克斯特在1969年证明了，再没有其他例外了。

所以，在3维和更高维情况下，正多胞体分成三个序列（就是n维的正四面体序列、正六面体序列、正八面体序列），再加上五个“例外的”例子，即3维的正十二面体和正二十面体，还有刚才描述的三个4维多胞体的例子。在许多分类定理中，这个情况是一个典型。这些例外的例子时常称为“散在”的例子，时常有非常高的对称性——使我们几乎不敢期望这样高的对称性居然是可能的，如果可能也只是偶然会有的好运气。在不同的分类定理的结果中的这些序列和散在的例子时常互有紧密的联系，这是那些看起来毫无关系的领域互相有深刻的联系的一个信号。

有时，我们并不打算把所有的某一类数学结构加以分类，而是从中识别出某些“基本的”结构，使得其他的结构全可以由它们简单地构造出来。素数的集合就是一个好的类比∶所有的整数都可以由它们以积的方式构造出来。又如，所有的有限群都是一些称为“单群”的基本的群的“乘积”。有限单群的分类是20世纪数学最著名的定理之一。

在数学中有许多这样的情况，两个对象严格地说是不相同的，但是我们对它们的差异并不关心。在这样的情况下，我们认为这两个对象"本质上相同"或"等价"。 这种等价是用等价关系来形式地表示的。

例如，如果两个图形中，有一个图形可以连续地变为另一个，拓扑学家就认为这两个图形本质上是一样的。一个球面在这个意义下与一个立方体（表面）是一样的；我们也能看到，轮胎表面，即环面，和一个茶杯的表面本质上是一样的。直观地说，非常明显，球面和环面本质上是不一样的，但是这一点证明起来就难多了。

为什么不等价比等价要难证明呢？答案在于，要证明两个对象等价，只要找到一个变换就可以证明等价性，而要证明两个对象不等价，就要考虑一切可能的变换。例如，要证明球面和环面不一样，我们怎么能够排除会有一个极为复杂的无法看见的连续变换，可以把一个球面变成一个环面呢？

下面是证明的要点。球面和环面都是紧的可定向曲面的例子，这句话粗略的意思就是，它们都是2维的图形，占据空间的一个有限的部分，而且没有边缘。给定了这样一个曲面，就可以找到一个由三角形拼接起来而且拓扑上与这个曲面相同的等价的曲面。欧拉有一个著名的定理，指出∶

令P为一个拓扑上与球面相同的多面体，并设它有V个顶点、E条棱（边）以及F个面，则V-E＋F=2。

例如，设P为一个二十面体，则它有12个顶点、30条棱以及20个面，这时12-30＋20=2。

对于这个定理，三角形是平坦的这一点并不重要∶我们可以把这些三角形画在原来的球面上，当然这样一来这些三角形都成了球面三角形。但是这样画了以后数它的顶点、棱和面还是一样容易，定理也仍然成立。画在球面上的这个三角形网格称为球面的三角剖分。

欧拉定理指出，不管对球面作什么样的三角剖分，总有V-E+F=2。此外，如果我们作了三角剖分的曲面并非球面，而是一个拓扑上与球面等价的另一个曲面，这个公式也是对的，因为三角剖分可以连续形变而V，E，F不会改变。

更一般地说，我们可以对任意曲面作三角剖分，然后估算V-E＋F，结果称为这个曲面的欧拉示性数。为使这个定义有意义，需要下面的事实，它是欧拉定理的推广，

虽然曲面可以用多种方法作三角剖分，量V-E＋F对所有的三角剖分都一样。

如果对曲面作连续变形，同时也对三角剖分作连续变形，就可以得出新曲面和老曲面的欧拉示性数一样。换句话说，事实（1）有下面有趣的推论∶

如果两个曲面互为连续形变，则它们有相同的欧拉示性数。

这一点给出了证明曲面不等价的潜在可能的方法∶如果它们有不同的欧拉示性数，它们就不会互为连续形变。环面的欧拉示性数为0（可以任作一个三角剖分，然后就能算出它的V-E＋F），因为这个结果与球面的欧拉示性数为2不一样，所以就知道球面和环面不会等价。

欧拉示性数是所谓不变式的一个例子。不变式就是一个函数 ，其域是我们所研究的那一类全部对象的集合，而且具有如下的性质∶如果两个对象 X 和 Y 等价，则

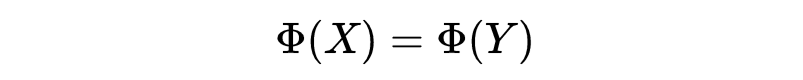
为了证明 X 和Y不等价，只需找到一个不变式使得

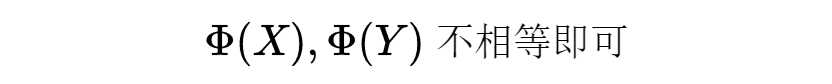
有时是一个数（欧拉示性数就是这样），但它们时常也可以是更复杂的数学结构，例如多项式或群。

一个极端的例子是，对于一切对象 X 都恒等于零的Φ ，它当然也是一个不变式。然而，有时证明对象不等价是如此困难，以至于不变式尽管只能部分情况有用，也认为不变式是有用而且有趣的。

对于一个不变式Φ，我们时常寻求它的两种主要性质，而这两种性质又时常是向两个相反方向起作用的。其一是要它尽可能的细，意思是，只要X和Y不等价，

其二是要能够实际地确定何时Φ（X）和Φ（Y）不同。一个不变式哪怕是很细，如果无法算出来，那就没有大用处。

一个极端的例子是"平凡的”不变式，即映一个对象入自己的等价类这样的不变式。它确实细到了极点。如果X和Y不等价，它们当然不在同一个等价类中，因此Φ（X）自然和 Φ（Y）不同，但是除非有独立的方法确定这个不变式，即找出这个对象的等价类，那么它对于原来提出的证明两个对象不等价这个问题，并不是一个进展。

所以，最强有力的不变式大概会是那些既能够计算出来，又不太容易计算出来的不变式。

在紧的可定向曲面的情况下，我们是运气很好的∶欧拉示性数不仅是容易计算的不变式，又确实能把所有的紧的可定向曲面作完全的分类。说准确一点，一个数k 是欧拉示性数，当且仅当存在一个非负整数g使得k=2-2g（所以可能的欧拉示性数只能是2，0，-2，-4，…，（相应于g=0，1，2，…）。具有相同欧拉示性数的紧的可定向曲面必是等价的，而数g就完全地确定了这个曲面。它称为曲面的亏格（genus），而可以几何地解释为曲面所具有的“洞”的个数（所以球面的亏格为0，环面的亏格为1）。