
问题
设k是一个正整数,设S是奇数素数的有限集合。证明最多有一种方法(旋转和翻折后重合的算一种)将S的元素放置在圆上,使得任意两个相邻元素的乘积对于某个正整数x的形式为x^2+ x + k。
这是2022年国际数学奥林匹克竞赛(IMO)第一天的最后一道题,也是第一天3道题中最难的一道。
69%的参与者在这个问题上得到0分(满分7分)。只有不到5%的参与者获得了全部7分。考虑到每个IMO参与者都是来自各个国家的前6的高中数学家之一,这道题的难度可想而知。

问题陈述很简短,相对容易理解。在深入研究之前,我们先从一个简单的问题入手。
圆中的3质数研究
考虑S包含3个质数。现在,不考虑旋转和反射,将任意3个数字排列到一个圆中只有一种方法。尽管如此,3个质数的情况仍然包含了许多对这个问题至关重要的见解。
下图显示了3个奇数素数集合S:{3,5,7},{3,5,11}和{3,5,13}。
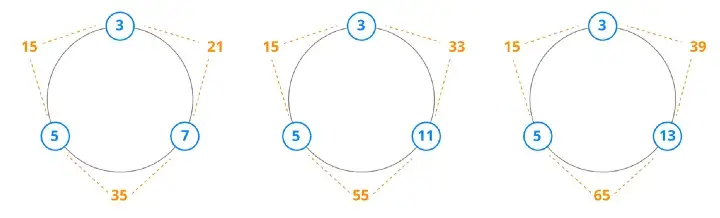
奇素数(蓝色)及其乘积(橙色)
上面的3个例子包含最小的奇素数3和5。这很容易研究,因为乘积15的形式是x^2+ x + k对于某个正整数x,只有几种情况:
x = 1,k = 13
x = 2,k = 9
x = 3,k = 3
x的任何较大值都使得x^2+x>15,那么k为负(但k是正整数)。
从集合S ={3,5,7}开始,我们想找出当k = 13, k = 9或k = 3时,剩下的乘积21和35是否可以表示为x^2+x+k。
绘制一个小表格来检验所有的可能性,我们发现没有一个k值适用于集合S ={3,5,7}
顺便说一句,如果允许x = 0,那么k = 15就可以。
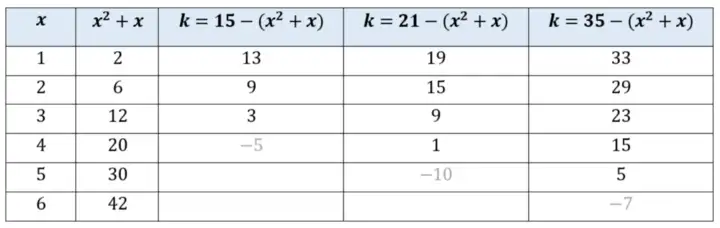
但是对于集合S ={3,5,11},我们发现k = 13就可以了。所有3个乘积15、33、55都可以表示为x^2+x+13。
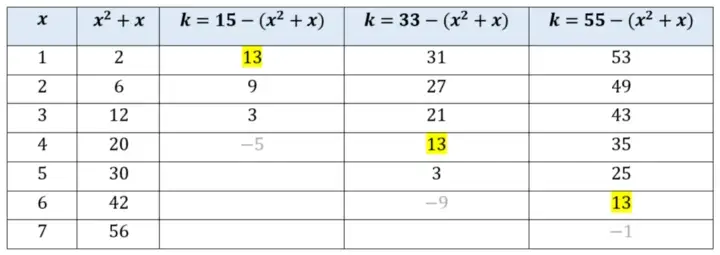
对于集合S ={3,5,13},所有3个乘积15,39和65都可以表示为x^2+ x + 9。
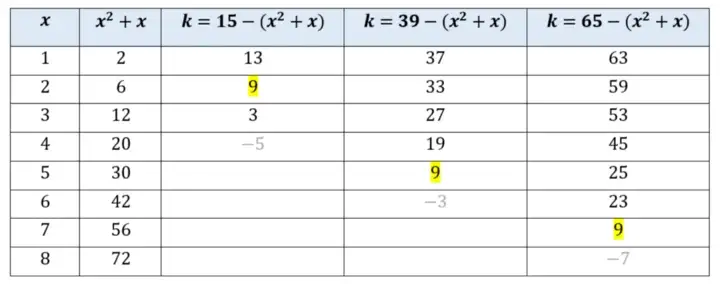
这似乎很令人惊讶,因为右边两列的唯一共同数字也是第一列的3个数字之一。
我想尝试一组3个略大的质数:S ={5,13,23},它们的两两乘积分别是65、115和299。
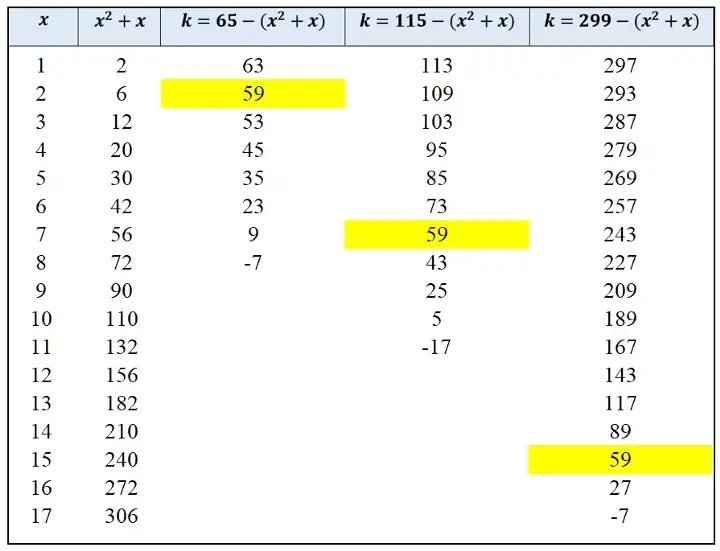
同样,有一个唯一的k值使得所有3个乘积都可以表示为x^2+x+k。可以发现,
最大的质数(23)总是比最大的两个x(15和7)的和大1,并且
两个最大的x值之差等于两个较小的质数之差。
例如,在上面的表中,对于S ={5,13,23},最大的两个x值是7和15。我们可以看到7+15+1 = 23,15−7 = 13−5。
这些观察结果使我们能够证明k对3素数集合的唯一性,并用数学归纳法来证明任何集合S的唯一性。
数学归纳法的证明
这个想法是为了证明对于有(n+1)个素数的集合S的任何合适的排列,去除最大的素数p给出了一个适合(且唯一的)n个素数集合的排列。另外,只有一对质数q, r可以放在p的旁边。加上3个质数的基本情况,这足以保证S的排列必须是唯一的。

我们将证明如果pq和pr都可以表示为x^+x+k,那么可以得出qr也一定可以表示为x^2+x+k(对于相同的k)。
设p为3质数中最大的,不是一般性的,p>q>r。
我们可以令pq = a^2+ a+ k,pr = b^2+ b+ k。
然后是减法:
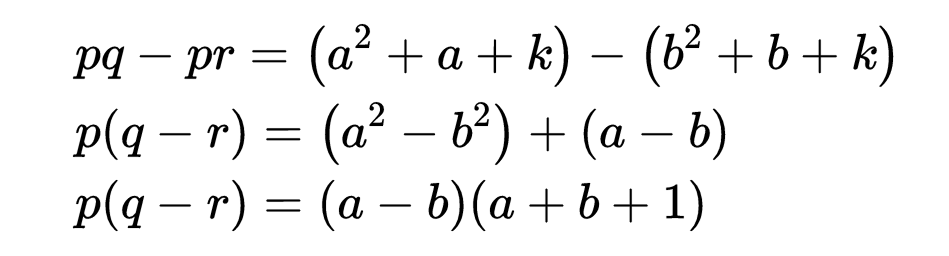
所以(a - b)或(a + b + 1)必须能被质数p整除,但因为a和b都小于p,所以它不可能是(a - b)。
另外,因为a + b + 1 < 2p,不仅(a + b + 1)能被p整除,而且它必须相等,所以p = a + b + 1。
现在要证明qr也必须有x^2+x+k的形式。
因为p(q - r) = (a - b) (a + b + 1)和p = a + b + 1,所以

重新排列得
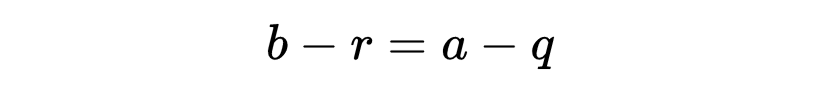
设这个公约差为d:
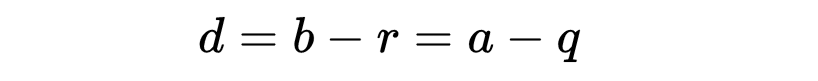
那么
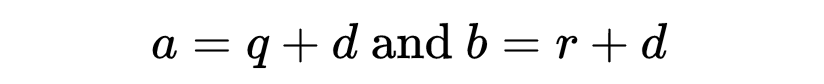
注意,a和b对于给定的q和r是固定的,这意味着它们是唯一的,因此k是唯一的。
又:p = a + b + 1,
因此:p = q + r + 2d + 1
将这些表达式代入方程pq = a^2+ a+ k,得到

得证,就这么简单。
评论列表