微分几何中, 曲面的第二基本形式(second fundamental form)是三维欧几里得空间中一个光滑曲面的切丛上一个二次形式,通常记作 II。与第一基本形式一起,他们可定义曲面的外部不变量,主曲率。更一般地,若在黎曼流形中一个光滑超曲面上选取了一个光滑单位法向量场,则可定义这样一个二形式。
要理解曲面的第二基本形式,先给出泰勒展开式:

再通过空间曲面的切平面给出ru、rv的方向如下:

下图是空间曲线的极坐标形式:


图1
上图通过泰勒展开式给出了PQ长度的近似计算方法。
在欧氏空间中,曲面的弯曲程度由曲面的第二基本形式刻画,其具体含义为曲面的第二基本形式Ⅱ近似地等于曲面与切平面的有向距离的两倍。
为了给出说明,给出下图:(参考B站一位老师的讲解)

曲面上点P'到切平面的垂直距离为P'Q,可以写为:
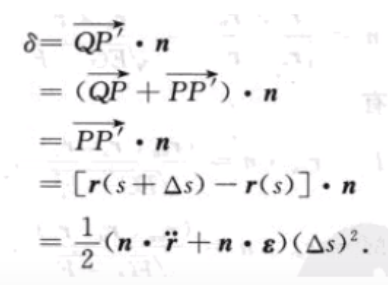
上图是与图1对比后得到,因为r'(t0)即表示切线PQ,处于切平面内,而n.r'(t0)=0。

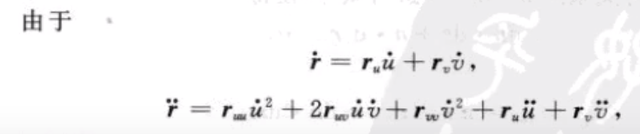


引进符号
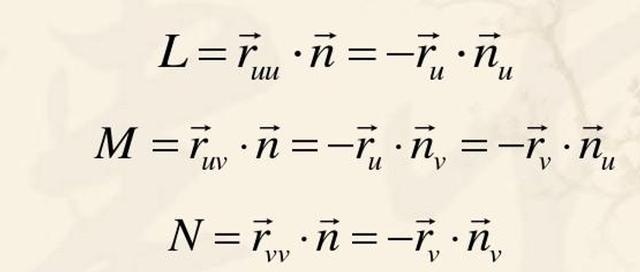
由此得到曲面的第二基本形式:


