任何数学分支，不管多么抽象，有朝一日都要应用于真实世界的现象。

蒙日学派

一切数学分支当中，几何学最容易受到不同时代之间不断改变的口味的影响。在古典希腊，它攀上了最高峰，不料大约在罗马衰亡的那一时期跌落至谷底。在阿拉伯和文艺复兴时期的欧洲，它收复了一些失地；在17世纪，它站在了一个新时代的门槛上，不料差不多又被遗忘了将近两个世纪，至少是被搞研究的数学家所遗忘，在不断增加的分析学分支的阴影里凋敝枯萎。英国，尤其是整个18世纪后期，试图把欧几里得的《几何原本》恢复到它曾经的光荣位置上，但英国在这一学科的研究上几乎没有取得多少进步。

通过蒙日和卡诺的努力，纯几何在法国大革命时期有了一些复活的迹象，但几何学作为一个活的数学分支，其几乎是爆炸性的重新发现主要是随着19世纪的黎明而出现的。蒙日在高等理工学院的学生对这次几何学的新发展做出了重要贡献。反映了他们老师的研究的多样性，一些学生追求几何学对工程学的应用，有的人从事教学，还有人致力于几何学对物理学的应用；很多人是为了几何学本身而研究这门学科。

夏尔·迪潘最为人们所铭记的是他对曲面理论的贡献，在这一领域，他提出了诸如四次圆纹曲面等概念，那是由所有与一组球体相切的球体所围成曲面。西奥多·奥利维尔在创造几何模型以发展几何概念的可视化上比蒙日走得更远；这项工作开始了几何模型收藏的积累，到世纪末，通过费利克斯·克莱因的教学影响，得到了极大的促进。夏尔·朱尔斯·布里昂雄今天因为一个定理而最为人们所知，他重新确立了人们遗忘已久的帕斯卡尔定理，布里昂雄用现代的形式把这个定理表述为：

在任何内接于一条圆锥曲线的六边形中，相对边的三个交点始终在一条直线上。

他继续通过另外一些证明，得出了一个被冠以他的名字的定理：

任何外切于一条圆锥曲线的六边形的三条对角线相交于同一点。

帕斯卡尔和布里昂雄的定理是几何学中一对重要的“对偶”定理最早的明确实例，也就是说，如果把“点”和“线”这两个词互换，定理依然有效（在平面几何中）。如果我们把“一条直线与一条圆锥曲线相切”读作“一条直线在一条圆锥曲线上”，则这两个定理可以表述在下面的组合形式中：

圆锥曲线上的点与线之间的这种关系，后来被另一位理工学院的校友有效地加以利用，此人后来成了射影几何的实际奠基者。他就是让-维克多·蓬斯莱，也曾受教于蒙日的门下。

射影几何：蓬斯莱与沙勒

蓬斯莱身陷囹圄期间，写了一本论述解析几何的专著《分析在几何中的应用》，尽管它最初是打算作为他另一部更为著名的作品、1822年出版的《论图形的射影属性》的导论。后一部作品明显不同于前一部，因为就风格而言，它是综合的，而不是分析的。后来，他成了综合方法的忠实倡导者。他认识到，解析几何似乎拥有的优势就在于它的一般性，因此，他试图在综合几何中作出尽可能一般化的陈述。他为了促进这一计划，构想出了他所说的“连续性原理”，或“数学关系的持久性原理”。他把这一原理描述如下：

针对原始图形而发现的度量性质，对于所有被认为是源自于最初图形的相关图形都依然适用，除了符号改变之外，无需其他的修改。

作为这一原则的一个例证，蓬斯莱引用了一个圆内相交弦的线段乘积相等的定理，当交点在圆外的时候，这个定理成了割线线段乘积相等。如果其中一条线是圆的切线，定理依然有效，只要用切线的平方取代割线线段的乘积。在某种意义上，这个原则跟卡诺的观点并无不同，但蓬斯莱把它带到了更远，包括开普勒和德扎格曾经暗示过的无穷远点。因此可以说，两条直线必定会相交———要么相交于一个平常的点，要么（在平行线的情况下）相交于无穷远处的一点，称之为理想点。为了实现分析的一般性，蓬斯莱发现有必要在综合几何中不仅引入理想点，而且还要引入虚点，因为只有这样你才可以说，一个圆和一条直线必定相交。在他的惊人发现当中包括这样一条：在一个平面上画出的所有圆都有两个交点，被称作无穷远处的虚圆点，通常被表示为I和J。

蓬斯莱认为，他的连续性原理———大概是从解析几何那里得到的暗示———完全是综合几何的一次发展。在18世纪下半叶，围绕解析法和综合法的优缺点，一直存在争论，尤其是在德国。1759年，数学家兼历史学家、莱比锡和哥廷根大学的教授A.G.凯斯特纳认为，解析法在用试探法解决问题的时候高出一筹，提供了思考的力量，比较省事。

19世纪几何学的历史充斥着独立发现和重新发现的实例。另一个牵涉到蓬斯莱的例子是九点圆的发现。蓬斯莱与布里昂雄在热尔岗的1820~1821年的《年刊》上联合发表了一篇论文，尽管它的题目是“直角双曲线确定的研究”，但其中包含了下面这个出色定理的证明：

从任意三角形的定点向它们的对边作垂直线，通过垂足的圆既通过各边的中点，也通过连接顶点与垂直线相交点所得线段的中点。

这个定理通常既没有被称作蓬斯莱定理，也没有被称作布里昂雄定理，而是用一个独立的德国数学家的名字来命名，他就是卡尔·威廉·费尔巴哈，他在1822年发表了这一结果。这篇短小的论文既包括了这个定理以及一些相关命题，也包括圆的几个引人入胜的属性的证明。其中包括这样一个事实：九点圆的圆心在欧拉线上，而且是垂心与外心之间的中点；以及“费尔巴哈定理”：任意三角形的九点圆内切于内接圆，并外切于三个旁切圆。美国几何学家朱利安·洛厄尔·柯立芝，把这个定理称作“初等几何中自欧几里得时代以来人们所发现的最优美的定理。”

应该指出的是，在整个19世纪，这样一些定理的魅力在很大程度上支撑了三角形和圆的几何学研究。除了雅各·施泰纳之外，这一领域最有名的贡献者大概是英国—美国几何学家弗兰克·莫利了。以莫利的名字命名的定理是这样：一个三角形各角的相邻三等分线的交点所构成的三角形是等边三角形。

回到蓬斯莱，我们之所以记得他，主要是因为他使用现有的德扎格的中心投影和无穷远点的概念来建立复射影平面的概念。基础是射影性质的研究，比如那些在透视下依然保持不变的属性。给定平面上的一个点O和一条直线l，一个透视赋给每个点P以直线l上的一点P'，使得：若Q是第二点，则OQ必定存在一点Q'，使得PQ与P'Q'在l上相交。一连串的透视被称作直射。蓬斯莱再一次求助于德扎格使用过的方法，使阿波罗尼奥斯的极点和极线的概念走上了前台，正如我们已经指出的那样，他把自己的对偶原理归功于极点和极线的概念。

米歇尔·沙勒在射影几何中强调了6个交比（或称非调和比），4个共线点或4条共点线的（c-a）/（c-b）∶（d-a）/（d-b），以及这些比在射影变换下的不变性。他的《论高等几何》在确立有向线段在纯几何中的使用上也很有影响。沙勒的《几何学中的方法的起源与发展简史》也很有名，他是法国最伟大的射影几何学家之一。他在晚年开创了枚举几何学的研究，这是代数几何学的一个分支，其任务就是要借助几何解释来确定代数问题的解法的数量。在这个领域以及其他领域，他极其出色地利用了“对应原理”。

综合度量几何学：施泰纳

沙勒的成果在很多方面与几个德国几何学家的成果相重叠。其中最著名的是雅各·施泰纳，他一直被认为是现时代最伟大的综合几何学家。在他的手上，综合几何取得的进展比得上早些年分析学所取得的进展。他非常不喜欢解析的方法。解析这个词暗示了一定数量的技术或机械；解析法常常被称作一个工具，而工具这个说法从未应用于综合法。施泰纳反对几何学中一切种类的工具或“小道具”。他只用综合的方法来论证，在发表于《克列尔杂志》上的一篇论文中，有一个引人注目的定理看上去自然属于分析学：一个三次曲面只包含27条线。

施泰纳还证明了，只要给你一个固定的圆，欧几里得的作图可以只用直尺来作。这个定理表明，在欧几里得的几何中，你不可能完全没有圆规，但是在用圆规画一个圆之后，你就可以丢掉圆规，只用直尺

施泰纳的名字在很多方面被人们所记忆，包括施泰纳点的属性：如果你用所有可能的方式把一条圆锥曲线上的6个点连成帕斯卡尔的神秘六边形，你就获得了60条帕斯卡尔线，三条三条地相交于20个施泰纳点。在施泰纳未发表的发现当中，有一些发现涉及到那种富有成果的被称作“反演几何”的几何变换：

若两个点P和P'在一条射线上，这条射线源自一个半径为r（r≠0）的圆C的圆心O，且OP和OP'这两个距离的积是r2，则我们就说，P和P'互为关于C的反演点。对圆外的每个点P，圆内都有一个对应的反演点。由于当点P与圆心O重合时圆外不存在点P'与P对应，于是我们就有了一个悖论，它在某种意义上类似于波尔查诺的悖论：每个圆（不管它多么小）的内部所包含的点，可以说比圆外部分还要多一个点。我们用完全一样的方式，很容易在三维空间里定义一个点关于一个球体的反演点。

很多平面或立体反演几何的定理，都很容易通过解析或综合的方法来证明。特别是，我们很容易证明：在反演变换下，一个不通过反演中心的圆被变换为一个圆，而一个通过反演中心的圆被变换为一条不通过反演中心的直线（类似的结论对三维反演几何中的球体和平面也适用）。更难证明的是这样一个更重要的结论：反演是保角变换，也就是说，在反演几何中曲线之间的夹角得以保持。保角变换很不寻常，这一点可以从约瑟夫·刘维尔所证明的下面这个定理中清楚地看出：在空间里，唯一保角的变换是反演变换以及相似和全等变换。施泰纳没有发表他的关于反演的观念，反演变换被这个世纪的其他数学家几次重新发现，其中包括开尔文勋爵，1845年，他通过物理学得出了反演变换，并把它应用于静电学中的问题。

如果半径为a的反演圆的圆心O是一个笛卡尔坐标系的原点，那么点P（x，y）的反演点P'的坐标x'和y'被下面的公式给出：

这两个公式后来启发了路易吉·克雷莫纳，他研究更加一般化的变换x'=R1（x，y）、y'=R2（x，y），式中R1和R2是有理代数函数。这样的变换（反演变换只是其特例）被称作克雷莫纳变换，以纪念这个在1863年发表关于它们的介绍的人，他后来针对三维空间把它们进行了一般化。

综合非度量几何学：施陶特

施泰纳在他1832年出版的《几何图形之相互依赖性的系统发展》中论述了基于度量考量的射影几何。若干年后，纯几何学找到了另一位德国信徒，他就是高斯的学生K.G.C.冯·施陶特，他1847年出版的《位置几何学》构建了不涉及量或数的射影几何学。施陶特的几何学极其重要，因为它显示了射影几何如何能在没有距离概念的情况下建立起来，因此为下面这个观念铺平了道路：有一种非度量几何，可以在它的基础上定义距离概念。几年之后，法国的拉盖尔讨论了把度量强加给非度量角度几何学的可能性。然而，正是阿瑟·凯莱，后来在他的“六论齐次多项式”中，对于在射影几何的基础上定义度量的整个概念，提出了最有影响的阐述。

解析几何

现在我们转向解析几何在这一时期所取得的成就。正如蒙日大概是第一个专攻一般意义上的几何学的现代数学家，尤利乌斯·普吕克成了第一个专攻特殊意义上的解析几何的数学家。他坚定地相信，代数学方法大大优于蓬斯莱和施泰纳的纯几何方法。19世纪初，很多人都认识到了，解析几何被代数计算的笨拙所拖累；因此，他们开始大幅度地对符号进行缩略。1818年，加布里埃尔·拉梅把所有通过两个圆

的交点的圆族简单地写作：

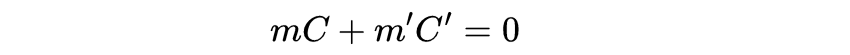
使用了两个参数或乘数m和m'。拉梅似乎是通过简记法来研究单参数族解析几何的创始者，但正是普吕克，把这项研究带到了最远。

普吕克还发现了一种新的坐标系，就是我们所说的齐次坐标，费尔巴哈是它的发明者之一。另一个发明者是A.F.莫比乌斯，他是这样提出了自己的“重心坐标”：考虑一个给定的三角形ABC，定义点P的坐标，使得当你把一个质点放在A、B和C上时，P是这些质点的重心。莫比乌斯对变换进行了分类，所依据的是全等、相似、仿射（对应图形保持平行线）和直射，并暗示了在每一个变换族下不变性的研究。然而，莫比乌斯之所以被人们记住，是因为“莫比乌斯带”。

齐次坐标是在几何算术化的方向上跨出的一大步，但在1829年，普吕克提出了一个革命性的观点，与笛卡尔把坐标视为线段的古老观点彻底决裂。齐次坐标系中一条直线的方程具有这样的形式：

三个参数系数（a，b，c）决定了平面上的唯一一条直线，正如齐次坐标（x，y，t）对应于平面上的唯一一点一样。由于这些坐标是数，因此跟系数并无不同，普吕克认识到，可以修改通常的语言，把齐次坐标（a，b，c）称作一条直线。最后，如果把笛卡尔的惯例颠倒过来，用字母表中开头的字母代表变量，用末尾的字母代表常量，则方程ax+by+ct=0就代表了一束通过固定点（x，y，t）的直线，而不是固定直线（a，b，c）上的一束点。现在，如果你考虑意义不明确的方程pu+qv+rw=0，则有一点很清楚：你可以毫不在乎地把这个方程视为固定直线（p，q，r）上的点（u，v，w）的总和，或者视为通过固定点（u，v，w）的直线（p，q，r）的总和。

普吕克发现了几何学对偶原理的分析学等价物；现在，有一点已经很清楚：纯几何曾经徒然寻找的理由在这里已由代数学的观点提供。“点”和“直线”这两个词的互换，只不过相当于关于量p、q、r和u、v、w的“常量”和“变量”这两个词的互换而已。从代数位置的对称性来看，很显然，关于pu+qv+rw=0的每一个定理都直接以两种形式出现，互为对偶。

此外，普吕克还证明了，每一条曲线（不同于直线）都可以被视为有双重来源：它是一条由一个移动的点所产生的轨迹并被一条移动的直线所包围，该点不断沿着该直线移动，同时该直线继续围绕该点旋转。说来也怪，在点坐标中一条曲线的次数（曲线的“阶”）未必跟线坐标中曲线的次数（曲线的“类”）一样，而且，普吕克的伟大成就之一是4个用他的名字命名的方程的发现，把曲线的类和阶与曲线的奇点联系起来了：

式中m是类，n是阶，δ是节点数，κ是歧点数，ι是平稳切线（拐点）数，τ是双切线数。从这些方程一眼就可以看出：一条圆锥曲线（或二阶曲线）可以没有奇点，因此必定也是二类曲线。

在1831年，普吕克把对偶原理扩展到了三维，在三维空间里，一个平面的齐次坐标（a，b，c，d）与一个点的齐次坐标（x，y，z，t）之间的关系表明，三维空间里一个定理的对偶定理是通过“点”和“平面”这两个词的互换而得到的，“直线”这个词保持不变。在后来的论文和专著中，普吕克把他的工作扩展到包括笛卡尔虚坐标系和齐次虚坐标系。现在，证明蓬斯莱定理（所有圆都相交于无穷远处的两个虚点）就是小事一桩了，因为，点（1，i，0）和（i，1，0）都满足方程

不管a、b、c取什么值。普吕克还证明，圆锥曲线的焦点有这样一个属性：从这些焦点到曲线的虚切线通过上述圆的交点；因此，他把高次平面曲线的焦点定义为一个有这一属性的点。

在笛卡尔和费马的时代，以及在蒙日和拉格朗日的时代，法国都是解析几何发展的中心，但因为普吕克的工作，这一领域的领袖地位便跨过了莱茵河，转移到了德国。然而，普吕克在很大程度上是一个在本国没有获得什么荣誉的先知。在德国，综合方法的捍卫者施泰纳受到了过度的赞美。莫比乌斯在解析—综合论战中一直保持中立，但雅可比，尽管本人是一个运算法则的构建者，却加入了施泰纳的阵营，反对普吕克。灰心丧气的普吕克在1847年从几何学转向了物理学，在这一领域，他发表了一连串论述磁学和光谱学的论文。

我们惊讶地注意到，普吕克并没有利用行列式的发展，这大概是因为他与雅可比之间的长期不和；这或许就是他为什么没有系统地发展三维以上解析几何的原因。普吕克通过他在1846年的观察接近了这个观念：决定三维空间中一条直线的4个参数可以被认为是4个坐标；但只是多年之后，也就是在1865年，他才回到了解析几何，并发展出了“新的空间几何”的观念———即四维空间，其中基本元素是直线，而不是点。与此同时，柯西在1843年开创了n维空间的普通解析几何，使用行列式作为基本工具。在这种符号表示法中，使用齐次坐标，直线和平面的方程分别可以写作

凯莱曾指出，n维空间中对应的（n-1）维基本元素可以通过一个n+1阶行列式用齐次坐标来表示，类似于上面的两个行列式。很多二维和三维的简单公式，如果得到恰当的表示的话，都很容易一般化至n维。

黎曼几何

几十年来，非欧几何一直是数学的一个边缘方面，直到它通过波恩哈德·黎曼非常一般化的观点彻底整合起来。黎曼以一篇论述有一个复变量的函数理论的论文获得了博士学位。正是在这一领域，我们有了所谓的柯西—黎曼方程：

有一个复变量z=x+iy的解析函数w=f（z）=u+iv必定满足这两个方程，虽说这个必要条件甚至早在欧拉和达朗贝尔的年代就已经被人所知。这篇博士论文还导致了黎曼曲面的概念，预示了拓扑在分析学中最终要扮演的角色。

1854年，黎曼成了哥廷根大学的编外讲师（没有薪水），按照老规矩，要求他在全体教师面前宣讲一篇授课资格论文，结果是数学史上最著名的一次试讲，因为它呈现了一次对整个几何学领域深刻而闳阔的概览。这篇论文的标题是《论奠定几何学基础的假设》，但它并没有拿出一个明确的实例。相反，它极力主张一种几何学的全局观，作为任何种类的空间里任意维度的流形研究。他的几何学跟罗巴切夫斯基的几何学比起来，是更加一般意义上的非欧几何，在前者那里，问题仅仅是有多少条可能的平行线通过一点。黎曼认识到，几何学甚至大可不必处理平常意义上的点、直线或平面，而是要处理依据某些规则组合而成的一组组有序的n元组。

黎曼认识到，在任何几何学中，最重要的法则，是求出无穷靠近的两个点之间的距离的法则。普通的欧氏几何中，这个“度量”被：

给出；但有无数多的其他公式可以用作距离公式，而使用的度量当然会决定空间或几何的属性。一个空间，如果度量是下面的形式：

式中g是常量，或者更一般的情况下，是x、y和z的函数，则这个空间就被称作黎曼空间。

因此（局部说来），欧氏空间只不过是黎曼空间的一个非常特殊的特例，在欧氏空间里，

而其他的g全都等于零。黎曼甚至得出了一个公式，用来求他的“空间”里一个“曲面”的高斯曲率。在黎曼的讲课之后，高斯几乎是平生头一遭对别人的工作表现出热心。

我们今天是在一个更加有限的意义上使用黎曼几何这个术语：它是一种从萨凯里的钝角假设推导出来的平面几何（如果抛开直线的无穷性）。这种几何的一个模型，可以从下面这样的解释中找到：它把“平面”解释为一个球体的表面，把“直线”解释为球体上的一个大圆。在这种情况下，一个三角形的各角之和大于两个直角。正是黎曼提出弯曲度量空间的一般研究，而不是相当于球面几何的特例，最终使得广义相对论成为可能。黎曼本人在很多方面对理论物理做出过重大贡献，因此，1859年，他被任命为狄利克雷的继任者，执掌哥廷根大学那个高斯曾充任过的教席，是再合适不过的。

黎曼在证明三角形各角之和大于两个直角的非欧几何是在球面上实现的过程中，本质上证明了几何学赖以产生的那些公理的一致性

高维空间

黎曼所实现的几何学的统一在不同几何的微观方面（“局部”几何）尤其重要。解析几何（“全局”几何）没有什么大的改变。1868年，普吕克发表了一篇论文，论述“新的空间几何”。他在这篇论文中，明确地阐述了他大约在20年前暗示过的一个原理。他认为，大可不必把一个空间想象为点的总和；同样可以把它想象为由直线组成的。事实上，任何一个从前被想象为点的轨迹或总和的图形，本身都可以被当作一个空间的构成元素来对待，空间的维度相当于决定这个元素的参数的数量。如果我们把平常的三维空间看作是一个“由无限细、无限长的稻草所堆成的宇宙稻草堆”，而不是一个“由无限细小的铅弹所构成的凝聚块”，它就是四维空间，而不是三维空间。凯莱从分析学上发展出了这样一个观念：普通的二维平面可以被视为一个五维空间，它的构成元素是圆锥曲线。

费利克斯·克莱因

克莱因在某种意义上是普吕克的继任者，然而，他采取了不同的方向，这个方向有助于把某种统一的元素带入新研究成果的多样性中。新观点部分程度上或许是探访巴黎的结果，在那里，拉格朗日关于群论的暗示已经发展成了———尤其是通过置换群———代数学的一个成熟的分支。克莱因对群概念中的统一可能性留下了深刻的印象，他把余生的全部时间都花在了发展、应用和推广这个概念上。在这项工作中，他与挪威数学家索菲斯·李携手合作，李发现了切变换，并写了一部厚重的三卷本论著，论述变换群理论。李的切变换（后来被克莱因系统化了）以这样一种方式在欧氏空间的直线与球体之间建立一一对应的关系，使得相交线对应于切球。（按照克莱因的观点，欧氏三维空间里的直线和球体各自构成了一个四维空间。）一般而言，切变换是把切曲面带入切曲面的解析变换。

一组元素如果符合下面这些条件，我们就说它们构成了关于某个给定运算的一个群：（1）这组元素在该运算下是封闭的，

（2）这组元素包含一个关于该运算的单位元素，

（3）对于组中的每个元素，都有一个关于该运算的逆元素，

（4）该运算是结合运算。

元素可以是数（比如在算术群中）、点（在几何群中）、变换（在代数群或几何群中）或者任何东西。运算可以是算术运算（比如加法或乘法）或几何运算（比如围绕一个点或一根轴旋转），或任何其他把组中的两个元素（比如两个变换）结合起来构成组中的第三个元素的运算法则。群概念的概括性很明显。1872年，克莱因成为埃尔朗根大学的教授时，在一项著名的就职纲领中显示，群如何能够作为一个很方便的手段，用来描述19世纪所出现的各种不同的几何的特征。

克莱因拿出的这项纲领（后来被称作“埃尔朗根纲领”）把几何学描述为研究那些在某个特定变换群之下依然保持不变的图形的性质。因此，对变换群的任何一种分类都成了几何学的一种规范化。例如，欧氏平面几何所研究的是这样一些图形的属性（包括面积和长度），它们在由平面上的平移和旋转（所谓的刚性变换）所组成的变换群之下依然保持不变，相当于欧几里得未曾说出的公理：这些图形在一个平面上移动的时候依然保持不变。从分析学的角度讲，刚性平面变换可以写作下面的形式：

式中，ae-bd=1；这些构成了一个群的元素。把这样两个元素“结合”起来的“运算”只不过是按顺序变换而已。不难看出，如果在上面的变换之后紧接着执行下面的变换：

连续两个运算的结果，等价于这种类型的某一单个运算，它将把点（x，y）带到点（x″，y″）的位置上。

在这个变换群中，如果用更一般的条件：ae-bd≠0，取代原先的条件：ae-bd=1，则新的变换也组成了一个群。然而，长度和面积未必保持不变，但一条给定类型的圆锥曲线（椭圆、抛物线或双曲线）在这些变换下将依然是同一种类型的圆锥曲线。这样的变换，莫比乌斯更早研究过，被称作仿射变换，它们是所谓的仿射几何的典型特征，之所以这样称呼，是因为在这样的变换下一个有限点变换为一个有限点。那么很显然，从克莱因的观点来看，欧氏几何只不过是仿射变换的一个特例。反过来，仿射几何也只不过是一种更加一般的几何———射影几何———的一个特例。射影变换可以写作下面的形式：

很显然，如果d=0=e，且f=1，这个变换就是仿射变换。射影变换的有趣属性包括：

（1）一条圆锥曲线被转变为一条圆锥曲线，

（2）交比依然保持不变。

在某种意义上，克莱因的工作是“几何学的英雄时代”的一个当之无愧的高潮，因为他讲课和教学的时间长达半个世纪。他的热情具有极强的感染力，以至于19世纪晚期的一些重要人物都很乐意支持群论最终不仅把几何学包括在内，而且把数学的所有分支都纳入其中。今天，他的名字还在那个被称作“克莱因瓶”的单侧曲面的拓扑中被人们所铭记。

后黎曼时代的代数几何

到19世纪末，有几种新方法研究几何学，通常按照代数几何的不同版本来分类。在黎曼的作品中有一个共同的基础。不是黎曼的明确属于几何学的出版物，而是他的论述复变函数理论的作品，尤其是跟一篇论述阿贝尔函数的经典论文中黎曼曲面的概念相关联的作品，为大多数这样的研究提供了促进因素。

起初，阿尔弗雷德·克莱布什在为了几何目的而利用黎曼的函数理论上所做的工作比其他任何人都要多。克莱布什最早在一篇题为《论阿贝尔函数对几何学的应用》中对这一课题给予了关注。这是一次三重方向进攻的开始。克莱布什最初只是着手把黎曼的复变函数理论应用于代数曲线的研究。他有充分的能力来完成这项任务；他熟悉复射影几何学家们先前的工作，熟悉阿贝尔函数理论的雅可比传统，熟悉黎曼的论文。他获得了很多卓有成效的成果，为进一步的研究奠定了基础。

另一种方法，在克莱布什与埃尔朗根大学的戈尔丹合作完成的作品中使用。在1866年出版的著作《阿贝尔函数理论》中，他们着手在代数几何的基础上重建阿贝尔函数理论。戈尔丹作为19世纪不变量理论的捍卫者而被人们所铭记，在这一背景下我们注意到世纪之交的意大利几何学派，包括卡斯特尔诺沃、恩里克斯以及稍晚的塞韦里，都十分看重不变量理论。

最后，克莱布什转向了曲面研究。他提出了二重积分，希望通过探索与阿贝尔积分应用于曲线研究的类似方法来获得结果。

最活跃的方向是把双有理变换应用于曲线研究；很多数学家都注意到，黎曼的模只不过是双有理不变量，从而用黎曼的术语来表述他们的研究。尽管欧洲主要中心的数学家们做了大量的工作，但最终的结果似乎令人失望。到1920年代，大多数这样的“代数几何学”努力开始退居次要位置，让位于纯代数方法，这一方法在一般性和抽象性上日益提高，在代数几何学中处于支配地位长达几十年。