拓扑空间中的闭包定义如下:

由以上定义可以看到,闭包因为是所有闭集的交,所以其结果还是一个闭集。


这里的
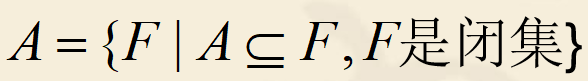
意思就是,如果A是一个闭集,则A等于包含它的那个最小闭集,其实就是等于自身。
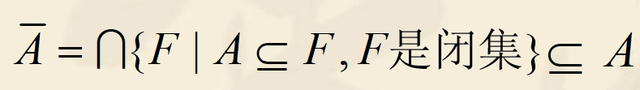
这一步的意思是,任意两个以上集合的交集,必然包含于其中任意一个集合。
闭集A等于包含A的最小闭集
结论:在拓扑空间中,闭集A等于包含A的所有闭集之交,也即是最小的包含A的闭集。
关键信息梳理:
闭集定义:闭集是指其补集为开集的集合。
包含关系:若B是包含A的闭集,则A⊆B。

由以上证明可以看到,按照闭包的定义,闭包一定是一个闭集。
对于一个闭集A来说,因为包含这个闭集A的闭包包括这个闭集A本身,而闭包又是一个最小的闭集,那这个最小的闭集当然是集合A本身,所以对于闭集A来说,等于它的闭包就是当然的结果。

