我们知道f ' (x) = f(x)形式的微分方程的解是指数函数f(x) = Ce^x。因为f ' (x) = C(e^x) ' = Ce^x = f(x)。但如果我们不知道这个公式，怎么能从零开始推导出来呢？我将展示这个推导过程的七个步骤。

第一步：

我们重写函数f(x)求y = f(x)。为了明确我们对什么函数求导，在这种情况下，y是x的函数，我们对x求导。

我们可以把微分方程f ' (x) = f(x)写成dy/dx = y

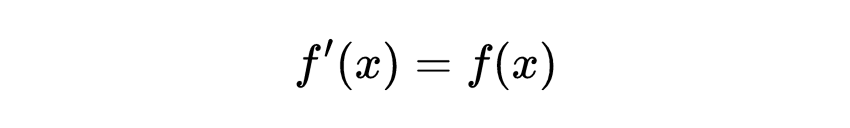
重写为

我们的目标是找到满足dy/dx = y的函数。

第二步

有一种可能是y是常数函数，y = C，例如，y = 1, y =−100，等等。

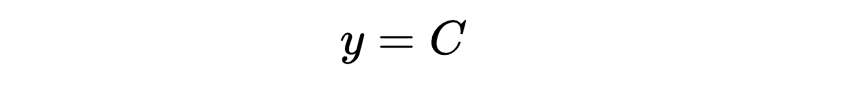
两边同时微分x。

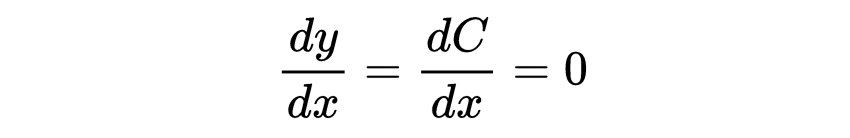
为了满足dy/dx = y，y必须是y = 0。

因此，y = 0是微分方程dy/dx = y的一个解。

第三步：

从现在开始，我们将关注y≠0的情况。微分方程两边除以dy/dx = y（y≠ 0）

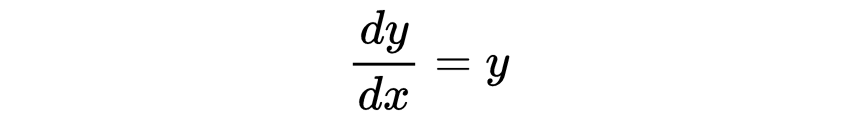
第四步：

两边关于x积分。

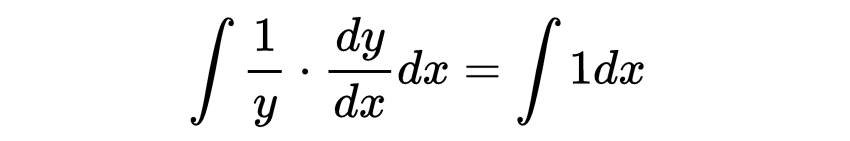
右边的积分很简单。C_1是一个积分常数。

第五步：

你可以用代换积分法对左边积分。

一般来说，1/y的积分是这样的。

因此，方程的左边是这样的。C是一个积分常数。

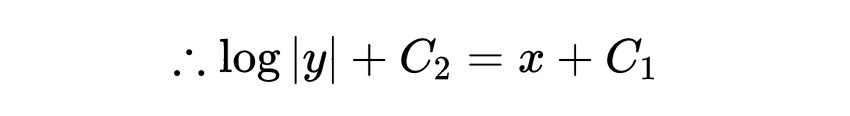
把C_2移到右边。

让C_3为 C_3= C_1−C_2，得到

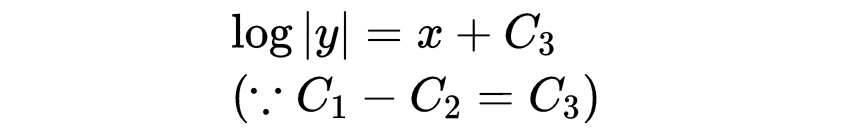
第六步：

由于

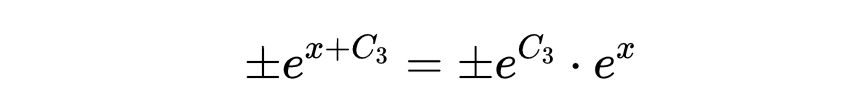
而±e^C_3是一个常量，所以可以用另一个常数C≠0重写，因为±e^C_3≠0。

得到y = C 'e ^x

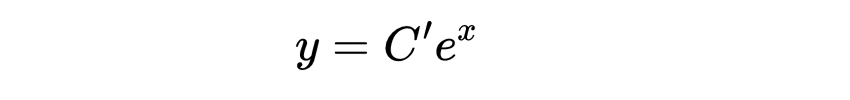
第七步：

从上面的讨论中，我们似乎得到了两种不同的解：

虽然在C '≠0的情况下，y = C ' ^x不等于y = 0。但是，如果我们用C '替换另一个任意常数C，它可以是C = 0，y = C ' ^x就是y = Ce^x。当C = 0时，y = Ce^x = y = 0。

通解y = Ce^x包含特解y = 0。因此，我们可以得出微分方程f ' (x) = f(x)的解是f(x) = Ce^x （C是任意常数）。