数学史上级数出现得很早，在两千多年前人们就有了粗糙的级数思想。古希腊时期，亚里士多德就知道公比小于1（大于零）的几何级数可以求出和数。芝诺的二分法涉及到把1分解成无穷级：

阿基米德在《抛物线图形求积法》一书中，使用几何级数去求抛物线弓形面积，并且得出了级数：

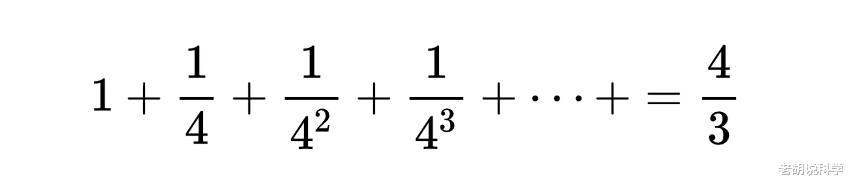
中国古代《庄子·天 下》中的“一尺之捶，日取其半，万世不竭”含有极限的思想，用数学形式表达出 来也是无穷级数。

到了中世纪，由于数学家和哲学家对一些涉及到无穷思想的悖论展开了激烈的争论，使得关于无穷级数的研究开展起来。最具代表的是法国数学家奥雷姆用最初等的方法证明了调和级数：

是发散的，用现在的形式可表示为：

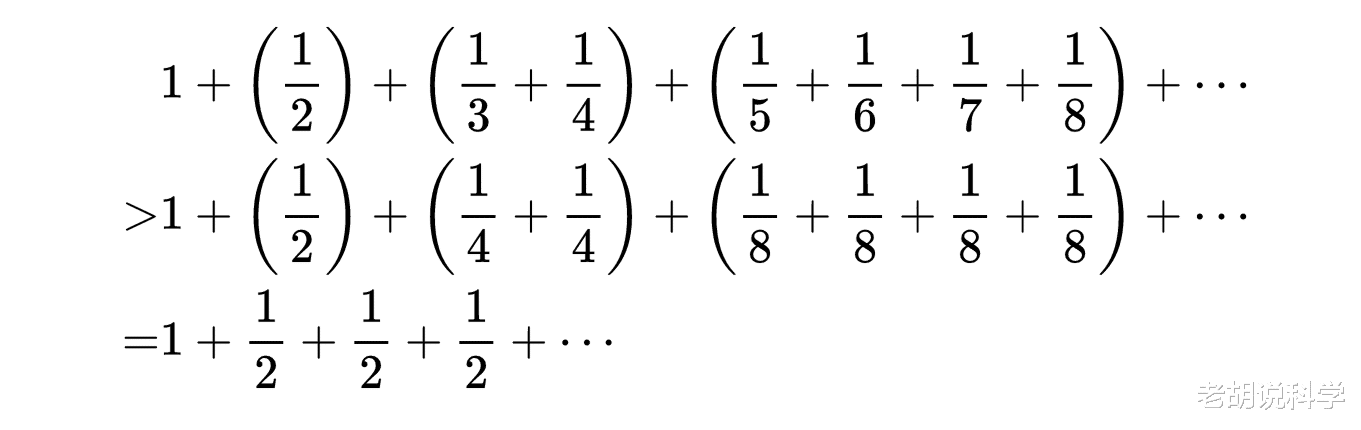
中世纪的级数理论，从本质上看没有突破性进展，它的主要贡献并不在于所得到的具体结果，而是在于促使人们接受一种新的观点，即在数学中可以自由的承认无限过程。这对后来理解无穷过程做了铺垫，为形式化处理级数奠定了思想基础。

早期数学家仅凭直觉就认为级数是可以收敛的，并将级数从有限项自然地拓展为无限项使用，这导致了有限法则无限拓展的产生。17世纪，伴随着微积分的产生，许多数学家通过微积分的基本运算与级数运算的形式化结合，得到了一些初等函数的幂级数展开式，并且级数在解析运算中被普遍用来代表函数而成为微积分的有力工具，这就使得无穷级数成为微积分不可缺少的部分。

1669年，牛顿在他的《用无限多项方程的分析学》中，用级数反演法给出了sinx，cosx的幂级数，arcsinx，arctanx和e^x的级数展开。格雷戈里得到了tanx，secx等函数的级数，莱布尼茨也在1673年独立地得到了sinx，cosx和arctanx等函数的无穷级数展开式，以及圆面积和双曲线面积的具体展开式。在微积分的早期研究中，有些函数如指数函数等超越函数的处理相当困难，然而人们发现，若用它们的级数来处理，则非常有成效。因此，无穷级数从一开始就是莱布尼茨、牛顿等人微积分工作的一个重要部分。有时使用无穷级数是为了计算一些特殊的量，如π和e以及求隐函数的显式解。

17世纪后期和18世纪，为了适应航海、天文学和地理学的发展，摆在数学家们面前的问题之一是函数表的插值。由于对函数表的精确度要求较高，数学家们开始寻求较好的插值方法，牛顿和格雷戈里给出了著名的内插公式：

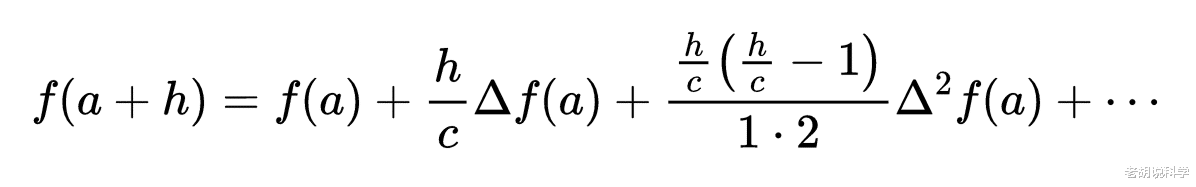
1715年泰勒发表了《增量方法及其逆》，奠定了有限差分法的基础。17世纪，牛顿、莱布尼茨等人曾研究过有限差分问题，泰勒的工作则使有限差分法从局限的方法（如二项式定理、有理函数的长除法、待定系数法等等）过渡到了一般的方法。这本书中他给出了单变量幂级数展开的著名公式，即泰勒级数：

泰勒是第一个发表此级数的人，但他不是第一个发现此级数的数学家。在他之前格雷戈里、牛顿、莱布尼茨、约翰·伯努利和棣莫弗等数学家都研究过此级数。例1717年泰勒运用这个级数求解方程，取得了很好的结果，但是他的证明是不严格的而且没有考虑收敛问题，在当时影响并不太大。直到1755年，欧拉在微分学中将泰勒级数推广

应用到多元函数，增大了泰勒级数的影响力，随后拉格朗日用带余项的泰勒级数作为函数论的基础，才正式确立了泰勒级数的重要性。后来麦克劳林重新得到泰勒公式在口=0时的特殊情况，现代微积分教材中一直将这一特殊情形的泰勒级数称为“麦克劳林级数”。

詹姆斯伯努利与约翰伯努利在级数方面做了大量的工作。詹姆斯伯努利在1689到1704年间撰写了5篇关于无穷级数的论文，成为当时这一领域的权威，这些论文的主题是关于函数的级数表示及其求函数的微分与积分，求曲线下面积和曲线长等方面的应用，所有这些级数的应用是对微积分的重大贡献。

随着级数理论的发展，原始的级数思想已经不能解释一些级数，例如渐近级数，循环级数，连分数等等。这使得许多数学家们采用更加形式化的方法来解决级数的问题，欧拉就是其中一位。欧拉的工作非常广泛，他把无穷级数由一般的运算工具转变为一个重要的研究科目，使得无穷级数的应用和发展到了另一个高度，为后来无穷级数理论的发展奠定了坚实的基础，并为我们展示了许多精妙的思想，留下了深刻的启示。下面从几个方面讨论欧拉的级数思想。

欧拉对级数收敛和发散的认识

形式化观点在18世纪无穷级数的工作中占统治地位，级数被看成是无穷的多项式，并且被当作多项式来处理，对其收敛和发散的问题没有深入研究。欧拉多少意识到收敛性的重要，他也看到了关于发散级数的某些困难，特别是用它们进行计算时产生的困难。欧拉将收敛级数定义为，“级数的项不断地减小，当级数的项数趋于无穷时，它的项完全消失，这样的级数被称为收敛级数”“发散级数则就是那些不是收敛级数的级数，即级数项为某个不为零的有限量或趋于无穷的级数。在级数理论研究中，欧拉还运用了一个原则：若级数的部分和是无穷小的，则级数是收敛的。这个原则看起来像柯西准则的非标准版，但却是以一种现代的方式来发现收敛级数与发散级数的差别。欧拉关于收敛级数的定义是不能令人满意的，欧拉也认识到这一点。因为欧拉曾研究过一些级数，级数的项越来越接近于，但和却趋于无穷，如调和级数，欧拉关于这类级数也进行了研究。

调和级数

在18世纪，伴随着级数理论不断发展，各种初等函数的级数展开陆续得到，并在解析运算中被普遍用来代表函数而成为微积分的有力工具。但对于级数理论本身而言，其中最具启发性的工作是关于调和级数和为无穷的证明。调和级数的讨论引起了学者们对发散级数的兴趣并产生了许多重要的结果。

欧拉研究了调和级数：

并能够用对数函数求调和级数的有限项地和。

欧拉是从

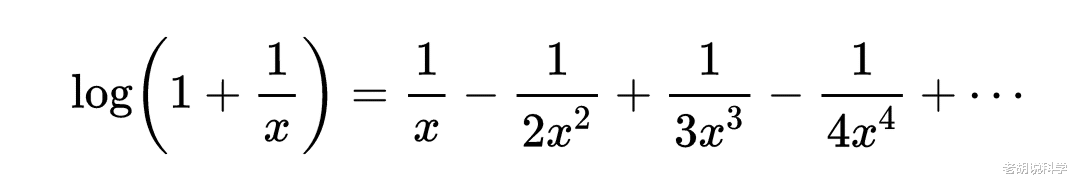
出发，于是

带入x=1,2,3，……n就得出

各式相加，并注意到每一个对数项是两个对数之差，就得到：

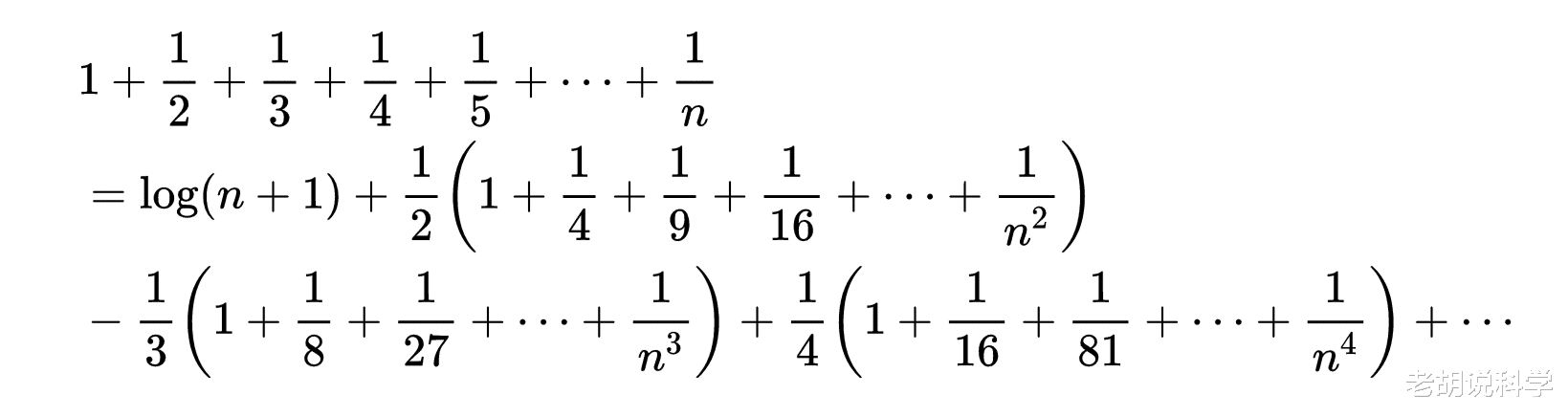
或

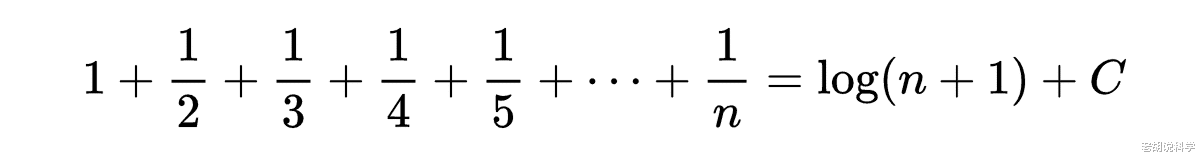
其中C表示无穷多个有限算术的和，欧拉近似的计算过C的值，并得到C=0．57721566490153286060651209……这个C现在通称的欧拉常数，用γ（gamma）表示。这是继π、e之后的又一个重要的数。γ的一个更精确的表示，今天是如下得到的。

上式中，两边减去logn得到：

当n一∞时它趋于0。

因此

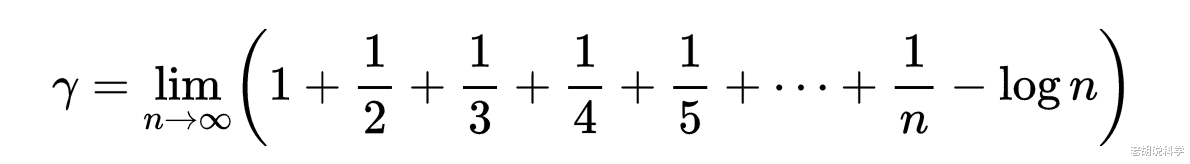
得到了这个关于y的最简单的表达形式，到目前为止，关于γ的性质还没有弄清楚（是否是代数数，是否是超越数）。

欧拉常数——最神秘的数字，调和级数的产物，至今看不清它的面貌​

巴塞尔问题

欧拉在数学领域获得的第一个令人注目的成绩就是在1735年解决了巴赛尔问题。巴赛尔问题是指求整数倒数的平方和问题，即：

巴赛尔问题是由法国数学家门戈利在1644年提出的，后来这个问题被雅各布伯努利于1689收录在一本名为《没有结论的无穷级数》的书中，并引起了数学家们的广泛关注。

许多数学家都进行过探讨，虽然大家试图考察这类级数的收敛性，但都没有给出级数和的精确值，均以失败告终，其中包括奥雷姆、莱布尼茨、彼得罗·门戈利、雅各布伯努利和约翰伯努利。

1731年，24岁的欧拉从他的老师约翰．f白努利那里听说了这个难题，经过一年的反复研究，发现了解开这个谜的钥匙，他兴奋的写道：

…完全意想不到，我发现了基于π的一个绝妙公式。

欧拉一共用四种不同的方法来解决巴赛尔问题，最著名的是第三种方法。

欧拉解决这个难题的两个重要环节是：利用正弦函数的泰勒展开，把正弦函数表达为无穷多项式；研究一般的代数有限多项式的性质，将其推广应用到无穷多项式，即将其形式化处理。

首先欧拉给出一个玎阶多项式p(x)，这个多项式满足有n个非零根a1,a2,a3,…，an。且p(0)=1，即有：

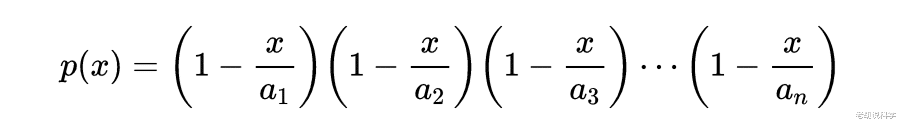
欧拉令：

再将正弦函数sinx进行泰勒展开得到：

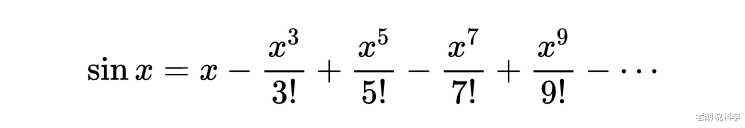
则得到：

当x≠0时，

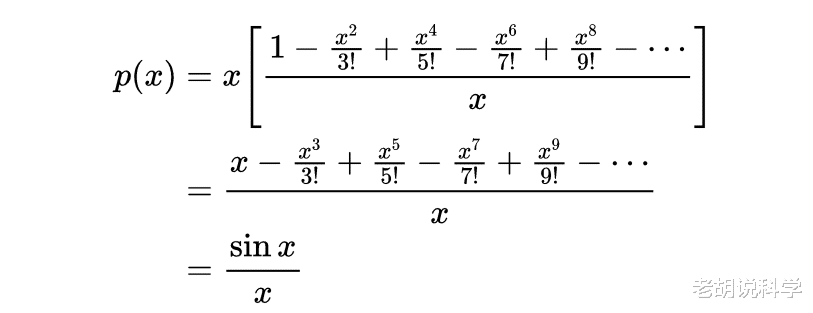
所以p(x)=0(x≠0)的解等价于sinx=0的解，为x=±kπ，k=1，2，…

则：

即有：

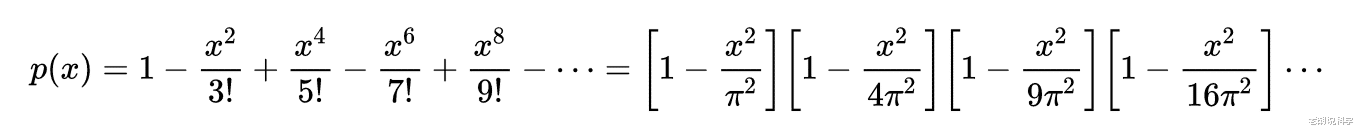
成立。欧拉得到的这个等式非常重要，是解决这个问题的关键。接着，欧拉将这个等式的右端展开，得到：

再根据系数相等，得到

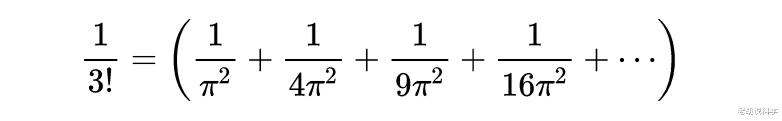
即

在这个过程中，很明显能够看出欧拉处理级数的形式化方案，通过这两个重要环节相结合使用，欧拉发现了其他数学家几十年未能发现的结论。

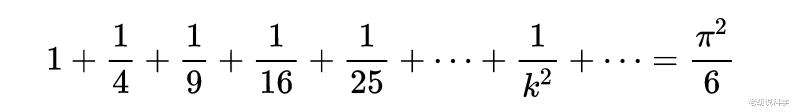
欧拉的工作非常重要，特别是关于整数乘方倒数与万之间的巧妙关系，是人类认识的一大进步。