提问：假如未来，人类遇到了必须这么做的情况下，且不惜一切代价，运用一切科技解决了面临的所有问题，建成了这个可以正常使用的超级望远镜，假如地球依然正常运转，人类有可能“望”穿宇宙吗？能否洞悉宇宙的奥秘？

答案是——

不行。

射电望远镜精度比光学望远镜低多了，足足低了2000~2000万倍。

即便是地球大小的射电望远镜，能看清一个人的最远距离也仅仅只有110万公里，仅相当于地球轨道半径的1/135，月球轨道的3倍。

你要“看穿”可观测宇宙，只要求看清太阳直径那么大的范围，都需要3000万倍地球大小的射电望远镜。

看清地球直径的范围，则足足需要33亿倍地球大小，相当于4.5光年。

要在宇宙边缘看清楚一个人，则需要用450个银河系来打造这个超级射电望远镜。

若要看清0.5mm的圆珠笔芯，需要把我们整个可观测宇宙，做成一个超级射电望远镜。

以下是分析和计算过程：

望远镜的分辨率，由瑞利判据所决定。

很多人应该都有这样的经验，当用不同形状的小孔对着光源，把光斑照射在墙壁上，孔越小，光斑的形状也就越模糊。

如果点变得更小，就会形成明暗相间的光斑，这便是爱里斑。

人在分辨足够小的物体时，本质上相当于分辨相邻的点光源。

两个过于靠近的点光源，会因为衍射图像互相重叠而不可分辨。

在光学中，把恰好能分辨的度数称为瑞利判据。

其公式为：

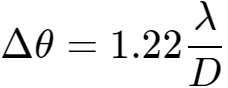
θ为角分辨度（这里的单位是弧度rad），λ为光线的波长，D为孔径大小。

由于角分辨度反应的是所能观察到的最小精度，因此越小越好。

系数 1.22 通过爱里斑第一个暗圆环的位置计算得出。

这个数字更准确地说是 1.21966989……它是通过第一类贝塞尔函数一阶计算而来。

这个公式告诉我们，光波长越短，孔径越大，才有越高的角分辨度。

瑞利判据公式适用于任何光学系统，当然包括我们的眼睛，光学望远镜，以及射电望远镜。

对于光学望远镜来说，由于可见光的平均波长为550nm。

天文望远镜中，一般用角秒表示。

1度=60角分=3600角秒，半圆周等于648000角秒。

1rad=180°/π=648000″/π

主镜直径用 L 表示，单位为厘米。

因此，把弧度转变成角秒则为：

考虑到观察时的主要可见光，可能存在一定范围变化，天文望远镜角分辨度的典型值为：

13/L~14/L

可以看出，天文望远镜的分辨率只和它的口径有关，这是因为口径越大所能收集的光越多，成像质量也就越好。放大倍数并不影响分辨率，但放大倍数上限被口径大小所限制。

对于一个口径200cm的天文望远镜来说，观察月球距离（38万公里），得到的分辨精度为：

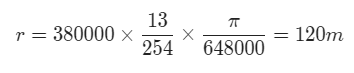
所以，人类用大型天文望远镜观察月球的时候，分辨精度通常在100~200m，最多只能看到山和陨石坑，网上流传的一些所谓外星人影像，一眼假的根本原因便在这里。

目前人类通过探测器到达月球轨道，也才仅仅能得到数米精度的影像，连个人影都看不清的。

要达到所谓望穿宇宙，你至少要达到1米的精度，才能大约看出个人影吧？

那么，地球这么大的光学望远镜（口径为12742km），看1米的精度，可以看到多远呢？

容易计算出，这个距离为

L=20217124661794m

也即20.2亿千米。

而日地平均距离1.496亿千米（1个天文单位），相当于13.5个天文单位。

土星轨道9个天文单位，天王星轨道19个天文单位。

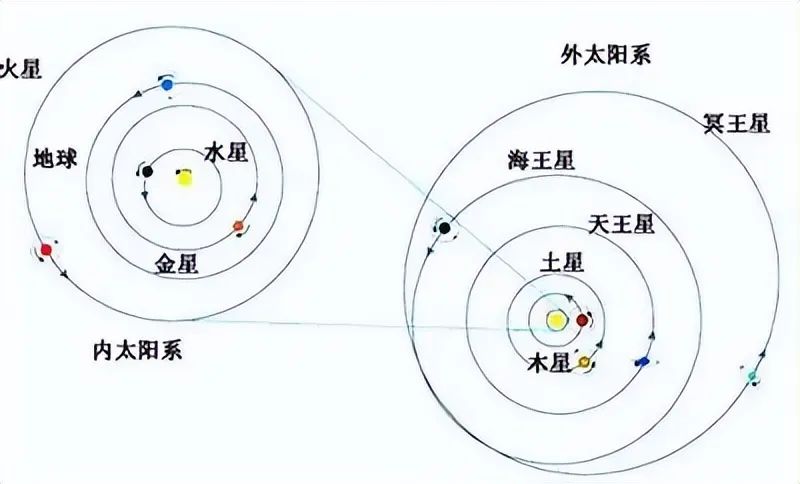
也就是说，地球这么大的光学天文望远镜，要看到1米精度，也仅仅只能看到土星和天王星之间。对于天文尺度来说，距离其实相当有限。

然而刚才讨论的仅仅是光学天文望远镜，对于射电望远镜来说，分辨精度还更低。

无论光学望远镜也好，射电望远镜也罢，它的原理本质上都是对光子进行收集成像。

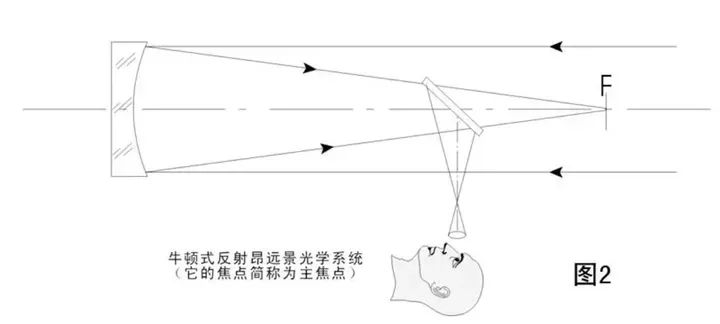
只不过光学望远镜所用的光是可见光范围，射电望远镜所用的光是无线电波范围。

射电望远镜所用波长范围通常为1mm~10m，最小波长也是可见光波长的2000倍左右。

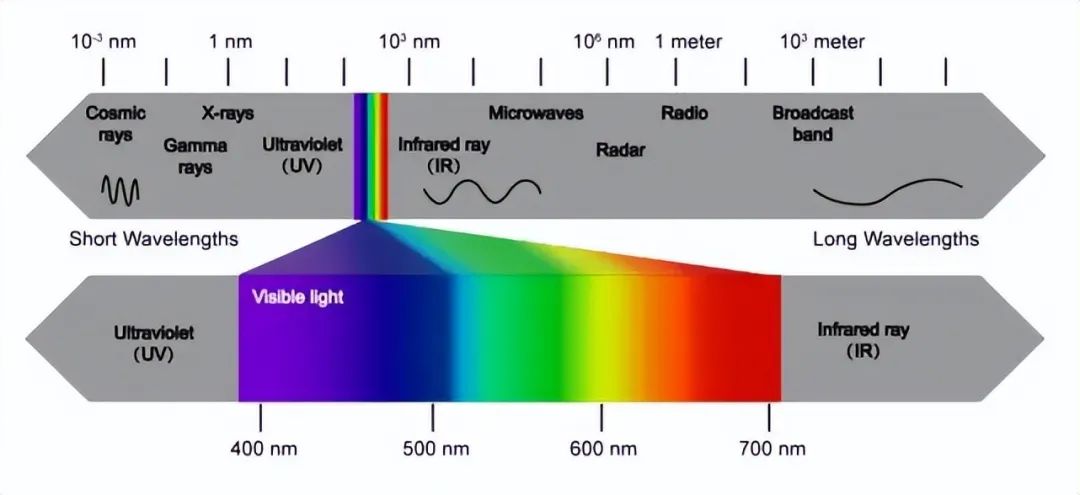
由于角分辨度的大小与波长成正比，因此要达到和光学望远镜相同的精度，射电望远镜口径就需要至少增大2000倍。

考虑到射电望远镜的不同用处，观察时需要不同电磁波，就注定了一些射电望远镜的精度比较低，最高需要口径增加2000万倍以上，才能相当于光学望远镜的精度。

氢原子占宇宙的90%以上，宇宙中分布中大量的星云，这些星云发射的电磁波频率1.4GHz，要“看穿”宇宙，不看这些星云完全过不去。这大约相当于0.21m波长的电磁波。也大约需要增加40万倍口径，才能相当于光学望远镜的精度。

单纯从数据上，我们就可以看出射电望远镜的精度有多低了！

最后我们再对比一下，射电望远镜的分辨率有多垃呢？

人的正常瞳孔直径，通常在2~4毫米左右，夜间会稍大一些，可以达到5~7mm。人眼角分辨度大约相当于哈勃（口径240cm）的1/500。然而人眼的角分辨度却相当于1.4GHz射电望远镜2000米口径。

世界最大射电望远镜中国天眼FAST，口径500米，在脉冲星观察上非常的牛，然而角分辨度仅仅只有人眼的1/4。（当然，这本身是光波长所限制，并不是说人眼牛或者FAST不行。如果人眼能看到1.4GHz电磁波，那反而只有FAST精度的10万分之一了。）

天眼的角分辨度并不高，重点在于看到人眼所不能。在宇宙起源、天体结构、极端环境物质规律的观察发挥着无比重要的作用。

单纯为了看得远的话，需要依赖的还是射电望远镜矩阵——甚长基线阵列（VLBA)。

所谓甚长基线阵列，就是修建多个射电望远镜，联合成一个巨型望远镜。

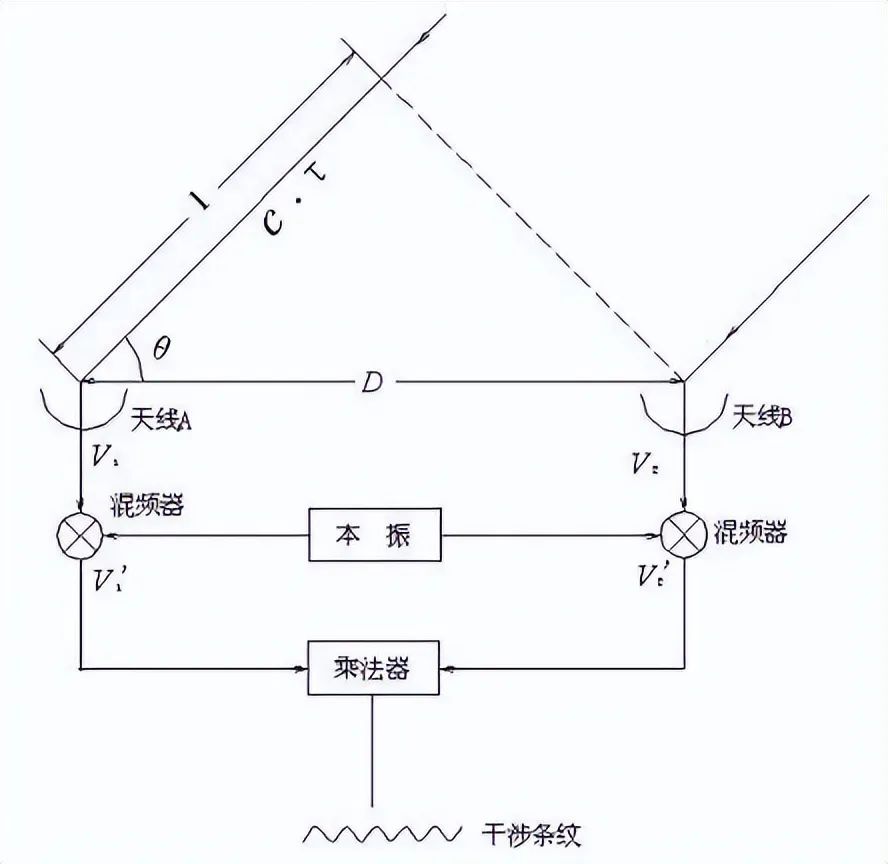
大尺度的甚长基线阵列，弥补了射电望远镜的精度劣势。虽然相同大小口径的精度仅仅只有光学望远镜的数万分之一，但建个10公里的阵列，就能媲美光学望远镜的精度。

如果把1000公里外的射电望远镜阵列再联合起来，构成更大的阵列，那么精度就可以超过光学望远镜的100倍以上。

射电望远镜阵列对于大领土国家来说，具有天然的优势。例如，美国的VLBA，横跨8000千米，精度达到哈勃的500倍，相当于人眼的60万倍。

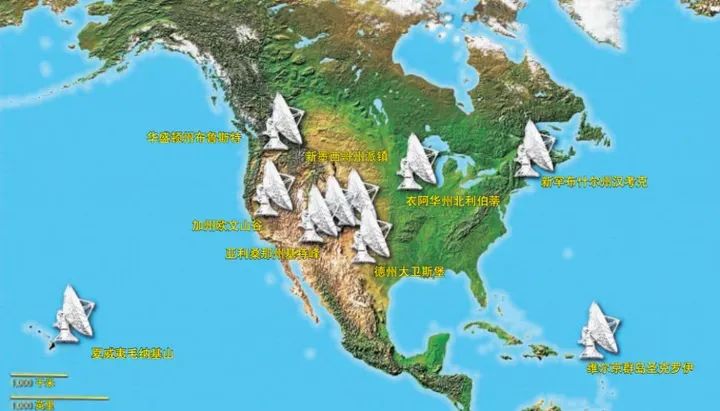
但我们也必须注意到，和地球级大小的光学望远镜相比，地球级大小的射电望远镜依旧具有数万倍的差距。

人类观察到的第一个黑洞的照片，5500万光年外的M87*黑洞，所用的便是遍布全球的8个毫米/亚毫米波射电望远镜。为了观察这个黑洞，科学家已经尽可能用了最高角分辨度的射电望远镜（电磁波）。

易得，观察这颗黑洞的射电阵列，角分辨度为：

∆θ=0.000000000096 rad

5500万光年的分辨尺度为：

r=5×10^10 km

也即500亿公里，相当于300多个天文单位。

M87*黑洞的质量高达65亿倍太阳质量，根据史瓦西半径公式：

可知质量为1.989×10^30 km的太阳，理论视界半径为2953m，M87*黑洞的视界半径为192亿万千米，约 2×10^10 km。

M87*黑洞的视界半径不到分辨精度的1/2，这也是为什么人类得到的首张黑洞照片会如此的“高斯模糊”。

容易计算出，这个地球大小的射电望远镜，要能看清楚一个人的距离大约是110万千米，非常接近太阳的直径，只有地球轨道半径的1/135，月球轨道的2倍，这比宇宙级别小得太多了。

精度要求低到地球直径，也只能看到1光年外，相当于太阳系外围大小。仅仅只是太阳系到M87*黑洞距离的1/5500万。

而整个可观测宇宙的半径是465亿光年，是太阳系与M87*黑洞距离的845.46倍。

即便我们认为题主所谓的“看穿”，仅仅只是500亿公里的低精度，都需要800多倍地球级大小的射电望远镜，相当于8个太阳大小。

如果精度提高，你需要看清可观测宇宙边缘史蒂文森2-18这种级别的恒星（2158倍太阳直径），需要的射电望远镜大小，则相当于130个太阳大小，略大于地日轨道距离（1天文单位）。

要看清太阳这种级别恒星（直径1.392×10^6 km），则需要3000万倍地球大小的射电望远镜，接近太阳的30万倍大小，2600个天文单位。相当于太阳日球层（狭义上的太阳系大小）大小的26倍。

要看清地球这种级别的星球，则需要33亿倍地球大小的射电望远镜，相当于28万个天文单位，约相当于4.5光年，相当于等于整个奥尔特云直径（广义上的整个太阳系大小）大小的2倍还多。

也已经足够囊括4.3光年外的半人马座α（比邻星）。

这意味着，人类和三体人合作，我们的射电望远镜和它们的射电望远镜联合，一起形成阵列，才能看到宇宙边缘地球这种级别的行星。

要看看清整个天安门广场，则需要5万光年大小的射电望远镜，相当于太阳绕银河系轨道的直径。

如果要看清一个人，需要4500万光年大小的射电望远镜，相当于银河系与仙女座的20倍距离，450个银河系，已经非常接近地球到M87*黑洞的距离。

如果你想要看清0.5mm的圆珠笔芯，则需要900亿光年大小的射电望远镜，几乎等于可观测宇宙的直径。

也就是说，哪怕仅仅对于整个可观测宇宙来说，在宇宙边缘，你即便设计出最大的射电望远镜，能看到的最高精度，也不会超过0.5mm。

然而，以上计算仅仅用的1mm的电磁波，如果用氢原子1.4GHz的0.21m波长电磁波，宇宙级大小的射电望远镜也仅仅只能看清一只猫。银河系大小的射电望远镜，能约莫看清北京城。如果囊括所有类型的射电望远镜，宇宙级也只能看清一栋小楼，银河级则只能看出中国轮廓。

实际上，宇宙中存在大量的星体活动，各种电磁干扰、射线干扰，还有星云遮挡，类星体遮挡。再加上不同物质发射出不同频率的电磁波……即便你真的制造出了宇宙级的射电望远镜，看整个宇宙也相当于走屏障林立的夜路，你拿着手中的蜡烛，不仅试图看穿整个黑夜，还意图看清楚所有的细节。

即便科技树对人类无限开放，打造宇宙级的望远镜，人类都无法做到看穿整个宇宙，更不用说地球级的射电望远镜了。