如果说,昨天关于拉普拉斯变换带给我们的数学知识太过抽象,没听懂也没关系,毕竟他还和我们的生活接触太过“疏远”了,我们表示先保持接触,不深交即可。
但是,今天这个秘密武器,你可要必须知道啊!
可以说,要是没有这个工具,什么机器人技术、控制系统、四轴飞行器等等虽不能说不存在,但肯定能说它们的系统会变的很不稳定,以至于无法“存活”。
你比如说,在处理传感器数据时它是非常重要的。机器人依赖各种传感器(如视觉、声学、激光等)来感知环境。而它能用于分析和过滤这些传感器信号,提取有用信息,去除噪声。
四轴飞行器的飞行稳定性依赖于精确的控制算法,它能保证分析飞行器稳定性等等。
哈哈,它就是“工程之王”—— 傅立叶变换!
先看下面这个动图,看能不能看懂。

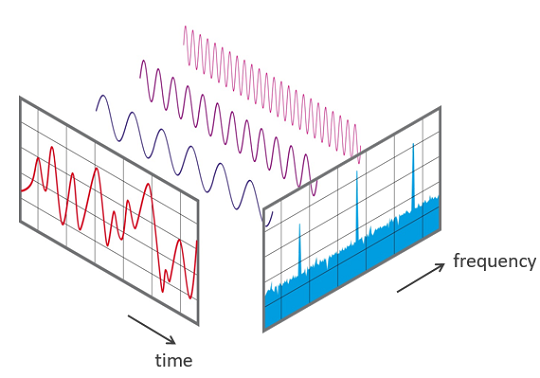
傅里叶变换将函数的时域(红色)与频域(蓝色)相关联。频谱中的不同成分频率在频域中以峰值形式表示。
好,接下来我们仔细谈谈。
01 小白认知傅立叶变换
傅里叶变换(Fourier Transform),这个在科技领域无处不在的数学工具,你可能已经在大学课程中接触过。
即使你没有正式学过,也许在科技新闻或某些科普读物中听过这个词。
傅里叶变换可以说是构建现代科技的基石之一,几乎渗透到我们的生活每个角落。
手机播放MP3音乐、图像处理、语音识别,这些日常应用无一不依赖傅里叶变换的强大功能。
那么,什么是傅里叶变换?为什么它如此重要?
从本质上来说,和昨天谈的拉普拉斯变换一样,其实傅里叶变换是一种将复杂事物拆解成简单事物的方法。
为了更直观地理解,我们可以以声音为例。
注意,声音只是傅里叶变换的一个应用例子,这种方法并不限于声音或波动。
众所周知,声音是空气的震动。当你拨动琴弦时,耳边传来的音调其实是空气以固定频率震动的结果。
例如,一个标准的A音符大约每秒震动440次。这个频率和震动的幅度决定了音调和音量。
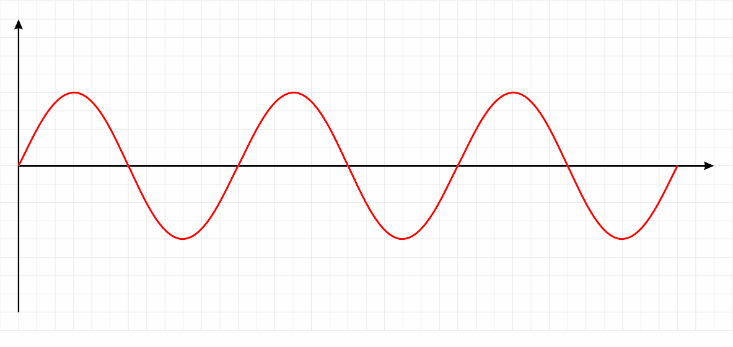
假如我们把简单的声音可以用如下图表示,横坐标是时间,纵坐标是震动的幅度。这个波形呈现出完美的周期性变化,说明它是一个单纯的音调,即正弦波。
然而,真实世界中的声音往往不是单一音调,而是复杂的震动。这种复杂的声音看起来杂乱无章,如下图所示:

复杂的声音
关键的洞见在于:复杂的震动可以看作是一系列简单震动的叠加。例如,上图中的复杂波形实际上是几个简单波动相加的结果,如下图所示:
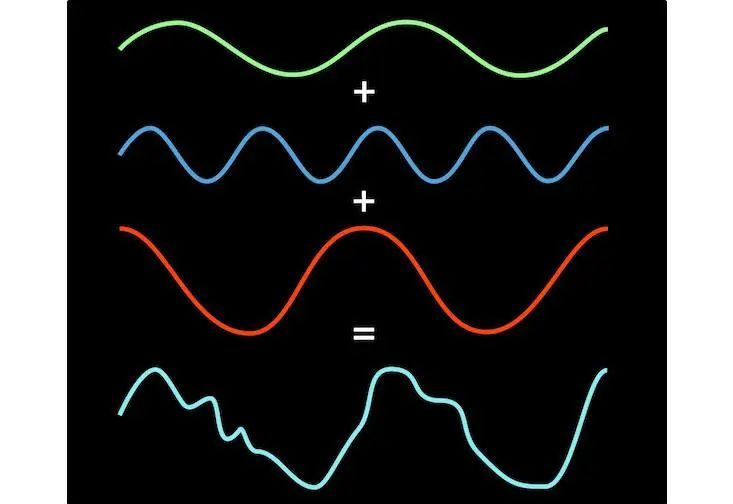
这就像一天中的温度变化,你可能感受到的温度变化非常复杂,但实际上你经历的是几种简单变化的叠加。红色曲线可以代表自然温度的变化,绿色曲线表示你是否在室内,蓝色曲线代表你是否穿上外套。
傅里叶变换就是在这个背景下运作的:如果我们先规定好一系列简单波动,那么任何一个复杂波动都可以用这些简单波动拆解。
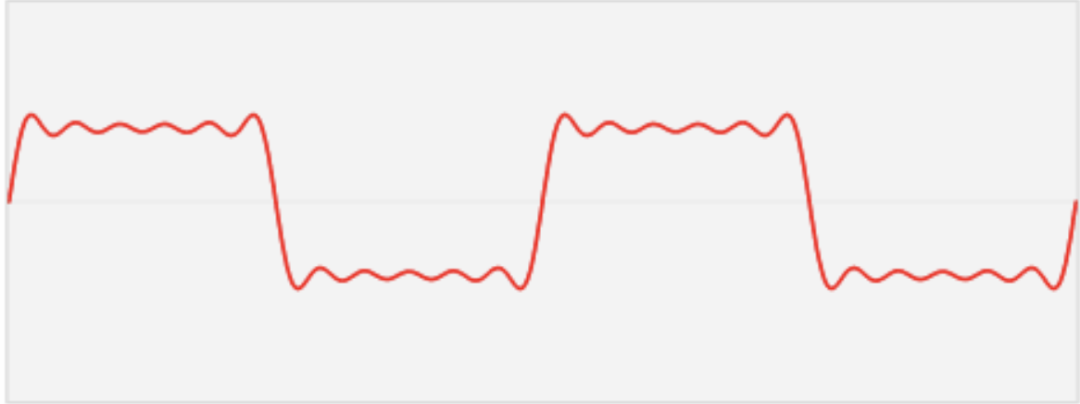
复杂波形
例如,上面这个波形看似复杂,但其实可以分解为几种简单波动的叠加:
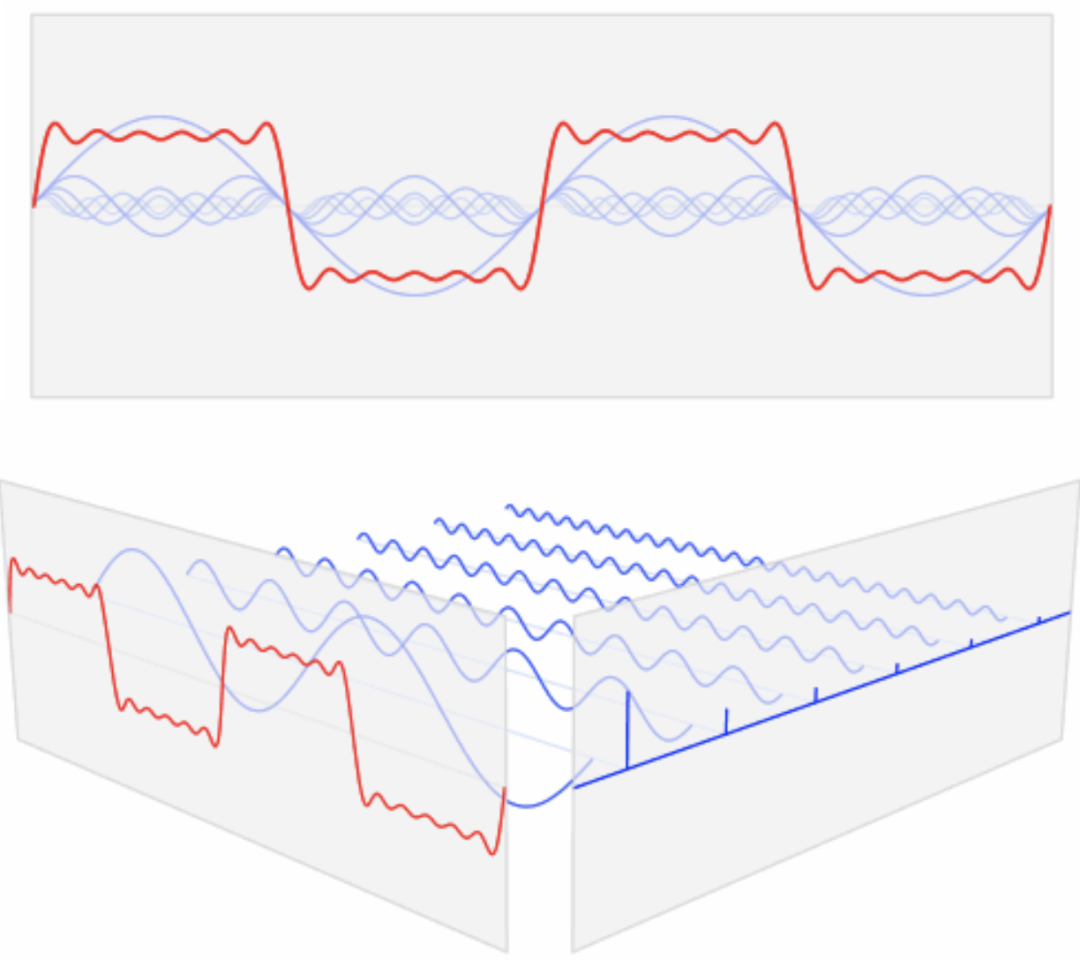
拆解之后的波形
上图中的蓝色曲线就是一系列简单波动,傅里叶变换能告诉我们每一个简单波动对复杂波形的贡献度。我们可以表示为:
红色曲线 = 频率是100的蓝色曲线 × 0.5 + 频率是200的蓝色曲线 × 0.2 + 频率是300的蓝色曲线 × 0.1 + 频率是400的蓝色曲线 × 0.08 + ……
如果这些蓝色曲线都是约定俗成的“标准化简单事物”,那么描绘复杂波形时只需要记录这些简单波动的“成分”即可——这就是傅里叶变换的基本原理。
现在你看出傅里叶变换的好处了吧?
02 傅立叶变换的应用
通过几个数字我们就可以描绘一条复杂的曲线,这也正是数字音乐的原理。
标准化的简单音调是大家约定好的,只需记录一个声音分解成简单音调的成分值即可。
因为特别高频和低频的声音人耳听不见,标准化简单音调数量是有限的,用很有限的数字就能描绘复杂声音,这就是WAVE音频格式的基本原理。
再进一步压缩处理,就成了MP3。类似地,JPG图像的原理也是通过傅里叶变换,把时间上的波动变成空间上的波动。
傅里叶变换不仅限于声音或图像,它可以应用于任何信号处理。
例如在工程领域,用来分析机械振动;
在医学中,用于处理脑电波;
在天文学中,用来分析星体信号等。
总之,傅里叶变换是一种强大的工具,能将复杂现象分解为简单的成分,从而简化分析和处理。
不过这里我不得不提下,我作为机器人制造厂商对“傅立叶变换”的应用——减速机异响分析。

一款RV工业机器人减速机
我们知道,减速机在工业机器人上有至关重要的作用,如提高关节扭矩、高精度、高负载等。
但,因为机器人长期运动会导致减速机发生异响或磨损。这个时候就需要我们就会采集减速机的数据(如位置误差、电流)等等,然后用傅立叶变换进行分析。
比如下图:
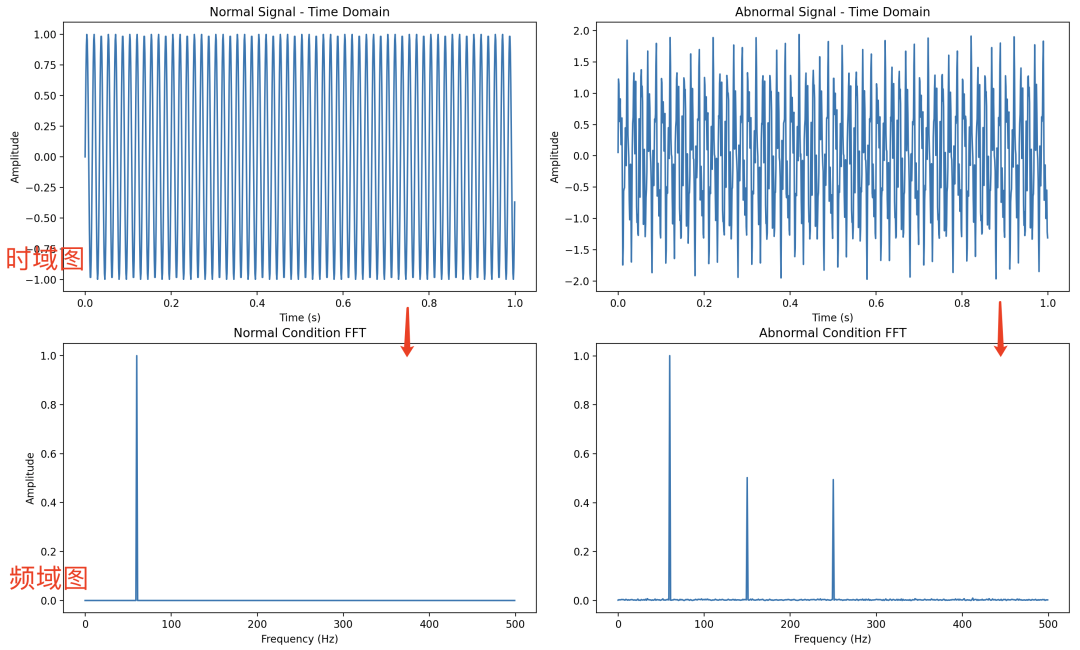
左边是正常减速机的数据对应傅立叶变换的数据分析,对应的频域图只有一个频率的噪音(当时这只是模拟数据,实际会比这个更复杂)
右边就是异常减速机的数据对应傅立叶变换的数据分析,可以看出多出了2个柱子,而2个多出的柱子就是噪音来源。
这个时候你就要去分析究竟是什么原因导致的。
而老师傅一般一眼看出可能是装备问题等等,因为频率的数据就代表了一种异常来源,见得多了,什么频率对应什么事件一般都是清楚的。
当然,傅里叶变换并不要求记录的信息具有周期性。任何形状的线条都可以用那些标准化的简单曲线合成出来,哪怕只有一个周期也是可以做的。
这些“标准化的简单音调”如何选取有一定讲究,要求“不重不漏”。
所谓不漏,就是组合在一起必须覆盖耳朵能听见的所有频率;不重,则是这些音调之间不能有重叠。
这些标准化的简单事物是傅里叶变换的基石,可以想象成“维度”。
复杂事物就像由这些简单事物构成的多维空间中的一点,每一种简单事物的成分构成了这个复杂事物的坐标。
为了保证坐标系统的清爽,各个维度之间应该是互相垂直(数学上叫“正交”)的关系。
03 生活中的傅立叶变换,我们是怎么实现的

你看,你每一次对着菜谱做菜,都是在进行一种傅里叶变换。
菜谱中用到的食材、盐和水就是傅里叶变换中的“简单标准化事物”。菜谱只需要告诉你成分即可,大家约定俗成都知道这些食材是什么。
这说明了什么?
说明如果一个社会有一个标准化的简单事物话语体系,交流会非常方便。这也意味着要想高效交流,就必须有一个约定俗成的标准化简单事物体系。
在现代社会,使用傅里叶变换的实际操作总是会有失真。
理论上,标准化简单音调数量是无限的,但实际应用中我们只能用有限数字描绘声音。这是因为不易分辨的、或者振幅特别低的音调被省略了。
因此,数字化声音会有一些限制:
1、你无法发出无法用选取的简单音调描绘的声音;
2、声音的细微之处将被忽略;
3、能传播的声音都是标准化简单声音的排列组合。
这就解释了为什么福柯说,“人类的一切知识都是通过‘话语’获得的,任何脱离‘话语’的东西都是不存在的。”
在傅里叶变换的视角下,这个世界没有新鲜事物。
例如,你做了一个梦,觉得精彩绝伦,就写成小说,认为拍成电影一定会火。
但你的编剧朋友可能会说:“这不就是《罗生门》× 0.5 + 《哈姆雷特》× 0.2 + 《侏罗纪公园》× 0.3 吗?”
他对你的剧情做了傅里叶变换。如今所有的剧情桥段都可能被拍过了,你所谓的创造,通常只是已知标准化简单事物的排列组合。
这就是为什么在成熟领域搞“纯创新”非常困难。如果该领域已经形成了独特的话语体系(即傅里叶变换),你首先要学习这个话语体系。
最后还有一个问题:
什么时候用傅立叶什么时候用拉普拉斯?
这就要说一下他们之间的差异了。
其实,傅立叶变换和拉普拉斯变换是两个重要的数学工具,它们在信号处理、系统分析和控制理论中有广泛的应用。尽管它们有很多相似之处,但它们也有一些关键的区别,适用于不同的情况。
什么时候该用哪个?傅立叶变换:
分析周期性信号或稳态信号的频率成分。
进行频谱分析、图像处理或信号过滤。
拉普拉斯变换:
分析系统的瞬态行为和动态响应。
设计和分析控制系统中的反馈控制器。
分析电路的瞬态和稳态响应。
可以看出,傅立叶变换和拉普拉斯变换都是强大的工具,适用于不同的分析场景。
傅立叶变换适合处理周期性和稳态信号,主要用于频谱分析和图像处理。
而拉普拉斯变换则更适合分析瞬态信号和动态系统,广泛应用于控制系统设计和电路分析。
了解两者的关系和区别,可以帮助我们在不同的工程和科学问题中选择合适的工具。
不过大家注意,傅立叶变换和拉普拉斯变换之间并没有前后关联,它们是不同时代,不同目的而发明的。
傅立叶是为了解决热传导问题提出的,而拉普拉斯是为了简化微分方程的求解过程而提出的。
最最后,我们走之前再看一眼傅立叶变换的公式,不然显得不尊重:
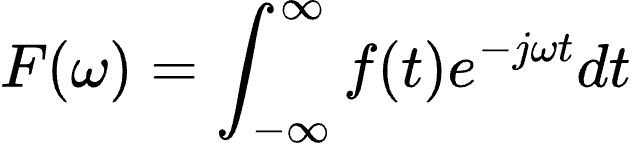
这里的,ω 是频率变量,j 是虚数单位。
结语
傅里叶变换让我们看到,即使是复杂的事物,也能拆解为一系列简单的成分。
这种思想不仅在科技和工程中应用广泛,也可以帮助我们理解世界和沟通交流。
理解傅里叶变换,不仅能提升我们解决问题的能力,更能让我们在生活中发现智慧的光芒。
当然,我们的故事并不会结束,未来章节还会慢慢细化关于这方面的知识。明天我还会给大家看一个神仙级数学宝器,敬请期待!


王大勇
一个鸡蛋用心做是可以垂直立起,但遇到轻微的干扰力就会倒下,现在如果把鸡蛋内部的液体取出来,在鸡蛋壳内立起一个陀螺仪,陀螺仪的转轴两端和鸡蛋壳固定,如果在立起鸡蛋壳时,高速启动陀螺仪,在鸡蛋壳内部陀螺高速转动的时候,在鸡蛋壳顶部给一个水平向右侧干扰力,外表静止的鸡蛋壳会先向右侧倒下,紧接着已经又立起来,有时会颠倒立起来,完全违反角动量守恒,和牛顿第二定律。给鸡蛋壳内部装一个陀螺仪是有些困难,现在网上有卖带外部框架的陀螺仪玩具,完全可以代替完成本实验。按照经典理论可以用实践验证得到陀螺效应是违反角动量守恒,和牛顿第二定律的。为什么呢?深入研究得出时空的新发现,实验和理论结果已在整理中,准备在此公开奉献给大家。
用户47xxx06
大佬们看了半天是不是看不懂?没关系,看不懂就是神,科学的尽头就是神。如把音频从wav转为MP3,用忽悠里叶变换理论套上去,瞬间变成每天都用,神就是这么伟大
我乐哈哈
不知为啥,让我想到了洛伦兹变换[笑着哭]